단면 2차 모멘트 (Moments of Inertia of Areas)

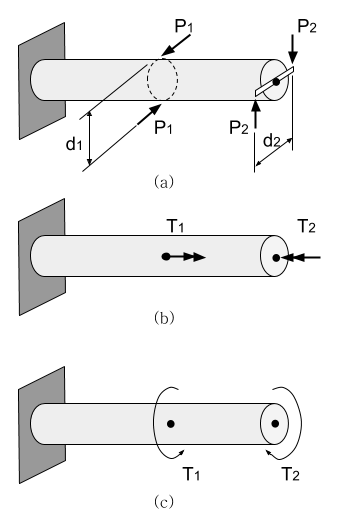
x와 y축에 대한 단면의 관성 모멘트(moments of inertia) (아래 그림 참조)는 각각 적분 \[{\rm I}_x=\int y^2d{\rm A}\qquad{\rm I}_y=\int x^2d{\rm A}\] 에 의해서 정의된다. 여기서 x와 y는 미소 면적요소 dA의 좌표이다. dA가 거리의 제곱과 곱해지기 때문에 관성 모멘트는 단면의 2차 모멘트(second moments) 라고도 불리운다. 관성 모멘트가 어떻게 적분으로 얻을 수 있는가를 설명하기 위해, 아래 그림과 같은 사각단면을 생각한다. x와 y축의 원점은 도심 에 위치하고 있다. 편의 상, 폭 b와 높이 dy의 얇은 띠 형태의 면적요소를 이용하면 dA=bdy 이다. 그러면 x축에 대한 관성 모멘트는 \[{\rm I}_x=\int_{-h/2}^{h/2}y^2bdy=\frac{bh^3}{12}\] 이다. 유사한 방법으로 세로 띠 형태의 면적요소 dA를 이용하면 y축ㅇ에 대한 관성 모멘트를 얻는다. \[{\rm I}_y=\int_{-b/2}^{b/2}x^2hdx=\frac{hb^3}{12}\] 만약 다른 축을 선택하면 관성 모멘트는 다른 값을 갖게 된다. 예를 들어, 사각형의 하단 축을 생각하자. 이 경우에는 y를 하단축으로부터 면적요소 dA까지의 거리로 정의한다. 그러면 관성 모멘트의 계산은 다음과 같다. \[{\rm I}_{bottom}=\int_0^hh^2bdy=\frac{bh^3}{3}\] 도심의 x축 보다 하단 축에 대한 관성 모멘트가 더 크다는 것에 주목한다. 일반적으로, 관성 모멘트는 기준축이 그 자신에 평행하게 도심으로부터 멀어질 수록 증가한다. 축의 선택과 무관하게 관성 모멘트는 x와 y좌표가 제곱되므로 항상 양수값을 갖는다(첫번째 식 참조). 특정 축에 대한 복합단면의 관성 모멘트는 각 부분들의 동일 축에 대한 관성 모멘트들의 합이다. 예를 들어 위의 그림 왼쪽 중공박스 단면이 있다. x축은 도심 C를 지나는 대칭 축이 된다. 이 x축에 대한 관성 모멘트는 두 사각형의 ...