기계공학 (Mechanical Engineering)

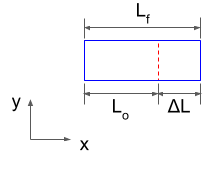
개요 (Introductions) 미소변형률(small strains)에서 실제 제약은 변형률 자체가 아니라 회전이 미소해야 한다는 것이다. 회전량이 커질 수록, 미소변형률 텐서의 정확도도 저하된다. 신장텐서(stretch tensor), 특히 U - I 는 변형률 텐서의 모든 요구 성질을 충족하고 미소 회전에 제한을 받지 않는다. 하지만 U 는 계산하기 매우 어렵기 때문에 계산이 용이하고 강체회전에 무관한 변형률 정의가 필요하다. 이 딜레마에 대한 답은 그린변형률 텐서(Green strain tensor) 이다. 그린변형률 정의 (Green Strain Definition) 그린변형률 텐서 E 는 다음과 같이 변형구배 F 로부터 정의된다. ( I 는 단위행열) \[{\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F-I}\right)\] 아래 식과 같이 \({\bf F}^T\cdot{\bf F}\)는 강체 회전 (rigid body rotation) R을 기존 변형률로부터 완전히 제거한다. \[{\bf F}^T\cdot{\bf F}=\left({\bf R}\cdot{\bf U}\right)^T\cdot({\bf R}\cdot{\bf U})={\bf U}^T\cdot{\bf R}^T\cdot{\bf R}\cdot{\bf U}={\bf U}^T\cdot{\bf U}\] 위의 결과로 계산에서 신장 텐서 U 만 남게 되어 실제로 어떠한 회전과도 독립적이다. 그린 변형률 텐서를 텐서 표기법 으로 쓰면 \(F_{ij}=\delta_{ij}+u_{i,j}\) 이므로 \[\begin{align}E_{ij}&={1\over2}\left(F_{ki}F_{kj}-\delta_{ij}\right)\\&={1\over2}\left\{\left(\delta_{ki}+u_{k,i}\right)\left(\delta_{kj}+u_{k,j}\right)-\delta_{ij}\right\}\\&={1\over2}\left(\del

This problem is a statically indeterminated truss system (Figure 1). Let us find the unknown forces of each bar by a flexibility method. Figure 1 \[x_1,\,x_2,\,x_3\ :\ \text{area of each bar, E : young's modulus}\] We cannot determine each reaction forces by static equilibrium due to lack of the number of equations. So remove the centered bar to apply the flexibility method. Then, we can get the displacement, δ (Figure 2). Figure 2 \[{\rm F'_1=P,\,F'_3=0,}\,\delta=\frac{{\rm P}l}{{\rm E}x_1\cos\theta}\] Secondly, the redundant force, \(\rm F_2\) loads the bar upward, and find the displacement, \(u_{\rm F}\) and \(v_{\rm F}\) in the horizontal and vertical direction respectively (Figure 3). W e assumed \(x_1<x_3\), Figure 3 In this case, each reaction force of bar 1 and 3, F' can be found from the equilibrium as below (Figure 4). Figure 4 \[{\rm F}'={{\rm F}_2\csc\theta\over2}\] The displacement diagram can be drawn from geometry as Figure 5. Then, we can calc

헬름홀츠 자유에너지(Helmholtz Free Energy) 헬름홀츠 자유에너지(Ψ)는 내부 에너지(u) 및 엔트로피(s)와 온도(T)의 곱, 두 상태변수의 조합이다. \[\Psi=u-Ts\] 헬름홀츠 자유에너지의 시간 증분(time increment)은 적(積)의 미분법에 의해 \[\dot\Psi=\dot u-\dot Ts-T\dot s\] 양변에 밀도 ρ를 곱하면 \[\rho\dot\Psi=\rho\dot u-\rho\dot Ts-\rho T\dot s\] 한편 열역학 제2법칙을 내부에너지, 응력 ( σ ) 및 변형률 속도 텐서(strain rate tensor)( D )로 나타내면 \[\rho T\dot s\ge\rho\dot u-\boldsymbol\sigma:\bf D\] 위의 두식을 결합하면 다음식을 얻는다. \[\boldsymbol\sigma:{\bf D}\ge\rho\dot u-\rho T\dot s=\rho\dot\Psi+\rho s\dot T\] 이제 변형률 속도 텐서는 탄성(elastic)과 비탄성(inelastic)으로 나눌 수 있다. \[{\bf D}={\bf D}_{\rm el}+{\bf D}_{\rm in}\] 탄성 부분만 응력을 발생시킨다. 비탄성 부분은 그렇제 못하다. 이는 비가역적인 영구 변형을 나타낸다. 금속에서는 소성 변형이 해당된다. 토양에서도 나타나며 거의 모든 재료에서 어느 정도 발생한다. 위의 식으로부터 \[\boldsymbol\sigma:{\bf D}_{\rm el}+\boldsymbol\sigma:{\bf D}_{\rm in}\ge\rho\dot\Psi+\rho s\dot T\] 다음 단계로 헬름홀츠 자유에너지의 구성 모델(constitutive model)을 제안한다. 요컨데, Ψ는 내부에너지(internal energy)를 포함하므로, 변형률 에너지(strain energy)가 포함되어야 하며, 따라서 그린변형률 텐서(Green strain tensor) E 의 탄성부분이 선정될 수 있다. 또한 내부에너