기계공학 (Mechanical Engineering)

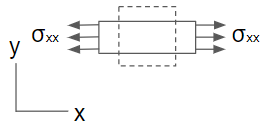
2-D 평형 (2-D Equilibrium) 아래와 같은 2차원 미소요소에 작용하는 모든 힘의 합은 ma와 같아야 한다. 요소에 작용하는 힘들은 아래와 같이 방향별 응력 성분들로 구성된다. \[\begin{split}&{\rm F}_{xx}+d{\rm F}_{xx}=\sigma_{xx}dy+\frac{\partial\sigma_{xx}}{\partial x}dxdy,\ &{\rm F}_{yy}+d{\rm F}_{yy}=\sigma_{yy}dx+\frac{\partial\sigma_{yy}}{\partial y}dxdy\\&{\rm F}_{xy}+d{\rm F}_{xy}=\tau_{xy}dy+\frac{\partial\tau_{xy}}{\partial x}dxdy,&{\rm F}_{yx}+d{\rm F}_{yx}=\tau_{yx}dx+\frac{\partial\tau_{yx}}{\partial y}dxdy\end{split}\] 또한 여기에 체적력(body force)이 더해진다. 이들은 중력, 자기력 등을 포함하며 ρfdxdy 로 나타낸다. 여기서 ρ는 밀도, f는 단위질량 당 힘이다. 먼저 x방향 힘의 평형을 생각하면 \(\sum {\rm F}_x=ma_x\) 이므로 \[\begin{align}&-{\rm F}_{xx}-{\rm F}_{yx}+{\rm F}_{xx}+d{\rm F}_{xx}+{\rm F}_{yx}+d{\rm F}_{yx}+\rho f_xdxdy=ma_x\\&\frac{\partial\sigma_{xx}}{\partial x}dxdy+\frac{\partial\tau_{yx}}{\partial y}dxdy+\rho f_xdxdy=\rho dxdya_x\end{align}\] dxdy로 양변을 나누면 \[\frac{\partial\sigma_{xx}}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}+\rho f_x=\rho a_x\] y방향에 대해서도 같은

반력(reactions)의 개수가 정적 평형(static equilibrium)의 방정식으로부터 구할 수 있는 것보다 많은 보(beam)를 부정정 (statically indeterminate) 보라 부르고, 분석을 위해서는 처짐(deflection)의 계산이 요구된다. 위의 그림에 몇가지 형태의 부정정 보가 도시되어 있다. 그림 [a]는 지지부 A에서 고정되고 B에서 단순 지지되고 있다; 이러한 보를 일단고정 타단지지 보 (propped cantilever beam or fixed simple beam)라 부른다. 보의 반력들은 A에서의 수직 및 수평력, 우력 그리고 B에서의 수직력이다. 정적 평형에 의한 독립적인 방정식이 3개 밖에 없으므로 이들 4개의 반력들을 정적으로 구하는 것은 불가능하다. 평형 방정식을 초과하는 반력의 수를 정적 부정도 (degree of statical indeterminacy)라 한다. 따라서 그림 [a]의 보는 1도의 정적 부정도를 가진다. 정적으로 결정될 수 있는 지지구조를 초과하는 반력들을 정적 잉여 (statical redundants)라고 부르며, 이러한 잉여의 수는 정적 부정도와 같다. 예를 들어 그림 [a]의 반력 Rb는 잉여 반력이라 할 수 있다. 지지부 B가 제거되면 외팔보가 되는 것에 주목한다. 이러한 잉여가 제거된 정정(statically determinate) 구조를 제거구조 (released structure) 또는 기본구조 (primary structure)라 한다. 그림 [a] 보의 다른 접근법은 반력 모멘트 Ma를 잉여로 생각하는 것이다; 이 모멘트가 제거되면, 제거구조는 부동힌지지점(pin support) A와 가동힌지지점(roller support) B를 가진 단순보가 된다. 양단고정보 (fixed ens beam or fixed-fixed beam or clamped beam)가 그림 [b]에 나타나 있다. 각 지지부에 3개의 반력 성분들을 가지고 있다; 따라서 보는 전부 미지의 반력 6개

보의 처짐을 구할 수 있는 다른 방법을 생각해 본다. 이 방법은 면적모멘트법 (moment-area method)으로 알려져 있으며, 굽힘모멘트 선도의 면적 특성을 활용한 것이다. 이 방법은 오직 보의 한 점에서의 처짐(deflection) 또는 회전각(angle of rotation)이 요구될 때 적합하다. 왜냐하면 처짐곡선(deflection curve)의 완전한 방정식을 구하지 않고 그것들을 구할 수 있기 때문이다. 1차 면적모멘트 정리 (First moment-area theorem) 위의 그림과 같이 보의 처짐곡선의 일부인 AB를 생각하자. A점에서의 접선 AB'는 x축으로부터 양의 회전각 \(\theta_a\)를, 그리고 B점에서의 접선 C'B는 \(\theta_b\)를 이루고 있다. 이 접선들 간의 각도 \(\theta_{ba}=\theta_b-\theta_a\) 이다. 다음으로 거리 ds 만큼 떨어져 있는 두 점을 생각하자. 이들 두 점의 접선에 수직한 선들은 각도 dθ=ds/ρ를 (여기서 ρ는 곡률반경) 이루는 곡률 중심(center of curvature)에 교차한다. 각도 dθ는 처짐곡선의 미분방정식으로부터 얻을 수 있다. \[d\theta=-\frac{Mdx}{EI}\] 여기서 M은 보의 굽힘모멘트이고 EI는 굽힘강성계수(flexural rigidity) 이다. Mdx/EI는 단순한 기하학적 의미를 가진다. 위의 그림의 보 바로 아래 M/EI 선도가 그려져 있다. Mdx/EI 항은 M/EI 선도 내의 음영으로 된 띠의 면적이 된다. 이제 위의 식을 A점에서 B점까지 적분 해보자 : \[\theta_{ba}=\theta_b-\theta_a=\int_A^Bd\theta=-\int_A^B\frac{Mdx}{EI}\] 이 적분의 좌변은 B와 A 접선 사이의 상대 각도이다. 우변은 A와 B점 사이의 M/EI 선도의 면적과 같다. 이 방정식을 1차 면적모멘트 정리 (first moment-area theorem)라 한다. 2차

개요 (Introduction) 후크의 법칙은 선형 정방성(linear and isotropic)이다. 사실 이 법칙은 정방성이라면 비선형을 포함한 초탄성(hyperelastic) 재질의 1차 선형(1st order linearization)이라 할 수 있다. 따라서 변형률이 작다면 고무에도 적용할 수 있다. 금속의 탄성영역에서는 표준 법칙이다. 수직 성분 (Normal Component) 전체 모델을 얻기 위한 첫번째 단계는 단순 인장/압축으로 출발한다. 이 경우 응력-변형률 관계는 \(\sigma=E\epsilon\) 응력 및 변형률 항이 모두 1차식으므로 선형이다. 변형률은 단위가 없으므로 E는 σ와 같이 응력의 단위를 가진다. 다음 단계는 다차원으로 일반화 하는 것이다. 먼저 인장/압축의 방향을 x라 하자. 그러면 위의 식을 다음과 같이 쓸 수 있다. \[\epsilon_{xx}={1\over E}\sigma_{xx}\] 이제 y 방향 수직응력을 추가 한다. y 방향 인장 응력은 x 방향 변형률을 감소시킨다. 따라서 위의 식을 아래와 같이 변화시킨다. \[\epsilon_{xx}={1\over E}\sigma_{xx}-B\sigma_{yy}={1\over E}\sigma_{xx}-\nu{1\over E}\sigma_{yy}\] 이 경우 B는 E 처럼 물성치이고 실험으로 결정된다. 하지만 B를 이 형태로 쓰는 것은 실용적이지 않다. 1/E에 대한 비율로 표현하는 것이 훨씬 유용하다.  이 비율을 ν로 나타내며 포아송 비(poisson's ratio) 라고 한다. 이것은 응력 방향과 그것에 수직 방향에 대한 변형률의 민감도 비율이다. 만약 재질이 정방석이면 \(\sigma_{zz}\)에 대한 \(\epsilon_{xx}\)의 응답은 \(\sigma_{yy}\)와 같다. 따라서 위의 식은 다음과 같이 쓸 수 있다. \[\epsilon_{xx}={1\over E}\left\{\sigma_{xx}-\nu\left(\sigma_{yy}+\sigma

개 요 (Introduction) 회전 행열 R 은 3-D 공간에서 물체의 회전을 표현한다. 이것은 변형구배 (deformation gradients)와 극좌표분해(polar decomposition)에서 소개된 바 있다. 회전 행열은 좌표변환 행열 Q 와는 다르지만 밀접하게 관련이 있다. 변환 행열 은 물체를 고정한 채 좌표계의 변환만을 나타낸다. 반면에 회전 행열은 고정된 좌표계에서 물체의 회전을 표현한다. 종종 혼란스럽기도 하지만, 놀라운 사실은 각 행열은 다른 행열에 대해서 전치(tranpose) 행열이라는 것이다. 요 약 (Summary) 회전 행열 R 은 좌표계는 고정하고 벡터 와 텐서를 회전시키는데 쓰인다. 물체가 회전될 때 통상 이 물체와 관련된 벡터와 텐서도 같이 회전하게 된다. 회전 행열을 적용하는 일반적인 규칙은 좌표변환 행열(coordinate transformation matrix)과 동일하다. 벡터(Vectors)                               \({\bf v'}={\bf R}\cdot{\bf v}\) 2등급 텐서(2nd Rank Tensors) \(\boldsymbol\sigma'={\bf R}\cdot\boldsymbol\sigma\cdot{\bf R}^T\) 2등급 텐서(4th Rank Tensors) \({\bf C'}={\bf R}\cdot{\bf R}\cdot{\bf C}\cdot{\bf R}^T\cdot{\bf R}^T\) 그리고 텐서 표기법 (tensor notation)으로는 벡터            \(v'_i=R_{ij}v_j\) 2등급 텐서 \(\sigma'_{mn}=R_{mi}R_{nj}\sigma_{ij}\) 4등급 텐서 \(C'_{mnop}=R_{mi}R_{nj}R_{ok}R_{pl}C_{ijkl}\) 2차원에서 R 은 \({\bf R}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&a