기계공학 (Mechanical Engineering)

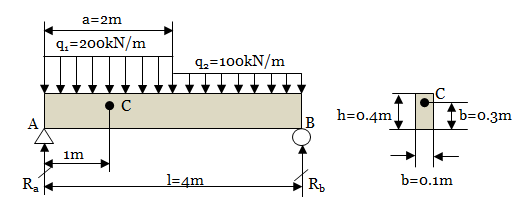
1. 다음 그림과 같이 직사각형 단면의 단순지지 보가 분포하중을 받고 있다. 이 때, C점에서의 굽힘응력 과 전단응력 을 구하라. <풀이> 지지점 A, B에서의 모멘트 평형 으로부터 \[R_a={a\over4}(3q_1+q_2)=350\ {\rm kN}\qquad R_b={a\over4}(q_1+3q_2)=250\ {\rm kN}\] 구간 [0, a]에서 A로부터 거리 x 위치의 모멘트식으로부터 C점의 위치, x=1m에서의 모멘트 M을 구할 수 있다. \[M(x)={x\over2}(2R_a-q_1x)\qquad M(1)=250\ {\rm kNm}\] 따라서 C점, 즉 y=-0.1m 에서의 굽힘응력 σ는 다음과 같다. 여기서 I는 단면 2차 모멘트 이다. \[I={bh^3\over12}=0.00333\ {\rm m^4}\qquad\sigma={My\over I}=-7,5000\ {\rm kN/m^2}\] 다음으로 구간 [0, a]에서 거리 x 위치의 전단력식으로부터 C점의 전단력 V를 구한다. \[V(x)=R_a-q_1x\qquad V(1)=150\ {\rm kN}\] 이로부터 C점에서의 전단응력 τ를 구한다. \[\tau={V\over bh}=3,750\ {\rm kN/m^2}\] 2. 두께가 20mm 인 Bottom Shell의 굽힘감도 보강을 위해 Built-Up T-bar를 부착하여 보강판 구조를 만들고자 한다. 구조 강도를 검토한 결과, 보강재 개당 탄성 단면계수 1600 cm³, 전단면적 70 cm² 이 요구되었다. 보강재의 구조적 거동에 기여하는 판의 효과를 고려하여 Built-Up T-bar의 최적단면을 설계하라. (보강재 웨브의 두께 : \(t_w=12\ {\rm mm}\)) <풀이> 아래 그림과 같이 T-bar의 치수를 B, H로 두고 문제의 조건을 만족하는 치수를 찾는다. 보강재 개당 면적 A=7,000 mm ² 이므로 \[A=t_w(B+H)=7,000\ {\rm mm^2}\] 이다. 이 식으로부터 B, H

1. 다음식으로 정의된 함수 f의 정의역과 치역을 구하여라. \((1)\ f(x)={1\over1+x}\qquad(2)\ f(x)={1\over1+x^2}\qquad(3)\ f(x)={1\over1+\sqrt{x}}\qquad(4)\ f(x)=x^3-3x+2\\(5)\ f(x)=\sqrt{x^2-2x-3}\qquad(6)\ f(x)=\sqrt{x(x-1)(x-2)}\qquad(7)\ f(x)={2x+3\over x+2}\) <풀이> \((1)\ 1+x\ne0\ 이어야\ 하므로\ D_f=\{x\in R|x\ne-1\},\,\lim_{x\to\pm\infty}f(x)=0\ 이므로\\\quad\ \ R_f=\{y\in R|y\ne0\}\\(2)\ D_f=(-\infty,\infty),\,x^2\ge0\ 이므로\ R_f=(0,1]\\(3)\ D_f=[0,\infty),\,\lim_{x\to\infty}f(x)=0\ 이므로\ R_f=(0,1]\\(4)\ D_f=(-\infty,\infty),\,f(x)=(x-2)(x-1)에서\ 최소값\ f({3\over2})=-{1\over4}\ 이므로\ R_f=[-{1\over4},\infty)\\(5)\ (x-3)(x+1)\ge0\ 이므로\ D_f=(-\infty,-1]\cup[3,\infty),\,R_f=[0,\infty)\\(6)\ x(x-1)(x-2)\ge0\ 이므로\ D_f=[0,1]\cup[2,\infty),\,R_f=[0,\infty)\\(7)\ x+2\ne0\ 이므로\ D_f=\{x\in R|x\ne-2\},\,f(x)=2-{1\over x+2}\ne2\ 따라서\\\quad \ R_f=\{y\in R|y\ne2\}\) 2. 실수 a, b에 대하여 작지 않은 것은 max{a, b}, 크지 않은 것은 min{a, b}라 할 때 다음이 성립함을 보여라. \[\max\{a,b\}=\frac{a+b+|a-b|}{2},\,\min\{a,b\}=\frac{a+b-|a-b|}{2}\] <풀이> \(a\

두 벡터의 다이애딕곱(Diadic product)은 텐서(혹은 행열)을 반환하며 아래와 같이 정의한다. \[{\bf a}\otimes{\bf b}=(a_1,a_2,a_3)\otimes(b_1,b_2,b_3)=\begin{bmatrix}a_1b_1&a_1b_2&a_1b_3\\a_2b_1&a_2b_2&a_2b_3\\a_3b_1&a_3b_2&a_3b_3\end{bmatrix}\] 텐서표기법 으로는 \[a_i\otimes b_j=a_ib_j\]

유체역학(流體力學)은 유체가 정지상태에 있거나 운동상태에 있을 때 여러가지 조건 아래서의 역학적 관계를 연구하는 학문이다. 구체적으로 공기나 물 또는 그 밖의 유체를 작동매체로 하는 유체기계에서는 물론, 조선, 항공, 토목, 건축, 화공, 원자력, 광산, 전기 등 거의 모든 공학분야에 유체에 관련된 이론과 실제 문제에 관한 정보를 제공한다. 유체역학은 이상유체(理想流體)를 대상으로 응용수학이나 물리적 측면에서 보는 이론유체역학(hydrodynamics)과 물이나 그 밖의 실제유체(實際 流體 )를 경험적 관점에서 보는 수력학(hydraulics)의 두 갈래가 있지만 이들을 묶어 유체역학(fluid mechanics)이라는 하나의 테두리 안에서 다루는 것이 보편화되어 있다. 고대 그리스의 철학자 엠페도클레스(Empedokles, 483~435 B.B.)는 만물이 흙, 물, 공기, 불의 네가지 요소로 구성되었다고 주장하였다. 이는 물질이 4가지 상태, 즉 고체(solid) , 액체(liquid) , 기체(gas) , 프라즈마(plasma) 로 존재할 수 있다는 사실과 일치한다. 프라즈마란 물질을 구성하는 대부분의 분자들이 이온(ion)화된 상태를 말한다. 따라서 전기적 성질을 띤 입자들을 포함하고 있으므로 전자기력을 받을 수 있다. 물질을 구성하는 분자들의 운동에너지는 고체에서 액체, 기체, 프라즈마 상태로 갈 수록 커진다. 이 중 액체, 기체, 프라즈마를 통틀어서 유체(fluid) 라고 한다. 그러나 일상적으로 접하는 물질들 중에, 불을 제외하고 프라즈마로 존재하는 물질은 거의 없으므로, 일반적으로 유체는 액체와 기체의 두가지 상태로 나누어진다고 생각하는 것이 편리하다. 액체는 유한한 체적을 갖기 때문에 일정량의 액체를  밀폐된 용기 속에 넣었을 때 일정한 공간만을 차지하고 표면을 갖는 반면에, 기체는 용기의 체적에 관계없이 주어진 공간을 모두 차지한다. 이는 분자들 간에 작용하는 응집력의 차이에 기인한다. 액체는 기체보다 응집력이 크게 작용하게 때문에 뚜