기계공학 (Mechanical Engineering)

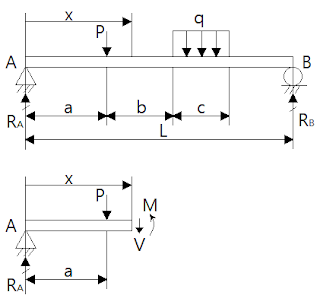
보의 전단력과 굽힘모멘트 (Shear Force and Bending Moment in Beam) 보(beam)의 임의의 위치 단면에서의 전단력과 굽힘모멘트를 구해 보자. 이것은 보에 작용하는 응력 의 합력(resultants)으로 발생한 것이다. 아래와 같이 단순보(simple beam)와 좌단에서 x 만큼 떨어진 단면으로 자른 자유체(free body)를 생각한다. 먼저 지지부의 반력을 구한다. 정정보(statically determinate beam)이므로 평형 방정식으로 구할 수 있다. 지지부 A에서의 모멘트 평형(\(\sum \text{M}=0\))으로부터 \(\begin{gather}\text{R}_\text{A}-\text{P(L}-a)-qc\left(\text{L}-a-b-{c\over 2}\right)=0\\\therefore\;\text{R}_\text{A}={1\over \text{L}}\left\{\text{P(L}-a)+qc\left(\text{L}-a-b-{c\over 2}\right)\right\}\end{gather}\) 또한 \(\sum\text{F}_\text{y}=0\) 이므로 \(\text{R}_\text{B}=\text{P}+qc-\text{R}_\text{A}={1\over \text{L}}\left\{\text{P}a+qc\left(a+b+{c\over 2}\right)\right\}\) 이제 x 위치의 단면에서의 전단력을 동일한 방법으로 자유체에서 평형 방정식을 적용하여 구한다. \(a<x\leq(a+b)\) 구간을 예로 들면 \(\text{V}=\text{R}_\text{A}-\text{P}={1\over\text{L}}\left\{-\text{P}a+qc\left(\text{L}-a-b-{c\over 2}\right)\right\}\) 동일하게 모멘트 평형으로부터 \(\text{M}+\text{P}(x-a)-\text{R}_\text{A}x=0\) 단면의 모멘트 M은 x에 대한 1차 함수가 된다. \

상당 응력(von Mises stress)은 종종 복합하중을 받는 정방성 , 연성 금속의 항복 여부를 판단하는데 쓰인다. 상당 응력을 계산한 후 재료의 항복응력과 비교함으로서 이루어지는 데 이를 von Mises Yield Criterion (항복조건)이라 한다. 그 목적은 수직/전단 응력 의 조합과 상관없이, 복합 3-D 하중 조건하에서 연성 금속의 항복 조건(yield criterion)을 전개하는데 있다. 상당 응력은 복합 응력 상태를 단일 스칼라 값으로 변환하고 이를 실험실에서 재료의 단축인장 시험으로부터 결정된 (이 역시) 단일 스칼라 값인 항복강도(yield strength)와 비교함으로써 가능케 한다. 이는 정확한 과학이라기 보다는 오차와 편차를 내재한 실험적인 과정임을 유의해야 한다. 사실 금속이 반드시 von Mises yield criterion에 따라 항복한다고 단정할 수는 없다. 하지만 처음 제안된 이후 세기에 걸처 선택할 수 있는 방법의 하나로 사용되고 있다. 역사 상당 응력의 정의는 1904년 Huber가 처음 제안하였으나 1913년 von Mises가 다시 제안할 때 까지는 그다지 주목 받지 못하였다. 그러나 Huber와 von Mises의 정의는 물리적 의미가 없는, 단지 수학적인 것 이었으나 1924년 Hencky가 편향 변형률에너지(deviatoric strain energy) 와 관련이 있다는 것을 알아냈다. 1931년 Taylor와 Quinney는 구리, 알루미늄 및 연강이 1864년 Tresca가 제안한 최대 전단응력 조건(maximum shear stress criterion) 보다 금속의 항복을 더 정확히 예측하는 시험 결과를 발표하였고 오늘날까지 금속 항복 예측의 최선의 방법으로 여겨지고 있다. 정수압과 편향 성분(Hydrostatic and Deviatoric Components) 응력 텐서는 정수압과 편향 응력 의 합으로 다음과 같이 분해된다. \(\sigma_{ij}={1 \over3} \delta_{i