전단력과 굽힘모멘트 (Shear Force and Bending Moment)

보의 전단력과 굽힘모멘트 (Shear Force and Bending Moment in Beam)

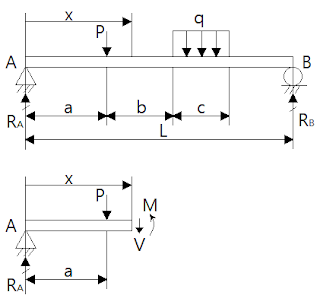
보(beam)의 임의의 위치 단면에서의 전단력과 굽힘모멘트를 구해 보자. 이것은 보에 작용하는 응력의 합력(resultants)으로 발생한 것이다. 아래와 같이 단순보(simple beam)와 좌단에서 x 만큼 떨어진 단면으로 자른 자유체(free body)를 생각한다.

먼저 지지부의 반력을 구한다. 정정보(statically determinate beam)이므로 평형 방정식으로 구할 수 있다. 지지부 A에서의 모멘트 평형(\(\sum \text{M}=0\))으로부터

\(\begin{gather}\text{R}_\text{A}-\text{P(L}-a)-qc\left(\text{L}-a-b-{c\over 2}\right)=0\\\therefore\;\text{R}_\text{A}={1\over \text{L}}\left\{\text{P(L}-a)+qc\left(\text{L}-a-b-{c\over 2}\right)\right\}\end{gather}\)

또한 \(\sum\text{F}_\text{y}=0\) 이므로

\(\text{R}_\text{B}=\text{P}+qc-\text{R}_\text{A}={1\over \text{L}}\left\{\text{P}a+qc\left(a+b+{c\over 2}\right)\right\}\)

이제 x 위치의 단면에서의 전단력을 동일한 방법으로 자유체에서 평형 방정식을 적용하여 구한다. \(a<x\leq(a+b)\) 구간을 예로 들면

\(\text{V}=\text{R}_\text{A}-\text{P}={1\over\text{L}}\left\{-\text{P}a+qc\left(\text{L}-a-b-{c\over 2}\right)\right\}\)

동일하게 모멘트 평형으로부터

\(\text{M}+\text{P}(x-a)-\text{R}_\text{A}x=0\)

단면의 모멘트 M은 x에 대한 1차 함수가 된다.

\(\text{M}={x\over\text{L}}\left\{-\text{P}a+qc\left(\text{L}-a-b-{c\over 2}\right)\right\}+\text{P}a\)

단면의 방향에 따라 전단력과 모멘트의 부호를 일관성 있게 나타내기 위하여 다음과 같이 부호 규약(sign conventions)을 따른다.

하중, 전단력 및 굽힘 모멘트 간의 관계 (Relation between Load, Shear Force and Bending Moment)

전체 보의 전단력과 모멘트를 조사하기 위해 이들과 하중과의 관계를 아는 것은 꽤 유용하다. 거리가 \(dx\)인 빔 요소를 가정하고 좌단에 양의 방향으로 전단력 V와 굽힘 모멘트 M이 작용한다고 한다. V와 M은 x의 함수이므로 우단은 각각 \(\text{V}+d\text{V}\), \(\text{M}+d\text{M}\)으로 나타낼 수 있다. 그리고 상단에 분포하중 q가 가해진다고 하자.

수직 방향 힘의 평형으로부터

\(\text{V}-(\text{V}+d\text{V})-qdx=0\quad\therefore\:\frac{d\text{V}}{dx}=-q\)

전단력 V는 x축을 따라 -q의 기울기로 변화한다. 또한 분포하중이 없으면 전단력의 변화는 없다.

다시 요소의 모멘트 총합의 평형을 생각하고 미소항을 무시하면 다음 식을 얻는다.

\(-\text{M}-qdx\left({dx\over 2}\right)-(\text{V}+d\text{V})dx+\text{M}+d\text{M}=0\quad\therefore\:\frac{d\text{M}}{dx}=\text{V}\) 

위의 식은 M의 변화율은 V와 같다는 것을 나타낸다. 이 식은 분포하중일 경우만 적용되므로 집중하중이 있는 구간에서는 정의될 수 없다.

전단력 및 굽힘 모멘트 선도 (Shear Force and Bending Moment Diagram)

빔 설계에 있어서 모든 구간에서 단면에 작용하는 V, M을 파악하는 것이 요구된다. 편리한 방법으로 단면의 위치를 x축으로, V 또는 M의 값을 y축으로 그래프를 그리면 된다. 이들의 전단력과 굽힘 모멘트 선도이다.

1개의 집중하중(concentrated load)을 받는 단순보(simple beam)를 생각하자.

모멘트와 수직 방향 힘의 평형으로부터 반력을 구하면 다음과 같다.

\(-\text{R}_\text{A}\text{L}+\text{P}b=0,\,\text{R}_\text{A}=\frac{\text{P}b}{\text{L}},\,\text{R}_\text{B}=\text{P}-\text{R}_\text{A}=\frac{\text{P}a}{\text{L}}\)

구간 \(0<x\leq a\)에서 자유체의 평형으로부터

\(\text{V}=\text{R}_\text{A}=\frac{\text{P}b}{\text{L}},\,\text{M}=\text{R}_\text{A}x=\frac{\text{P}bx}{\text{L}}\)

마찬가지로 구간 \(a<x\leq\text{L}\)에서 빔의 좌측 또는 우측부분의 평형을 고려하면

\(V=\frac{\text{P}b}{\text{L}}-\text{P},\,\text{M}=\frac{\text{P}bx}{\text{L}}-\text{P}(x-a)=\text{P}a\left(1-{x\over\text{L}}\right)\)

이제 구간별 위의 식들로부터 V, M의 전체 선도를 완성하면 위의 그림과 같다. 전단력은 구간별로 일정하며 모멘트는 x=a에서 최대값 \(\text{P}ab/\text{L}\)을 가진다.

전단력 선도에서 \(d\text{V}/dx=0\) 이다. 왜냐하면 \(d\text{V}/dx=-q\) 인데 분포하중 q=0 이기 때문이다. 또한 굽힘 모멘트 M의 기울기 \(d\text{M}/dx\)는 그 구간의 전단력 V와 같음을 알 수 있다. 집중하중 P의 작용점에서는 전단력의 급격한 변화가 일어나며 그 크기는 P와 같다.

아래는 균일 분포하중(uniformly distributed load)을 받는 단순보이다. 이 경우 반력은 대칭이므로 \(\text{R}_\text{A}=\text{R}_\text{B}=q\text{L}/2\) 이다.

좌단 A로부터 거리 x 만큼 떨어진 단면의 전단력 V와 굽히 모멘트 M은 다음과 같다.

\(-\frac{q\text{L}}{2}+qx+\text{V}=0,\quad \text{V}=\frac{q\text{L}}{2}-qx\)

\(\text{M}+qx\left({x\over 2}\right)-\frac{q\text{L}}{2}x=0,\quad\text{M}=\frac{q\text{L}}{2}x-{q\over2}x^2\)

위의 식에서 전단력 선도는 -q의 기울기를 갖고 x=0, x=L에서 각각 \(q\text{L}/2,\,-q\text{L}/2\)의 값을 갖는 사선임을 알 수 있다(\(d\text{V}/dx=-q\) 이므로 예상과 같다). 굽힘 모멘트 선도는 좌우 대칭 포물선이며 기울기의 변화는 전단력과 같다.

\(\frac{d\text{M}}{dx}=\frac{q\text{L}}{2}-qx=\text{V}\)

최대 굽힘 모멘트 지점은 \(d\text{M}/dx=0\)가 되는 점이며 위의 예제에서는 중앙이 된다. \(x=\text{L}/2\)에서 M으로 다음을 얻는다.

\(\text{M}_{\text{max}}=\frac{q\text{L}^2}{4}-\frac{q\text{L}^2}{8}=\frac{q\text{L}^2}{8}\)

만약 아래와 같이 다수의 집중하중이 작용하는 단순보라면 각 하중점 사이 구간마다 V와 M을 결정한다.

먼저 수직하중과 모멘트 평형으로부터 지지부 반력을 계산한다.

\(-\text{R}_\text{B}\text{L}+\text{P}_1a_1+\text{P}_2a_2+\text{P}_3a_3=0,\,\text{R}_\text{B}={1\over\text{L}}(\text{P}_1a_1+\text{P}_2a_2+\text{P}_3a_3)\)

\(\text{R}_\text{A}=\text{P}_1+\text{P}_2+\text{P}_3-\text{R}_\text{B}={1\over\text{L}}\left\{\text{P}_1(\text{L}-a_1)+\text{P}_2(\text{L}-a_2)+\text{P}_3(\text{L}-a_3)\right\}\)

구간 \(0<x<a_1\)에서

\(\text{V}=\text{R}_\text{A},\quad\text{M}=\text{R}_\text{A}x\)

구간 \(a_1<x<a_2\)에서

\(\text{V}=\text{R}_\text{A}-\text{P}_1,\quad\text{M}=(\text{R}_\text{A}-\text{P}_1)x+\text{P}_1a_1\)

구간 \(a_2<x<a_3\)에서는 우단부를 고려하는 것이 하중 개수가 적으므로 편리하다.

\(\text{V}=-\text{R}_\text{B}+\text{P}_3,\quad\text{M}=(\text{P}_3-\text{R}_\text{B})x+(\text{R}_\text{B}-\text{P}_3)\text{L}+\text{P}_3b_3\)

구간 \(a_3<x<L\)에서

\(\text{V}=-\text{R}_\text{B},\quad\text{M}=\text{R}_\text{B}(\text{L}-x)\)

위의 식들에서 전단력은 각 구간에서 일정함을 알 수 있다. 또한 굽힘 모멘트는 구간마다 x의 선형함수로서 사선으로 표현된다. 각 하중 지점의 굽힘 모멘트값은 위의 각 해당구간 식에서 \(x=a_1, a_2\) 및 \(a_3\)를 대입하여 계산한다.

\(\text{M}_1=\text{R}_\text{A}a_1,\;\text{M}_2=\text{R}_\text{A}a_2-\text{P}_1(a_2-a_1),\;\text{M}_3=\text{R}_\text{B}b_3\)

각 집중하중점에서는 전단력 선도가 그 지점의 하중값 만큼 급격히 변함에 유의한다. 더우기 전단력의 불연속점에서는 굽힘 모멘트 선도의 경사, \(d\text{M}/dx\)도 그에 상당하게 변한다. 또한 구간 사이의 굽힘 모메트값 차이는 해당 구간 전단력 선도의 면적과 같다. 예를 들면 하중 P1과 P2 사이의 경우 굽힘 모멘트 차이는

\(\text{M}_2-\text{M}_1=\int_{a_1}^{a_2}Vdx=(\text{R}_\text{A}-\text{P}_1)(a_2-a_1)\)

전단력 값이 부호가 \(x=a_2\)에서 바뀌므로 최대 굽힘 모멘트는 M2가 된다. 일반적으로 최대 굽힘 모멘트 절대치는 전단력의 부호가 바뀌는 집중하중점, 반력 작용점, 전단력이 '0'이 되는 점, 또는 우력(couple) 작용점이다.