그린 변형률 (Green Strains)
미소변형률(small strains)에서 실제 제약은 변형률 자체가 아니라 회전이 미소해야 한다는 것이다. 회전량이 커질 수록, 미소변형률 텐서의 정확도도 저하된다.
신장텐서(stretch tensor), 특히 U-I 는 변형률 텐서의 모든 요구 성질을 충족하고 미소 회전에 제한을 받지 않는다. 하지만 U 는 계산하기 매우 어렵기 때문에 계산이 용이하고 강체회전에 무관한 변형률 정의가 필요하다. 이 딜레마에 대한 답은 그린변형률 텐서(Green strain tensor) 이다.
그린변형률 정의 (Green Strain Definition)
그린변형률 텐서 E는 다음과 같이 변형구배 F로부터 정의된다. (I는 단위행열)
\[{\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F-I}\right)\]
아래 식과 같이 \({\bf F}^T\cdot{\bf F}\)는 강체 회전(rigid body rotation) R을 기존 변형률로부터 완전히 제거한다.
\[{\bf F}^T\cdot{\bf F}=\left({\bf R}\cdot{\bf U}\right)^T\cdot({\bf R}\cdot{\bf U})={\bf U}^T\cdot{\bf R}^T\cdot{\bf R}\cdot{\bf U}={\bf U}^T\cdot{\bf U}\]
위의 결과로 계산에서 신장 텐서 U 만 남게 되어 실제로 어떠한 회전과도 독립적이다.
그린 변형률 텐서를 텐서 표기법으로 쓰면 \(F_{ij}=\delta_{ij}+u_{i,j}\) 이므로
\[\begin{align}E_{ij}&={1\over2}\left(F_{ki}F_{kj}-\delta_{ij}\right)\\&={1\over2}\left\{\left(\delta_{ki}+u_{k,i}\right)\left(\delta_{kj}+u_{k,j}\right)-\delta_{ij}\right\}\\&={1\over2}\left(\delta_{ki}\delta_{kj}+\delta_{ki}\delta_{k,j}+\delta_{kj}u_{k,i}+u_{k,i}u_{k,j}-\delta_{ij}\right)\\&={1\over2}\left(u_{i,j}+u_{j,i}+u_{k,i}u_{k,j}\right)\end{align}\]
위의 식을 좀 더 외연적으로 쓰면 다음과 같다.
\[E_{ij}={1\over2}\left(\frac{\partial u_i}{\partial X_j}+\frac{\partial u_j}{\partial X_i}+\frac{\partial u_k}{\partial X_i}+\frac{\partial u_k}{\partial X_j}\right)\]
이 변형률 텐서는 대칭이므로
\[{\bf E}=\begin{bmatrix}E_{xx}&E_{xy}&E_{xz}\\E_{xy}&E_{yy}&E_{yz}\\E_{xz}&E_{yz}&E_{zz}\end{bmatrix}\]
그린 변형률 텐서의 각 성분별 표현은 아래와 같다. u=(u, v, w) 임을 기억한다.
\[\begin{align}E_{xx}&=\frac{\partial u}{\partial X}+{1\over2}\left\{\left(\frac{\partial u}{\partial X}\right)^2+\left(\frac{\partial v}{\partial X}\right)^2+\left(\frac{\partial w}{\partial X}\right)^2\right\}\\E_{yy}&=\frac{\partial v}{\partial Y}+{1\over2}\left\{\left(\frac{\partial u}{\partial Y}\right)^2+\left(\frac{\partial v}{\partial Y}\right)^2+\left(\frac{\partial w}{\partial Y}\right)^2\right\}\\E_{zz}&=\frac{\partial w}{\partial Z}+{1\over2}\left\{\left(\frac{\partial u}{\partial Z}\right)^2+\left(\frac{\partial v}{\partial Z}\right)^2+\left(\frac{\partial w}{\partial Z}\right)^2\right\}\\E_{xy}&={1\over2}\left(\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial X}\right)+{1\over2}\left(\frac{\partial u}{\partial X}\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial X}\frac{\partial v}{\partial Y}+\frac{\partial w}{\partial X}\frac{\partial w}{\partial Y}\right)\\E_{yz}&={1\over2}\left(\frac{\partial v}{\partial Z}+\frac{\partial w}{\partial Y}\right)+{1\over2}\left(\frac{\partial u}{\partial Y}\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial Y}\frac{\partial v}{\partial Z}+\frac{\partial w}{\partial Y}\frac{\partial w}{\partial Z}\right)\\E_{zx}&={1\over2}\left(\frac{\partial w}{\partial X}+\frac{\partial u}{\partial Z}\right)+{1\over2}\left(\frac{\partial u}{\partial Z}\frac{\partial u}{\partial X}+\frac{\partial v}{\partial Z}\frac{\partial v}{\partial X}+\frac{\partial w}{\partial Z}\frac{\partial w}{\partial X}\right)\end{align}\]
이 방정식의 역학적 의미는 회전에 대해 독립적이다는 것이고 각 성분(component)들은 다음과 같이 나눌 수 있다.
그린 변형률(Green Strain)=미소 변형률항(Small Strain Terms)+2차항(Quadratic Terms)
미소 변형률항은 공학변형률(engineering strain)이 요구되는 특성을 가지고 있다. 2차항은 그린 변형률에 자신의 회전에 대한 독립성을 부여한다. 하지만 여기에는 대가가 있다. 변형률이 크면 2차항에 의해 미소 변형률항이 영향을 받는다.
| 전단항 주의(Shear Term Alert) 전단항은 변형률 텐서의 성분이므로 공학 전단변형률(engineering shear value)의 반이라는 것을 잊지 말아야 한다. |
U-I, 미소 변형률(Small Strain), 그린 변형률(Green Strain)
아래 변형구배 F가 주어져 있다. 그리고 극좌표분해(polar decomposition)를 하면 회전축 p=(-0.0404, -0.3539, -0.8859)를 중심으로 25˚ 강체회전(rigid body rotation)을 포함하고 있다.
\[{\bf F}=\begin{bmatrix}1&0.495&0.5\\-0.333&1&-0.247\\0.959&0&1.5\end{bmatrix}\]
회전행열(rotation matrix) R과 신장텐서(stretch tensor) U는 (F=R·U)
\[{\bf R}=\begin{bmatrix}0.903&0.378&-0.140\\-0.368&0.925&0.045\\0.158&0.011&0.986\end{bmatrix}\qquad{\bf U}=\begin{bmatrix}1.195&0.078&0.779\\0.078&1.113&-0.024\\0.779&-0.024&1.396\end{bmatrix}\]
미소 변형률 텐서 \(\boldsymbol\epsilon={1\over2}\left({\bf F}+{\bf F}^T\right)-{\bf I}\)와 \({\bf U}-{\bf I}\)는
\[\boldsymbol\epsilon=\begin{bmatrix}0.000&0.081&0.730\\0.081&0.000&-0.124\\0.730&-0.124&0.500\end{bmatrix}\qquad{\bf U}-{\bf I}=\begin{bmatrix}0.195&0.078&0.779\\0.078&0.113&-0.024\\0.779&-0.024&0.396\end{bmatrix}\]
그린 변형률 텐서 \({\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F}-{\bf I}\right)\)는
\[{\bf E}=\begin{bmatrix}0.525&0.081&1.010\\0.081&0.123&0.000\\1.010&0.000&0.781\end{bmatrix}\]
이것은 미소 변형률 텐서 ε과 U-I 와는 모두 다르다. 그러나 ε는 회전이 수반되면 변하지만, 최소한 E는 그렇지 않다. 이러한 특성은 E의 2차항에 기인한 것이다. 이로서 회전은 제거되었으나, 이 대가로 변형률이 커지면 변형률 성분에서 요구되는 공학 변형률\((\Delta L/L_o)\) 값이 변하게 된다.
미소 변형률 예 (A Smaller Strain Example)
회전은 여전히 크지만 변형률 수준이 작은 경우를 예로 들어본다. 사실은, 위의 예시와 동일한 회전행열을 쓸 것이다. 아래의 변형구배로부터 출발한다.
\[{\bf F}=\begin{bmatrix}1.0098&0.4758&-0.0445\\-0.3601&1.1001&0.1652\\0.2705&0.1687&1.3012\end{bmatrix}\]
회전행열 R은 여전히 25˚ 회전에 해당하고, 신장텐서 U는 다음과 같다.
\[{\bf R}=\begin{bmatrix}0.903&0.378&-0.140\\-0.368&0.925&0.045\\0.158&0.011&0.986\end{bmatrix}\qquad{\bf U}=\begin{bmatrix}1.10&0.05&0.10\\0.05&1.20&0.15\\0.10&0.15&1.30\end{bmatrix}\]
그린 변형률 텐서 \({\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F}-{\bf I}\right)\)는
\[{\bf E}=\begin{bmatrix}0.102&0.064&0.122\\0.064&0.221&0.187\\0.122&0.187&0.347\end{bmatrix}\]
이번에는 그린 변형융 텐서와 U-I가 ε, 특히 \(\epsilon_{11}\)과 \(\epsilon_{22}\) 성분, 보다 훨씬 서로 근접한 값을 갖는다. 이것은 변형률이 여전히 회전이 존재하지만 보다 완만한 수준이기 때문이다. 미소한 변형률에 대해서는, ε는 아니지만, 그린 변형률 텐서와 U-I는 회전 수준과 무관하게 서로 근접하게 된다.
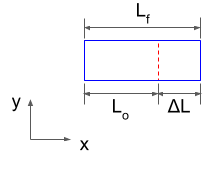
단축 인장 (Uniaxial Tension)
\[\epsilon_{xx}=\frac{\partial u}{\partial X}=\frac{\Delta L}{L_o}=\epsilon_{\rm Eng}\]
이 경우는, 그린 변형률 텐서의 영이 아닌 성분은 \(E_{11}\) 뿐이다. ∂u/∂X를 제외한 모든 편미분은 영이다. 이로부터 다음식을 얻는다.
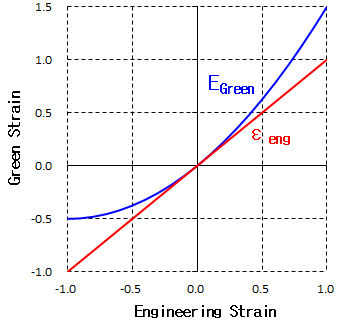
\[E_{xx}=\frac{\partial u}{\partial X}+{1\over2}\left(\frac{\partial u}{\partial X}\right)^2=\frac{\Delta L}{L_o}+{1\over2}\left(\frac{\Delta L}{L_o}\right)^2\]
그린 변형률의 절충점은 변형률이 미소할 때는 무시할 수 있는 2차항이 있고, 이것은 변형률이 클 때는 공학 변형률과 차이가 나는 원인이 된다.
전단 변형률 (Shear Strain)\[\gamma_{xy}=\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial X}={D\over T}\]
그린 변형률 성분들은 다음과 같다.
\[\begin{align}E_{xx}&={1\over2}\left(\frac{\partial v}{\partial X}\right)^2={1\over2}\left(D\over T\right)^2\\E_{xy}&={1\over2}\frac{\partial v}{\partial X}={1\over2}{D\over T}\\E_{yy}&=E_{zz}=E_{yz}=E_{zx}=0\end{align}\]
따라서 이 전단 변형의 경우 그린 변형률 텐서는
\[{\bf E}=\begin{bmatrix}{1\over2}\left(D\over T\right)^2&{1\over2}{D\over T}&0\\{1\over2}{D\over T}&0&\\0&0&0\end{bmatrix}\]
그리고 전단항은 정확히 원하던 결과이다. \(E_{11}\) 항은 영이 아닌 결과로 처음에는 의외인 것으로 보인다. 하지만 사실 이것은 장점으로 볼 수 있다. 정사각형의 초기 밑변의 길이는 단순히 T 이다. 하지만 전단 상태의 최종 길이는 \((T^2+D^2)^{1/2}\) 이다. 따라서 \(\Delta L/L_o\)는 다음에 해당한다.
\[{\Delta L\over L_o}=\frac{\sqrt{T^2+D^2}-T}{T}=\sqrt{1+\left(D\over T\right)^2}-1=1+{1\over2}\left(D\over T\right)^2-{1\over8}\left(D\over T\right)^4+\cdots-1\]
여기서 마지막 식은 앞의 식의 테일러 급수 전개(Taylor series expansion) 이다. \(E_{11}\) 항은 실제로 전단에 의한 수평 방향 늘음의 2차식 효과인 것이 명백하다.
다른 유도법 (An Alternative Derivation)
변형구배 F는 다음과 같이 정의된다.
\[{\bf F}=\frac{\partial{\bf x}}{\partial{\bf X}}\]
이것은 다음과 같이 초기 변형전 길이 증분, dX를 변형 후 결과 dx와 연결시키는데 사용될 수 있다.
\[{\bf dx}=\frac{\partial{\bf x}}{\partial{\bf X}}\cdot{\bf dX}={\bf F}\cdot{\bf dX}\]
위의 관계식은 그린 변형률 텐서를 유도하는데 이용할 수 있다.
\[{\bf dx}\cdot{\bf dx}={\bf F}\cdot{\bf dX}\cdot{\bf F}\cdot{\bf dX}={\bf dX}\cdot\left({\bf F}^T\cdot{\bf F}\right)\cdot{\bf dX}\]
위의 결과가 어떻게 조작되었는지 알기 위해서는 아래 텐서 표기법을 참조한다.
\[dx_idx_i=F_{ij}dX_jF_{ik}dX_k=dX_jF_{ij}F_{ik}dX_k=dX_jF_{ji}^TF_{ik}dX_k\]
이에 양변에서 dX·dX를 차감한다.
\[\begin{align}{\bf dx}\cdot{\bf dx}-{\bf dX}\cdot{\bf dX}&={\bf dX}\cdot\left({\bf F}^T\cdot{\bf F}\right)\cdot{\bf dX}-{\bf dX}\cdot{\bf dX}\\&={\bf dX}\cdot\left({\bf F}^T\cdot{\bf F}\right)\cdot{\bf dX}-{\bf dX}\cdot{\bf I}\cdot{\bf dX}\\&={\bf dX}\cdot\left({\bf F}^T\cdot{\bf F}-{\bf I}\right)\cdot{\bf dX}\\&={\bf dX}\cdot2{\bf E}\cdot{\bf dX}\end{align}\]
위의 식은 다음식을 정당화하는데 이용된다.
\[E=\frac{ds^2-dS^2}{2dS^2}=\frac{\left(L_o+\Delta L\right)^2-L_o^2}{2L_o^2}={\Delta L\over L_o}+{1\over2}\left(\Delta L\over L_o\right)^2\]
여기서 ds는 변형 후 길이, dS는 변형 전 길이다. dS에 \(L_o\)를, ds에 \(L_o+\Delta L\)을 대입하면 앞의 결과와 같은 식이 유도된다.
타이어 벨트 예제 (Belt Edge Example)
원통좌표계(cylindrical coordinates) 축대칭(axisymmetric) 원심력을 받는 고속 타이어의 벨트의 단말부(belt edge) 변형률을 계산하는 것이다. 요점은 다음과 같다.
● F가 구해지면 나머지 과정은 직교좌표계와 같이 \({\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F}-{\bf I}\right)\)에 따라 변형률을 구한다.
\[\begin{align}u_r&=0.05R\\u_\theta&=-0.2(R-R_o)\end{align}\]
\(R=R_o\)에서 변형구배를 계산하면 다음을 얻는다.
\[{\bf F}={\bf I}+\nabla{\bf u}=\begin{bmatrix}1+\frac{\partial u_r}{\partial R}&\frac{\partial u_r}{R\partial\theta}-\frac{u_\theta}{R}&\frac{\partial u_r}{\partial Z}\\\frac{\partial u_\theta}{\partial R}&1+\frac{\partial u_\theta}{R\partial\theta}+\frac{u_r}{R}&\frac{\partial u_\theta}{\partial Z}\\\frac{\partial u_z}{\partial R}&\frac{\partial u_z}{R\partial\theta}&1+\frac{\partial u_z}{\partial Z}\end{bmatrix}=\begin{bmatrix}1.05&0&0\\-0.20&1.05&0\\0&0&1\end{bmatrix}\]
그러면 그린 변형률은
\[{\bf E}={1\over2}\left({\bf F}^T\cdot{\bf F}-{\bf I}\right)=\begin{bmatrix}E_{RR}&E_{R\theta}&E_{RZ}\\E_{R\theta}&E_{\theta\theta}&E_{\theta Z}\\E_{RZ}&E_{\theta Z}&E_{ZZ}\end{bmatrix}=\begin{bmatrix}0.071&-0.105&0\\-0.105&0.051&0\\0&0&0\end{bmatrix}\]
위의 예제와 같이 원통좌표계는 종종 직관적이지 않다. 이 경우는 변위가 θ의 함수가 아니지만 원주변형률(circumferential strain) \(E_{\theta\theta}\)가 존재한다. 이 원주변형률은 F의 \(F_{\theta\theta}\) 성분 \(u_r/R\) 항으로부터 나온다. 이 \(u_r/R\) 항은 변형된 원주길이 \(2\pi R_{\rm deformed}\)는 초기 원주길이 \(2\pi R_o\)와 다름을 의미한다.
그러나 위의 고찰보다 여기에는 보다 중요한 사실이 있다. 그것은 F의 편미분을 구하기만 하면 원통좌표계 문제는 없어진다는 것이다. 이 시점 이후로는 이에 대한 처리, 해석 등이 직교좌표계, 또는 그 어떤 시스템인 경우와 동일해진다. 이것은 변형률은 어떻게 구했건 동일한 하나의 변형률이기 때문이다.(응력의 경우도 동일하다.) 모든 변환(transformation), 고유치(principal values), 정수압과 편향 성분(hydrostatics and deviatoric components) 등은 직교좌표계와 같이 원통좌표계에서도 동일하게 적용된다.





댓글
댓글 쓰기