Statically indeterminate three bar by flexibility method

This problem is a statically indeterminated truss system (Figure 1). Let us find the unknown forces of each bar by a flexibility method.

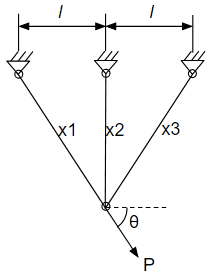Figure 1

\[x_1,\,x_2,\,x_3\ :\ \text{area of each bar, E : young's modulus}\]

We cannot determine each reaction forces by static equilibrium due to lack of the number of equations. So remove the centered bar to apply the flexibility method. Then, we can get the displacement, δ (Figure 2).

Figure 2

\[{\rm F'_1=P,\,F'_3=0,}\,\delta=\frac{{\rm P}l}{{\rm E}x_1\cos\theta}\]

Secondly, the redundant force, \(\rm F_2\) loads the bar upward, and find the displacement, \(u_{\rm F}\) and \(v_{\rm F}\) in the horizontal and vertical direction respectively (Figure 3). We assumed \(x_1<x_3\),

Figure 3

In this case, each reaction force of bar 1 and 3, F' can be found from the equilibrium as below (Figure 4).

Figure 4

\[{\rm F}'={{\rm F}_2\csc\theta\over2}\]

The displacement diagram can be drawn from geometry as Figure 5. Then, we can calculate the displacement in each direction by trigonometry.

Figure 5

\[\delta'_1=\frac{{\rm F}'l_1}{{\rm E}x_1}=\frac{{\rm F}_2l\csc\theta\sec\theta}{2{\rm E}x_1},\ \delta'_3=\frac{{\rm F}'l_3}{{\rm E}x_3}=\frac{{\rm F}_2l\csc\theta\sec\theta}{2{\rm E}x_3}\]

\[u_{\rm F}=\left({\delta'_1-\delta'_3\over2}\right)\sec\theta=\frac{{\rm F}_2l\csc\theta\sec^2\theta}{4{\rm E}}\left({1\over x_1}-{1\over x_3}\right)\]

\[v_{\rm F}=\left({\delta'_1+\delta'_3\over2}\right)\csc\theta=\frac{{\rm F}_2l\csc^2\theta\sec\theta}{4{\rm E}}\left({1\over x_1}+{1\over x_3}\right)\]

Finally, getting back to the original problem, we get to know \({\rm F}_1\) and \({\rm F}_2\) are tensile and \({\rm F}_3\) is compression forces, repectively (Figure 6).

Figure 6

Now, the total downward displacement, \(\delta_2\) by load P is \(\delta\sin\theta-v_{\rm F}\). From the equation, we obtain \({\rm F}_2\). The displacement diagram as shown in Figure 7.

Figure 7

\[\delta\sin\theta=\delta_2+v_{\rm F},\ \frac{{\rm P}l\tan\theta}{{\rm E}x_1}=\frac{{\rm F}_2l\tan\theta}{{\rm E}x_2}+\frac{{\rm F}_2l\csc^2\theta\sec\theta}{4{\rm E}}\left({1\over x_1}+{1\over x_3}\right)\]

\[{\rm F}_2=\frac{4x_2x_3}{4x_1x_3+(x_2x_3+x_1x_2)\csc^3\theta}\]

The other forces \({\rm F}_1\) and \({\rm F}_3\) can be determined from the force equilibrium in horizontal and vertical directions.

\[\rm F_1+F_3=P,\ F_1+F_2\sec\theta-F_3=P\]

\[{\rm F}_1=\frac{4x_1x_3+x_2x_3(\csc^3\theta-2\sec\theta)+x_1x_2\csc^3\theta}{4x_1x_3+(x_2x_3+x_1x_2)\csc^3\theta}{\rm P},\ {\rm F}_3=\frac{2x_2x_3\sec\theta}{4x_1x_3+(x_2x_3+x_1x_2)\csc^3\theta}\]

Now, the stresses and strains in each bar can be found as the equations below.

\[\sigma={{\rm F}\over x},\ \epsilon={\sigma\over{\rm E}}\]