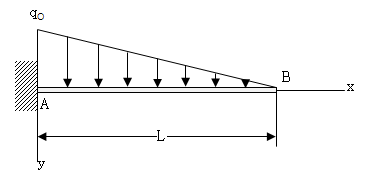
처짐곡선 방정식에 의한 부정정보 해석 (Statically Indeterminate Beam by Deflection Curve Equations)
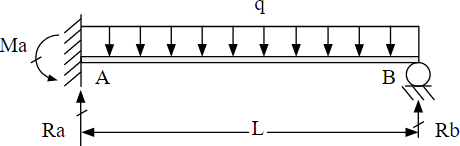
부정정보(statically indeterminate beam) 는 처짐곡선의 미분방정식 중 하나를 풀어 해석할 수 있다. 그 과정은 정정보(determinate beam)과 근본적으로 같으며( 굽힘모멘트 적분 / 전단력과 하중 적분 / 면적모멘트법에 의한 보의 처짐 참조), 미분방정식을 쓰고, 일반해를 얻기 위해 적분하며, 그 다음 적분상수를 구하기 위해 경계조건을 적용한다. [예제 1] 균일분포하중 q를 받고 있는 일단고정 타단지지 보(propped cantilever beam) AB가 아래 그림에 나타나 있다. 반력 Ra, Rb 및 Ma를 결정하여라. 예제 1. 일단고정 타단지지 보 Rb를 미지수로 선택한다. 그 다음 평형방정식으로부터 A에서의 반력을 Rb의 항으로 얻을 수 있다. \[R_a=qL-R_b\qquad M_a={qL^2\over2}-R_bL\qquad\cdots(1)\] 이제 Rb의 항으로 아래 자유물체도(free body diagram)로부터 굽힘모멘트 의 알반 표현식을 얻을 수 있다. \[M=R_ax-M_a-{qx^2\over2}=qLx-R_bx-{qL^2\over2}+R_bL-{qx^2\over2}\] 처짐곡선의 2차 미분방정식은 \[EIv''=-M=-qLx+R_bx+{qL^2\over2}-R_bL+{qx^2\over2}\] 그리고 두번 연속 적분하면 다음식을 얻는다. \[\begin{split}&EIv'=-{qLx^2\over2}+{R_bx^2\over2}+{qL^2x\over2}-R_bLx+{qx^3\over6}+C_1\\&EIv=-{qLx^3\over6}+{R_bx^3\over6}+{qL^2x^2\over4}-{R_bLx^2\over2}+{qx^4\over24}+C_1x+C_2\end{split}\] 윗식들에는 세개의 미지수(C1, C2 및 Rb)와 다음 세개의 경계조건이 있다: \[v(0)=v'(0)=v(L)=0\] 이들 조건을 앞의 식에 대입하면 C1=C2=0, 그리고 \[...