전단력과 하중 적분에 의한 보의 처짐 (Deflections by Shear Force and Load Integration)
전단력 V와 분포하중 q의 항으로 나타낸 처짐곡선의 방정식으로도 보의 처짐을 구할 수 있다. 그 과정은 보다 많은 적분이 요구되는 것 외에는 굽힘모멘트 방정식과 유사하다. 예를 들면 4차 하중 방정식으로 출발하면 처짐 방정식을 구하기 위해서는 4번의 적분이 필요하다. 따라서 추가적인 적분 상수가 도출되나 경계 및 연속조건(boundary and continuity conditions)으로 이들 상수를 구할 수 있다. 이제 이 조건들은 기울기와 처짐뿐만 아니라 전단력과 굽힘모멘트에 대한 것도 포함된다.
예제 1
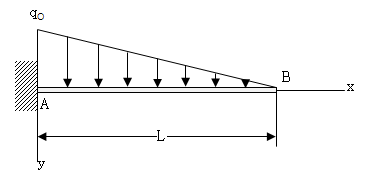
최대강도 \(q_o\)인 삼각형 분포하중을 지지하는 외팔보 AB의 처짐곡선 방정식을 결정하라(아래 그림). 또한 자유단의 처짐 \(\delta_b\)와 회전각 \(\theta_b\)를 결정하라.
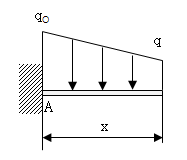
분포하중의 강도는 다음 식으로 주어진다.
\[q={q_o(L-x)\over L}\]
따라서 4차 미분방정식은 다음과 같다.
\[EIv^{(4)}=q={q_o(L-x)\over L}\]
1차 적분을 하면
\[EIv'''=-V=-{q_o(L-x)^2\over2L}+C_1\]
x=L에서 전단력은 0 이므로 v'''(L)=0 이다. 이 조건으로부터 \(C_1=0\)을 얻는다.
2차 적분을 통해서 다음식을 얻는다.
\[EIv''=-M={q_o(L-x)^3\over6L}+C_2\]
이 식은 굽힘모멘트 방정식이다. 두번째 경계조건으로 자유단에서 굽힘모멘트는 0 이다: v''(L)=0. 이 조건으로부터 \(C_2=0\)을 얻는다.
3차와 4차 적분을 수행하면
\[\begin{align}&EIv'=-{q_0\over24L}(L-x)^4+C_3\\&EIv={q_o\over120L}(L-x)^5+C_3x+C_4\end{align}\]
고정단의 경계조건 v'(0)=v(0)=0 으로부터
\[C_3={q_oL^3\over24}\qquad C_4={q_oL^4\over120}\]
이 표현식들을 원래 방정식에 대입하면 보의 기울기와 처짐에 대한 다음 방정식을 얻는다.
\[\begin{align}&v'={q_ox\over24LEI}(4L^3-6L^2x+4Lx^2-x^3)\\&v={q_ox^2\over120LEI}(10L^3-10L^2+5Lx^2-x^3)\end{align}\]
자유단(x=L)에서의 회전각 \(\theta_b\)와 처짐 \(\delta_b\)는 이제 이 식들로부터 쉽게 얻어진다.
\[\theta_b={q_oL^3\over24EI}\qquad\delta_b={q_oL^4\over30EI}\]
예제 2
집중하중 P를 받고 돌출부(overhang)를 가진 단순보(simple beam)의 처짐곡선 방정식을 결정하라(아래 그림). 지지부 간 폭은 L 이고 돌출부는 L/2 이다.
지지부 A와 B의 반력 때문에 보의 AB와 BC 부분의 미분방정식을 따로 써야 한다. 반력들은 각 지지부의 모멘트 평형으로부터 다음과 같이 구해진다.
\[\sum{M_A}=\sum{M_B}=R_AL+{PL\over2}=R_BL-{3PL\over2}=0\]
위의 자유물체도의 평형으로부터 전단력과 3차 미분방정식은
\[\begin{split}&EIv'''=-V={P\over2}\qquad(0<x<L)\\&EIv'''=-V=-P\qquad\left(L<x<{3L\over2}\right)\end{split}\]
이 방정식들을 적분하면 다음과 같은 굽힘모멘트 방정식이 나온다:
\[\begin{split}&EIv''=M={Px\over2}+C_1\qquad(0\le x\le L)\\&EIv''=M=-Px+C_2\qquad\left(L\le x\le{3L\over2}\right)\end{split}\]
A와 B점의 굽힘모멘트는 0 이다; 따라서 경계조건 v''(0)=v''(3L/2)=0을 가진다. 이들 조건으로부터 \(C_1=0,\,C_2=3PL/2\)를 얻는다.
다음 적분을 하면
\[\begin{align}&EIv'={Px^2\over4}+C_3\qquad(0\le x\le L)\\&EIv'={Px(3L-x)\over2}+C_4\qquad\left(L\le x\le{3L\over2}\right)\end{align}\]
기울기의 유일한 경계조건은 지지점 B의 연속조건이다: AB 구간 v'(L)=BC 구간 v'(L), 즉
\[{PL^2\over4}+C_3=PL^2+C_4\qquad C_4=C_3-{3PL^2\over4}\]
마지막 적분을 하면 다음식을 준다.
\[\begin{align}&EIv={Px^3\over12}+C_3x+C_5\qquad(0\le x\le L)\\&EIv={Px^2(9L-2x)\over12}+C_4x+C_6\qquad\left(L\le x\le {3L\over2}\right)\end{align}\]
A와 B점에서의 처짐은 0 이므로 3개의 경계조건을 더 얻는다: v(0)=AB 구간 v(L)=BC 구간 v(L)=0. 그 결과 상수들에 대한 방정식은
\[C_5=0\qquad C_3={PL^3\over12}\qquad C_4L+C_6=-{7PL^3\over12}\]
위의 결과들을 조합하면
\[C_4=-{5PL^2\over6}\qquad C_6={PL^3\over4}\]
따라서 보의 처짐곡선 방정식은
\[\begin{align}&v=-{Px\over12EI}(L^2-x^2)\qquad(0\le x\le L)\\&v={P\over12EI}(3L-x)(L-x)(L-2x)\qquad\left(L\le x\le{3L\over2}\right)\end{align}\]
위의 식으로부터 돌출부 끝단의 처짐을 구한다(x=3L/2).
\[\delta_c={PL^3\over8EI}\]
B와 C 사이의 보의 처짐은 아래 방향이고 A와 B 사이는 윗 방향임에 유의한다.





댓글
댓글 쓰기