삼각함수 항등식 (Trigonometric Identity)

피타고라스 정리

\(\sin^2\theta+\cos^2\theta=1\)

\(\tan^2\theta+1=\sec^2\theta\)

\(\cot^2\theta+1=\csc^2\theta\)

<증명>

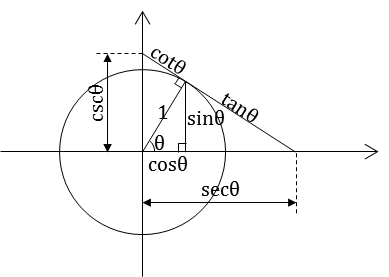
반경이 1 인 단위원을 그려서 파타고라스의 정리를 적용한다.

덧셈정리

\(\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\)

\(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)

\(\tan(\alpha\pm\beta)=\dfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\)

<증명>

한 각이 β 인 직각삼각형을 각도 α로 직사각형에 내접시킨다. 각 변의 길이를 삼각함수로 나타내고 직사각형의 대변의 길이는 같으므로 등식이 증명된다. (sin/cos은 직각삼각형의 빗변의 길이가 '1', tan는 직사각형 밑변의 길이 '1'을 적용한다.)

2배각의 공식

\(\sin2\theta=2\sin\theta\cos\theta\)

\(\cos2\theta=\cos^2\theta-\sin^2\theta=2\cos^2\theta-1=1-2\sin^2\theta=\dfrac{1-\tan^2\theta}{1+\tan^2\theta}\)

\(\tan2\theta=\dfrac{2\tan\theta}{1-\tan^2\theta}\)

<증명>

\(\sin2\theta=\sin(\theta+\theta)=\sin\theta\cos\theta+\cos\theta\sin\theta=2\sin\theta\cos\theta\)

\(\begin{align*}\cos2\theta&=\cos(\theta+\theta)=\cos\theta\cos\theta-\sin\theta\sin\theta=\cos^2\theta-\sin^2\theta=\cos^2\theta-(1-\cos^2\theta)\\&=2\cos^2\theta-1=(1-\sin^2\theta)-\sin^2\theta=1-2\sin^2\theta\\&=\frac{\cos^2\theta-\sin^2\theta}{\cos^2\theta+\sin^2\theta}=\frac{1-\frac{\sin^2\theta}{\cos^2\theta}}{1+\frac{\sin^2\theta}{\cos^2\theta}}=\frac{1-\tan^2\theta}{1+\tan^2\theta}\end{align*}\)

\(\tan2\theta=\dfrac{\tan\theta+\tan\theta}{1-\tan\theta\tan\theta}=\dfrac{2\tan\theta}{1-\tan^2\theta}\)

3배각의 공식

\(\sin3\theta=-4\sin^3\theta+3\sin\theta\)

\(\cos3\theta=\ \ 4\cos^3\theta-3\cos\theta\)

<증명>

\(\begin{split}\sin3\theta&=\sin(\theta+2\theta)=\sin\theta\cos2\theta+\cos\theta\sin2\theta=\sin\theta(1-2\sin^2\theta)+2(1-\sin^2\theta)\sin\theta\\&=-4\sin^3\theta+3\sin\theta\end{split}\)

\(\begin{split}\cos3\theta&=\cos(\theta+2\theta)=\cos\theta\cos2\theta-\sin\theta\sin2\theta=\cos\theta(2\cos^2\theta-1)-2(1-\cos^2\theta)\cos\theta\\&=\ \ 4\cos^3\theta-3\cos\theta\end{split}\)

곱을 합으로 바꾸는 공식

\(\sin x\sin y=\dfrac{\cos(x-y)-\cos(x+y)}{2}\)

\(\sin x\cos y=\dfrac{\sin(x+y)+\sin(x-y)}{2}\)

\(\cos x\sin y=\dfrac{\sin(x+y)-\sin(x-y)}{2}\)

\(\cos x\cos y=\dfrac{\cos(x-y)+\cos(x+y)}{2}\)

<증명>

우변을 덧셈정리로 전개한다.