기계공학 (Mechanical Engineering)

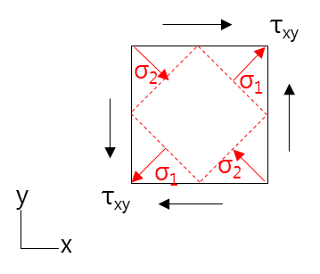
주응력과 응력 불변량 은 응력 의 정의와 상관없이 적용 가능하다. 2등급(2nd rank) 텐서의 좌표변환은 어떠한 응력, 변형률 에도 적용할 수 있으며 다음과 같이 나타낸다. \(\boldsymbol\sigma'={\bf Q}\ \boldsymbol\sigma\ {\bf Q}^T\) 다음의 내용들은 대칭 텐서이며 위의 좌표변환 이 사용된다는 전제로 한다. 2-D 주응력 (2-D Principal Stress) 2-D 변환 방정식은 다음과 같다. \(\begin{split}\sigma'_{xx}&=\sigma_{xx}\cos^2\theta+\sigma_{yy}\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta\\\sigma'_{yy}&=\sigma_{xx}\sin^2\theta+\sigma_{yy}\cos^2\theta-2\tau_{xy}\sin\theta\cos\theta\\\tau'_{xy}&=\left(\sigma_{yy}-\sigma_{xx}\right)\sin\theta\cos\theta+\tau_{xy}\left(\cos^2\theta-\sin^2\theta\right)\end{split}\) 아래 그림의 좌표축과 평행한 정사각형은 순수전단(pure shear) 상태이다. 그러나 적색 내접 사각형은 단순 인장/압축을 받고 있다. 이 응력들이 전역 좌표계(global coordinates)에서 순수전단의 주응력(principal value)이다. 주방향에서는 전단응력이 '0' 이므로 주응력 각도 \(\theta_p\)는 \(\tau'_{xy}=0\)으로 하면 구할 수 있다. \(0=\left(\sigma_{yy}-\sigma_{xx}\right)\sin\theta_p\cos\theta_p+\tau_{xy}\left(\cos^2\theta_p-\sin^2\theta_p\right)\) 삼각함수 항등식 을 활용하여 정리하면 \(\tan2\theta_

[문  제] \(\displaystyle\lim_{x\to a}x^2=a^2\) 임을 ε-δ 법 에 의하여 증명하여라. <증  명> 임의의 ε>0가 주어지고 \(\lvert f(x)-a^2\rvert<\epsilon\) 이기 위해서는 \(\lvert x^2-a^2\rvert=\lvert x-a\rvert\lvert x+a\rvert<\epsilon\). 즉, \(\lvert x-a\rvert<\frac{\epsilon}{\lvert x+a\rvert}\) 이면 된다. \(0<\lvert x-a\rvert<\delta\) 에서 δ=1 로 놓으면 \(\lvert x\rvert-\lvert a\rvert\le\lvert x-a\rvert<1\) 이므로 \(\lvert x\rvert<\lvert a\rvert+1\). 따라서 \(\lvert x+a\rvert\le\lvert x\rvert+\lvert a\rvert<1+2\lvert a\rvert\) 이다. 곧, \(\frac{\epsilon}{1+2\lvert a\rvert}<\frac{\epsilon}{\lvert x+a\rvert}\) 이다. 위의 사실로부터 \(\delta=\min\left(1,\frac{\epsilon}{1+2\lvert a\rvert}\right)\) 이고 \(0<\lvert x-a\rvert<\delta\) 인 x에 대하여 \(\lvert f(x)-a^2\rvert<\epsilon\). \[\therefore\lim_{x\to a}x^2=a^2\]

개요 (Introduction) 기둥의 좌굴은 특별하고 독특한 주제이다. 이는 붕괴(failure)가 재료 강도와 무관한 유일한 구조역학 분야이다. 기둥 좌굴해석(column buckling analysis) 은 기둥이 좌굴 전에 지지할 수 있는 최대하중을 결정하는 것이다. 하지만 장주(長柱, long column)의 경우, 좌굴은 재료 강도와 관계가 없다. 대신에 기둥의 재료 및 치수에 의한 강성이 지배적이다. 본 글에서는 두 가지 접근법으로 기둥 좌굴의 표준 방정식을 유도한다. 먼저 방정식의 일반적 유도법, 즉 오일러 좌굴이론(Euler Buckling Theory) 을 다룬다. 이는 공학 과정의 교과서에 실린 유도법이지만 좌굴 과정을 지배하는 물리적 기구를 만족스럽게 설명하지 못한다. 이것이 좌굴 방정식의 두번째 유도법이 제시된 이유이다. 특이하게도, 여기서와 같이 물체가 축방향으로 압축 하중을 받으면 기둥 이라 부르지만, 횡방향으로 하중을 받으면 보(beam) 라고 불리운다. 그럼에도 불구하고, 보 굽힘이론은 기둥 좌굴해석의 핵심이므로, 보의 굽힘 글을 사전에 복습할 것을 추천한다. 오일러 좌굴이론 (Euler Buckling Theory) 오일러 좌굴이론은 강의 교재에서 다루는 고전 이론이다. 이는 P의 압축하중으로 y 만큼 처진 기둥의 내부 굽힘모멘트(internal bending moment)는 -Py이다는 것에서 출발한다. 따라서 -Py를 보의 굽힘방정식 M에 대입한다. \(EIy''=M=-Py\) 위의 식으로부터 다음 미분 방정식을 얻는다. \(EIy''+Py=0\) 이 방정식의 일반해는 다음과 같다. \(y=A\sin\left(\sqrt{P\over{EI}}x\right)+B\cos\left(\sqrt{P\over{EI}}x\right)\) 여기서 A와 B는 경계조건으로부터 결정되는 상수이다. 경계조건은 x=0 및 x=L 에서 y=0 이다. 첫번째 경계조건으로부터 B=0 이고, 두번째 경계조건을 적용하면 다