주응력 (Principal Stress)

주응력과 응력 불변량은 응력의 정의와 상관없이 적용 가능하다.

2등급(2nd rank) 텐서의 좌표변환은 어떠한 응력, 변형률에도 적용할 수 있으며 다음과 같이 나타낸다.

\(\boldsymbol\sigma'={\bf Q}\ \boldsymbol\sigma\ {\bf Q}^T\)

다음의 내용들은 대칭 텐서이며 위의 좌표변환이 사용된다는 전제로 한다.

2-D 주응력 (2-D Principal Stress)

2-D 변환 방정식은 다음과 같다.

\(\begin{split}\sigma'_{xx}&=\sigma_{xx}\cos^2\theta+\sigma_{yy}\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta\\\sigma'_{yy}&=\sigma_{xx}\sin^2\theta+\sigma_{yy}\cos^2\theta-2\tau_{xy}\sin\theta\cos\theta\\\tau'_{xy}&=\left(\sigma_{yy}-\sigma_{xx}\right)\sin\theta\cos\theta+\tau_{xy}\left(\cos^2\theta-\sin^2\theta\right)\end{split}\)

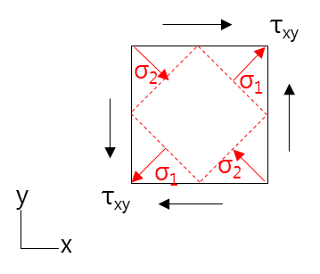
아래 그림의 좌표축과 평행한 정사각형은 순수전단(pure shear) 상태이다. 그러나 적색 내접 사각형은 단순 인장/압축을 받고 있다. 이 응력들이 전역 좌표계(global coordinates)에서 순수전단의 주응력(principal value)이다.

주방향에서는 전단응력이 '0' 이므로 주응력 각도 \(\theta_p\)는 \(\tau'_{xy}=0\)으로 하면 구할 수 있다.

\(0=\left(\sigma_{yy}-\sigma_{xx}\right)\sin\theta_p\cos\theta_p+\tau_{xy}\left(\cos^2\theta_p-\sin^2\theta_p\right)\)

삼각함수 항등식을 활용하여 정리하면

\(\tan2\theta_p=\dfrac{2\tau_{xy}}{\sigma_{xx}-\sigma_{yy}}\)

이 때 변환행렬 Q는

\({\bf Q}=\left[\begin{matrix}\cos\theta_p&\sin\theta_p\\-\sin\theta_p&\cos\theta_p\end{matrix}\right]\)

주응력 \(\sigma_{1,2}\) 역시 삼각함수 항등식을 활용한다. 먼저 \(2\theta_p\)를 내각으로 하는 직각삼각형의 세변은 다음과 같다.

\(R=\sqrt{\left(\dfrac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau^2}\)

또한 \(\cos^2\theta=(1+\cos2\theta)/2\), \(\sin^2\theta=(1-\cos2\theta)/2\) 및 \(2\sin\theta\cos\theta=\sin2\theta\) 이므로 \(\sigma'_{xx}\) 변환 방정식에서

\(\begin{split}\sigma_1&=\sigma_{xx}\left(\frac{1+\cos2\theta_p}{2}\right)+\sigma_{yy}\left(\frac{1-\cos2\theta_p}{2}\right)+\tau_{xy}\sin2\theta_p\\&=\frac{\sigma_{xx}+\sigma_{yy}}{2}+\frac{\sigma_{xx}-\sigma_{yy}}{2}\left(\frac{\sigma_{xx}-\sigma_{yy}}{2R}\right)+\tau_{xy}\left(\frac{\tau_{xy}}{R}\right)\\&=\frac{\sigma_{xx}+\sigma_{yy}}{2}+\sqrt{\left(\frac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau_{xy}^2}\end{split}\)

\(\sigma_2(<\sigma_1)\)은 \(\sigma_1+\sigma_2=\sigma_{xx}+\sigma_{yy}\) 이므로 주응력 \(\sigma_{1,2}\)는 아래와 같이 쓸 수 있다.

\(\sigma_{1,2}=\dfrac{\sigma_{xx}+\sigma_{yy}}{2}\pm\sqrt{\left(\dfrac{\sigma_{xx}-\sigma_{yy}}{2}\right)^2+\tau_{xy}^2}\)

[예  제] 응력 텐서가 다음과 같을 때 주방향과 주응력을 구하라.

\(\boldsymbol\sigma=\left[\begin{matrix}50&30\\30&-20\end{matrix}\right]\)

\(\begin{split}&\theta_p={1\over2}{\rm Tan}^{-1}\left(\frac{2\cdot30}{50-(-20)}\right)=20.3^\circ\\&\sigma_{1,2}=\frac{50-20}{2}\pm\sqrt{\left(\frac{50+20}{2}\right)^2+30^2}=61.1,\ -31.1\end{split}\)

위의 방정식을 이용하면 어느 주응력이 20.3˚ 이고 어느 것이 110.3˚(20.3˚+90˚) 인지 모른다는 제약이 따른다. 그러므로 다음과 같이 변환행렬을 이용하는 것이 유용하다.

\(\begin{split}\begin{bmatrix}\sigma_1&0\\0&\sigma_2\end{bmatrix}&=\begin{bmatrix}\cos20.3^\circ&\sin20.3^\circ\\-\sin20.3^\circ&\cos20.3^\circ\end{bmatrix}\begin{bmatrix}50&30\\30&-20\end{bmatrix}\begin{bmatrix}\cos20.3^\circ&-\sin20.3^\circ\\\sin20.3^\circ&\cos20.3^\circ\end{bmatrix}\\&=\begin{bmatrix}61.1&0.0\\0.0&-31.1\end{bmatrix}\end{split}\)

위의 결과는 \(\sigma_1\) 텐서항의 61.1 이 x축으로부터 20.3˚ 이고  \(\sigma_2\)는 그것으로부터 90˚ 방향임을 보여준다.

3-D 주응력 (3-D Principal Stress)

3-D 응력 좌표변환은 다음과 같다.

\(\begin{bmatrix}\sigma'_{11}&\sigma'_{12}&\sigma'_{13}\\\sigma'_{21}&\sigma'_{22}&\sigma'_{23}\\\sigma'_{31}&\sigma'_{32}&\sigma'_{33}\end{bmatrix}=\begin{bmatrix}Q_{11}&Q_{12}&Q_{13}\\Q_{21}&Q_{22}&Q_{23}\\Q_{31}&Q_{32}&Q_{33}\end{bmatrix}\begin{bmatrix}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}\end{bmatrix}\begin{bmatrix}Q_{11}&Q_{21}&Q_{31}\\Q_{12}&Q_{22}&Q_{32}\\Q_{13}&Q_{23}&Q_{33}\end{bmatrix}\)

최대 전단응력 (Maximum Shear Stress) 임의의 점의 최대 전단응력은 주응력으로부터 쉽게 구할 수 있다. \(\tau_{\rm max}=\dfrac{\sigma_1-\sigma_3}{2}\) 여기서 \(\sigma_1\ge\sigma_2\ge\sigma_3\) 이다. 위의 식은 2-D, 3-D 상관없이 적용할 수 있다. 최대 전단응력은 항상 주방향의 45˚ 회전면에서 발생한다. 만약 주응력 텐서가 아래와 같으면 \(\boldsymbol\sigma=\begin{bmatrix}24&0&0\\0&125&0\\0&0&433\end{bmatrix}\) 최대/최소 주응력은 각각 \(\sigma_{33},\,\sigma_{11}\) 위치에 있으므로 최대 전단응력 방향은 주방향 (1-3)면 방향으로 45˚ 회전함으로 구해진다. 최대 전단응력 값은 \(\tau_{\rm max}=\dfrac{433-24}{2}=205\)

주응력을 구하기 위해서는 응력 텐서의 고유치에 대한 3차 방정식을 풀어야 한다. 이 방정식은 다음 행렬식을 '0'으로 하여 유도된다.

\(\begin{vmatrix}\sigma_{11}-\lambda&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}-\lambda&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}-\lambda\end{vmatrix}=0\)

이 행렬식을 풀면

\(\lambda^3-(\sigma_{11}+\sigma_{22}+\sigma_{33})\lambda^2+(\sigma_{11}\sigma_{22}+\sigma_{22}\sigma_{33}+\sigma_{33}\sigma_{11}-\sigma_{12}^2-\sigma_{23}^2-\sigma_{31}^2)\lambda-(\sigma_{11}\sigma_{22}\sigma_{33}-\sigma_{11}\sigma_{23}^2-\sigma_{22}\sigma_{31}^2-\sigma_{33}\sigma_{12}^2+2\sigma_{12}\sigma_{23}\sigma_{31})=0\)

여기서 주응력은 응력 텐서의 어떠한 좌표변환을 하여도 같은 값을 가져야 하므로 위의 방정식의 계수는 불변량이러야 한다. 따라서 이들을 응력 불변치(stress invariants)라 부르고 다음과 같이 나타낸다.

\(\rm\lambda^3-I_1\lambda^2+I_2\lambda-I_3=0\)

여기서

\(\begin{split}&\rm I_1=tr(\boldsymbol\sigma)=\sigma_{11}+\sigma_{22}+\sigma_{33}\\&\rm I_2=\begin{vmatrix}\sigma_{11}&\sigma_{12}\\\sigma_{21}&\sigma_{22}\end{vmatrix}+\begin{vmatrix}\sigma_{22}&\sigma_{23}\\\sigma_{32}&\sigma_{33}\end{vmatrix}+\begin{vmatrix}\sigma_{11}&\sigma_{13}\\\sigma_{31}&\sigma_{33}\end{vmatrix}=\sigma_{11}\sigma_{22}+\sigma_{22}\sigma_{33}+\sigma_{33}\sigma_{11}-\sigma_{12}^2+\sigma_{23}^2-\sigma_{31}^2\\&\rm I_3=\det(\boldsymbol\sigma)=\sigma_{11}\sigma_{22}\sigma_{33}-\sigma_{11}\sigma_{23}^2-\sigma_{22}\sigma_{31}^2-\sigma_{33}\sigma_{12}^2+2\sigma_{12}\sigma_{23}\sigma_{31}\end{split}\)

텐서 표기법으로 쓰면

\(\rm I_1=\sigma_{kk},\quad I_2=\dfrac{1}{2}\left(\sigma_{kk}^2-\sigma_{ij}\sigma_{ij}\right),\quad I_3=\epsilon_{ijk}\sigma_{i1}\sigma_{j2}\sigma_{k3}\)

불변치의 물리적 해석 (Physical Interpretation of Invariants) 불변치의 물리적 의미는 어떤 텐서에서 계산되었는지에 따라 다르다. 응력과 변형률의 경우 \(\rm I_1\)은 정수압 성분(hydrostatic componet)을 나타낸다. \(\rm I_2\)는 응력과 변형률의 편향(deviatoric) 성분과 관련이 있는 경향이 있다. \(\rm I_3\)는 응력과 변형률의 행렬식으로 물리적 의미는 없어 보인다. 하지만, 변형구배(deformation gradient)에서는 \(\rm I_3=V_f/V_o\) 초기 대비 체적비를 의미하고 고무와 같이 비압축성(incompressible) 재료에서는 '1'이 된다.

[예  제] 응력 텐서가 아래와 같을 때 불변치와 주응력을 구하라.

\({\rm \sigma}=\begin{bmatrix}50&30&20\\30&-20&-10\\20&-10&10\end{bmatrix}\)

응력 불변치는 위의 식에 각 응력 성분을 대입하면 구해진다.

\(\rm I_1=50-20+10=40\)

\(\rm I_2=50(-20)+(-20)10+10\cdot50-30^2-20^2-(-10)^2=-2,100\)

\(\rm I_3=50(-20)10+30(-10)20+20\cdot30(-10)-50(-10)(-10)-30\cdot30\cdot10-20(-20)20=-28,000\)

주응력을 구하기 위한 고유치의 3차 방정식은 다음과 같다.

\(\lambda^3-40\lambda^2-2100\lambda+28000=0\)

3차 방정식의 해는 주응력이며 3차 방정식의 근의 공식을 이용하여 계산한다.

먼저, 매개변수 Q, R, θ를 다음과 같이 구한다.

\(\rm Q=\dfrac{3I_2-I_1^2}{9},\quad R=\dfrac{2I_1^3-9I_1I_2+27I_3}{54},\quad\theta=Cos^{-1}\left(\dfrac{R}{\sqrt{-Q^3}}\right)\)

최종적으로 주응력은 위의 매개변수를 대입하여 아래와 같이 구한다.

\(\begin{split}&\rm\sigma_1=2\sqrt{-Q}\cos\left(\dfrac{\theta}{3}\right)+\dfrac{I_1}{3}=65.5\\&\rm\sigma_2=2\sqrt{-Q}\cos\left(\dfrac{\theta+2\pi}{3}\right)+\dfrac{I_1}{3}=-37.1\\&\rm\sigma_3=2\sqrt{-Q}\cos\left(\dfrac{\theta+4\pi}{3}\right)+\dfrac{I_1}{3}=11.5\end{split}\)

또한, 행렬로 나타내면

\(\boldsymbol\sigma'=\begin{bmatrix}65.5&0&0\\0&-37.1&0\\0&0&11.5\end{bmatrix}\)

출처 : http://www.continuummechanics.org/