통계적 추정

통계적 추정

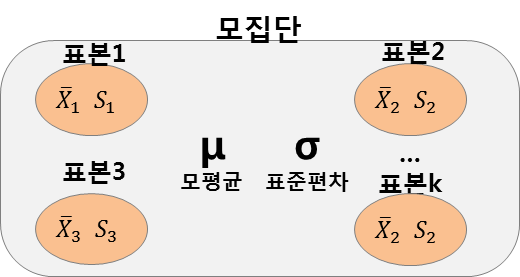
표본의 특성을 나타내는 통계량을 기초로 하여 모집단의 특성인 모수를 추측하는 통계적 분석을 말한다.

점추정	모수를 단일치로 추측한다. 틀릴 가능성이 크며 신뢰도를 확률로 나타낼 수 없다.
구간추정	모수를 포함할 것으로 예측되는 구간을 추측한다. 모수 추정치와 신뢰도를 확률로 구할 수 있다.

점추정

모수의 점추정량은 다음과 같이 표본 통계량의 단일치로 추정한다.

(1) 모평균         ← 표본평균 (\(\overline X\))
(2) 모분산         ← 표본분산 (\(S^2\))
(3) 모표준편차 ← 표본표준편차 (\(S\))

표준오차 (Standard Error)

모평균(\(\mu\))과 개별 표본평균\(\left(\overline{X}_1,\,\overline{X}_2,\,\cdot\cdot\cdot,\overline{X}_k\right)\)의 차이를 추정한 값이다.

표본평균이 모평균을 기준으로 얼마나 흩어져 있는 지를 나타낸다. 즉, 표본평균의 표준편차이다.

중심극한정리에 의해 표준오차는 다음식으로 표현된다.

\(SE=\dfrac{\sigma}{\sqrt{n}}\) 여기서 n은 표본평균에 사용된 데이터의 개수

신뢰수준 (Confidence Level)

구간추정 시 해당 구간 내에 추정하고자 하는 모수가 있을 확률이다. 신뢰수준 95%는 해당 모수를 100번 추정했을 때 신뢰구간 내에 95번 정도 포함된다는 의미이다. 일반적으로 90%, 95%, 99% 를 사용한다.

신뢰구간 (Confidence Interval)

해당 신뢰수준에서 모수가 포함될 구간을 말한다. 신뢰구간이 크면 모수의 추정범위가 커지므로 정보로서의 가치가 떨어진다.

신뢰수준이 정확성과 관련은 있으나 그 자체가 정확성을 나타내는 것은 아니다. 모수를 더 정확하게 추정하려면 신뢰구간의 폭을 줄이는 것이 필요하다.

신뢰구간 추정

모수에 맞는 확률분포와 신뢰수준을 정하면 그에 해당하는 임계치가 정해진다. 확률분포는 평균이 0, 표준편차가 1로 맞추어져 있으므로 표본평균의 점추정량과 표준오차를 사용하여 임계치를 표본의 스케일로 변환해 준다.

경우1 : 모집단의 표준편차를 안다.

경우2 : 모집단의 표준편차를 모르고, 표본의 크기가 크다.

경우3 : 모집단의 표준편차를 모르고, 표본의 크기가 작다.

모평균 \(\mu\)에 대한 \((1-\alpha)\) 신뢰구간

경우1 : \(\overline{X}-Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\ge\mu\ge\overline{X}+Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\)

경우2 : \(\overline{X}-Z_{\alpha/2}\frac{S}{\sqrt{n}}\ge\mu\ge\overline{X}+Z_{\alpha/2}\frac{S}{\sqrt{n}}\)

경우3 : \(\overline{X}-t_{\alpha/2}\frac{S}{\sqrt{n}}\ \ge\mu\ge\overline{X}+\ t_{\alpha/2}\frac{S}{\sqrt{n}}\)

● 신뢰구간의 범위는 신뢰수준과 표준오차에 의해 결정된다.

● 대부분 모집단의 표준편차를 모르므로 모표준편차 \(\sigma\)를 표본표준편차 S로 대체하여 경우2, 경우 3의 식이 사용된다.

[예제] 8 대의 A-엔진에 대한 실측 출력이 아래와 같을 때 전체 A-엔진 출력의 점추정치, 표준오차 및 구간 추정치(신뢰수준 95%)를 구하여라.

실측출력(PS)

114.2

115.4

110.9

110.9

122.1

113.1

115.4

109.8

1) 점추정치 : 8 대 엔진의 출력평균

\(\overline{X}=\frac{114.2+115.4+\cdot\cdot\cdot+109.8}{8}=113.975\)

2) 표준오차 : 모표준편차를 모르므로 표본표준편차를 사용한다.

\(\overline{S}=\sqrt{\frac{(114.2-113.975)^2+(115.4-113.975)^2+\cdot\cdot\cdot+(109..8-113.975)^2}{8-1}}=3.914\)

\(\therefore\ {\rm 표준오차}(SE)=\frac{3.914}{\sqrt{8}}=1.384\)

3) 구간추정치 : 데이터 개수가 8개(<30)이고 평균을 추정하는 것이므로 t-분포를 사용한다. 신뢰수준 95%의 t-분포 임계치는 \(t_{0.05/2}=2.365\) 이다(엑셀함수 tinv(0.05,7)). 위의 결과에 따라 아래 식으로 구간 추정치를 계산한다.

 \(\overline{X}-t_{\alpha/2}\frac{S}{\sqrt{n}}\ge\mu\ge\overline{X}+t_{\alpha/2}\frac{S}{\sqrt{n}}\)

① 하한치 : 113.975 - 2.365 × 1.384 = 110.703

② 상한치 : 113.975 + 2.365 × 1.384 = 117.247

∴ 신뢰구간 : 110.703 ≤ μ ≤ 117.247

표본 크기와 신뢰구간

신뢰구간의 범위 크기를 결정하는 것은 신뢰수준과 표본오차이지만, 일반적으로 신뢰수준은 정해진 값을 사용하므로, 신뢰구간에 실질적으로 영향을 주는 것은 표준오차라고 할 수 있다.

중심극한정리에 의해 표준오차는 \(\sigma/\sqrt{n}\) (모표준편차를 모르는 경우 \(S/\sqrt{n}\))이다. 따라서 표본의 개수가 많을수록 모수에 관한 정보가 확실해 지므로 신뢰구간 크기가 작아지고, 표본이 작을수록 신뢰구간이 커지게 된다. 다시 말하면 신뢰수준을 유지한 상태에서 오차 범위가 줄어들게 신뢰구간을 정하려면 표본의 크기가 커져야 한다.

신뢰구간의 결정