극좌표계 성형한계도 (PEPS FLD)

극좌표계 성형한계도(Polar-coordinated Effective Plastic Strain Forming Limit Diagram)는 EPS, \(\overline{\epsilon_p}\)를 도입하여, 직교좌표계 X-Y 평면에 극좌표계를 이용하여 성형한계를 표시한다. (x, y) 좌표는 \((\overline{\epsilon_p}\sin\theta,\,\overline{\epsilon_p}\cos\theta)\)로 구해지며 이 때의 x, y의 값은 물리적 의미를 갖지 않고, 단지 극좌표계 상의 값을 직교좌표계에 옮기기 위한 값으로 간주된다.

이 때의 \(\overline{\epsilon_p}\)와 θ는 다음과 같이 결정된다.

\(\overline{\epsilon_p}=\frac{1+\overline r}{\sqrt{1+2\overline r}}\int_0^t\sqrt{\dot\epsilon_1^2(t)+\dot\epsilon_2^2(t)+\frac{2\overline r}{1+\overline r}\dot\epsilon_1(t)\dot\epsilon_2(t)}dt\)

\(\theta={\rm Tan}^{-1}\dot\gamma={\rm Tan}^{-1}\frac{\dot\epsilon_2}{\dot\epsilon_1}\)

  \(\overline r=\frac{r_0+2r_{45}+r_{90}}{4}\)

극좌표계 성형한계도 상에서 변형경로를 표현하는 방법은 기존 성형한계도와는 조금 다른데, 이를 아래 그림들에 표현하였다. 예를 들어 다음과 같이 양축인장(biaxial tension)에서 출발하여 유효소성변형률(EPS) 0.3 점에서 다시 단축인장(unaxial tension)으로 변형이 되어 성형한계에 도달했다고 하자. 이 경우는 비례부하(proportional loading)가 아니므로 파단변형률은 초기 선도(청색) 대비 다른 형태(적색)을 띠게 된다.

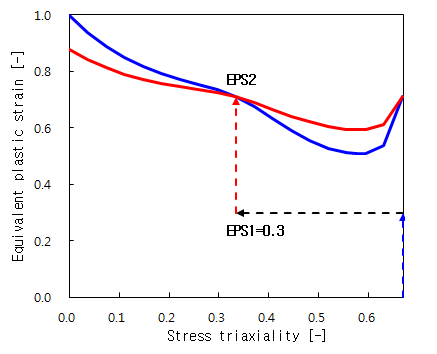응력삼축성 vs 파단변형률

기존 성형한계도 상에서 변형 경로 진행은 아래 그림과 같이, 원점에서 각도 \(\theta_1\)으로 출발하여 \((\epsilon_2,\,\epsilon_1)=(0.15, 0.15)\) 점에서 다시 각도 \(\theta_2\)로 다음 변형이 시작되어 성형한계에 이르게 된다. 마찬가지로 성형한계도는 초기 선도(청색) 대비 다른 형태(적색)를 가진다.

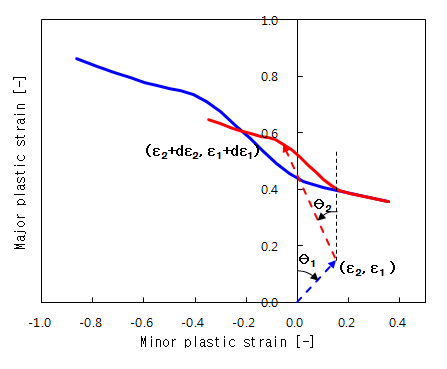변형률 성형한계도(strain FLD)

이에 반해 극좌표계 성형한계도에서는 아래 그림과 같이, 원점에서 변형경로가 시작되는 것은 동일하지만 \(f(\epsilon_2,\,\epsilon_1)\) 점과 동일한 \(\overline{\epsilon_p}\) 선상에서 다음 경로와 같은 각도 \(\theta_2\)를 갖는 점에서 다음 경로가 시작된다. 극좌표계 성형한계도 내에서는 기존 성형한계도와 달리 사전변형에 의한 여러 성형한계도가 한 개의 선으로 모이게 된다. 이러한 특성 때문에 극좌표계 성형한계도는 변형경로에 무관한 비선형(non-linear) 성형한계도의 성격을 지니게 된다. 이것은 \(\overline{\epsilon_p}\)를 도입하여 성형한계를 표현하는 특성 상, 성형경로가 변하더라도 일정하게 유지 되기 때문이다. 또한 기존 성형한계도와 형태가 비슷하기 때문에 사용자가 익숙하게 접근할 수 있고, 사용법도 크게 다르지 않기 때문에 큰 혼란없이 사용할 수 있다.      

극좌표계 성형한계도(polar EPS FLD)