타원공 주의의 응력 (Stess around Elliptical Hole)

복소함수 (Complex Functions)

실제적인 많은 문제들에 있어서 두 변수의 복소함수(complex function)를 응력함수(stress function)로 사용하는 것이 편리하다. 복소함수는 지배 방정식을 자동으로 만족시키는 능력이 있으며, 단지 경계조건을 만족하기 위한 조정이 필요하다. 이러한 이유로 복소변수법(complex-variable methods은 이론적인 응력해석에 있어서 중요한 역할을 하므로, 본 글과 같은 입문서에서도 그 방법론을 기술한다. 몇가지 필요한 관계들을 도입하기 위해 복소평면 x와 y, 또는 오일러 공식에 의한 극좌표계 상의 복소수(complex number) z를 생각한다.

\(z=x+iy=re^{i\theta}\)

여기서 \(i=\sqrt{-1}\) 이다. 임의의 해석함수(analytic function) f(z)는 그의 미분이 z에만 의존하고, 다음과 같은 형태를 취한다.

\(f(z)=\alpha+i\beta\)

여기서 α와 β는 x와 y의 실함수이다. α와 β는 코시-리만 방정식을 만족함을 쉽게 보일 수 있다:

\(\dfrac{\partial\alpha}{\partial x}=\dfrac{\partial\beta}{\partial y}\qquad\dfrac{\partial\alpha}{\partial y}=\dfrac{\partial\beta}{\partial x}\)

위의 첫번째 식을 x에 대하여 그리고 두번째 식을 y에 대하여 미분하면 다음과 같은 결과를 얻는다.

\(\dfrac{\partial^2\alpha}{\partial x^2}+\dfrac{\partial^2\alpha}{\partial y^2}\equiv\nabla^2\alpha=0\)

이 식은 라플라스 방정식(Laplace's equation)이라 하고, 이 방정식을 만족하는 함수를 조화(harmonic) 함수라 칭한다. 동일하게 α 대신에 β를 쓰면 \(\nabla^2\beta=0\)를 얻으므로, 복소함수의 실수부와 허수부, 둘 다 라플라스 방정식의 해가 된다. 이제 xψ 형태의 함수, 여기서 ψ는 조화함수, 를 생각한다; 이 함수를 직접 미분하면 다음 식이 성립함을 보일 수 있다.

\(\nabla^4(x\psi)=\nabla^2\left\{\nabla^2(x\psi)\right\}=\nabla^2\left(\dfrac{\partial\psi}{\partial x}\right)=0\)

즉, ψ가 조화함수인, xψ 형태의 어떠한 함수도 호환 방정식(compatibility equation)을 만족하므로 응력함수로 사용할 수 있다. 유사하게 yψ와 \((x^2+y^2)\psi=r^2\psi\)도 ψ 자신과 같이 응력함수로 적합함을 보일 수 있다. 일반적으로 적합한 응력함수는 임의의 두 해석함수 ψ와 χ로부터 다음과 같이 얻을 수 있다.

\(\begin{split}\Phi&={\rm Re}\left\{(x-iy)\psi(z)+\chi(z)\right\}\\&=x{\rm Re}\psi(z)+y{\rm Im}\psi(z)+{\rm Re}\chi(z)\end{split}\)

여기서 "Re"와 "Im"은 각각 이 복소 표현식의 실수부와 허수부를 의미한다. 이 함수 Φ를 응력함수에 대입하고 코시-리만 방정식을 활용하면 이에 해당하는 응력들을 아래와 같이 얻게 된다.

\(\begin{split}&\sigma_{xx}=\dfrac{\partial^2\Phi}{\partial y^2}=-x{\rm Re}\psi''(z)+2{\rm Re}\psi'(z)-y{\rm Im}\psi''(z)-{\rm Re}\chi''(z)\\&\sigma_{yy}=\dfrac{\partial^2\Phi}{\partial x^2}=\ \ \ x{\rm Re}\psi''(z)+2{\rm Re}\psi'(z)+y{\rm Im}\psi''(z)+{\rm Re}\chi''(z)\\&\tau_{xy}=-\dfrac{\partial^2\Phi}{\partial x\partial y}=x{\rm Im}\psi''(z)-y{\rm Re}\psi''(z)+{\rm Im}\chi''(z)\end{split}\)

또한 이들 사이의 다음 관계식을 얻는다.

\(\begin{split}\sigma_{xx}+\sigma_{yy}&=4{\rm Re}\psi'(z)\\\sigma_{yy}-\sigma_{xx}+2i\tau_{xy}&=2\left\{\bar z\psi''(z)+\chi''(z)\right\}\end{split}\)

여기서 따옴표(primes)는 z에 관한 미분을 나타내고, 윗줄(overbar)은 i를 -i로 치환한 켤레 함수(conjugate function)를 나타낸; 따라서

\(\bar z=x-iy\)

위의 (x, y) 직교좌표계의 응력 성분들은 아래식을 통하여 (α, β) 직교곡선좌표계(orthogonal curvillinear coordinates)로 변환될 수 있다.

\(\begin{split}\sigma_{\alpha\alpha}+\sigma_{\beta\beta}&=\sigma_{xx}+\sigma_{yy}\\\sigma_{\beta\beta}-\sigma_{\alpha\alpha}+2i\tau_{\alpha\beta}&=\left(\sigma_{yy}-\sigma_{xx}+2i\tau_{xy}\right){\rm e}^{2i\gamma}\end{split}\)

여기서 \(\sigma_{\alpha\alpha}\)는 α=일정 곡선 상의 수직성분, \(\sigma_{\beta\beta}\)는 β=일정 곡선 상의 수직성분 및 \(\tau_{\alpha\beta}\)는 두 곡선의 전단성분이다. 그리고 γ는 β=일정 곡선과 x축이 이루는 각도이다.

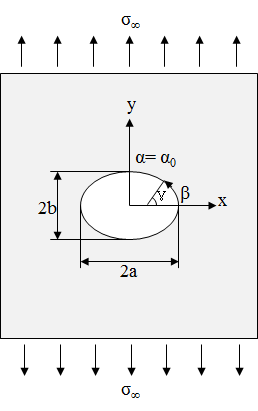
타원공 주위의 응력 (Stresses around an Elliptical Hole)

파과이론에 있어서 매우 중요한 발전으로, 잉글리스(Inglis)는 커쉬의 해법을  확장하여 원형공(circular hole)이 아닌 타원공(elliptical hole)을 포함한 평판의 응력장을 다루기 위해 복소 포텐셜 함수(complex potential function)를 사용하였다. 이것은 타원의 단축을 작게 함으로서 균열(crack)과 유사한 형상을 취급할 수 있다. 이 경우 아래와 같이 정의되는 α, β 타원좌표계를 사용하는 것이 편리하다.

\(x=c\cosh\alpha\cos\beta,\qquad y=c\sinh\alpha\sin\beta\)

여기서 c는 상수이다. β를 소거하면 결과적으로 다음과 같이 등가로 나타낼 수 있다.

\(\dfrac{x^2}{\cosh^2\alpha}+\dfrac{y^2}{\sinh^2\alpha}=c^2\)

타원의 경계에서는 \(\alpha=\alpha_0\) 이므로

\(c\cosh\alpha_0=a,\qquad c\sinh\alpha_0=b\)

로 쓸 수 있다. 여기서 a와 b는 상수이다. 그러면 경계에서는

\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)

직교좌표계에서 주반경과 부반경이 a와 b인 타원의 방정식임을 알 수 있다. 이 타원좌표계는 복소변수(complex variable)의 항으로 다음과 같이 쓸 수 있다.

\(z=c\cosh\zeta,\qquad\zeta=\alpha+i\beta\)

타원의 경계를 가로질러, \(\alpha\)는 \(\alpha_0\)로 일정한 반면에 \(\beta\)는 0에서 2π로 변화한다. 그러므로 응력은 \(\beta\)에 대하여 2π의 주기를 가져야 하고, 타원에서 멀리 떨어진 곳에서는 원거리 단축응력 상태 \(\sigma_{yy}=\sigma_{\infty},\ \sigma_{xx}=\tau_{xy}=0\)가 된다; 그러면 앞의 응력 간의 관계식으로부터 다음식을 얻는다.

\(\zeta\rightarrow\infty\begin{cases}4{\rm Re}\psi'(z)&=\sigma_\infty\\2\left\{\bar z\psi''(z)+\chi''(z)\right\}&=\sigma_\infty\end{cases}\)

이들 경계조건은 아래 형태의 포텐셜 함수로 만족될 수 있다.

\(\begin{split}&4\psi(z)=Ac\cosh\zeta+Bc\sinh\zeta\\&4\chi(z)=Cc^2\zeta+Dc^2\cosh2\zeta+Ec^2\sinh2\zeta\end{split}\)

여기서 A, B, C, D, E는 경계조건으로 결정되는 상수들이다. 이제 이 상수들을 구하기 위해 위의 복소함수들의 도함수를 합성함수의 미분법으로 아래와 같이 구한다.

\(\begin{split}\psi'(z)&={1\over4}(A+B\coth\zeta)\\\chi'(z)&={c\over4}{\rm csch}\zeta(C+2D\sinh2\zeta+2E\cosh2\zeta)\\\psi''(z)&=-{B\over4c}{\rm csch}^3\zeta\\\chi''(z)&={1\over4}{\rm csch}^3\zeta\left\{-C\cosh\zeta+4D\sinh^3\zeta+2E\cosh\zeta\left(2\sinh^2\zeta-1\right)\right\}\end{split}\)

또한 이들을 앞의 응력 관계식에 대입하기 위해 다음식을 구한다.

\(\bar z\psi''(z)+\chi''(z)=\dfrac{1}{4}{\rm csch}^3\zeta\left\{-B\cosh\bar\zeta-C\cosh\zeta+4D\sinh^3\zeta+2E\cosh\zeta\left(2\sinh^2\zeta-1\right)\right\}\)

이제 이 식들을 응력식에 대입하여 정리하면 다음과 같다.

\(\begin{split}&\sigma_x+\sigma_y={1\over2}\left\{\left(A+\bar A\right)+\left(B\coth\zeta+\bar B\coth\bar\zeta\right)\right\}\\&\sigma_y-\sigma_x+2i\tau_{xy}={1\over2}{\rm csch}^3\zeta\left\{-B\cosh\bar\zeta-C\cosh\zeta+4D\sinh^3\zeta+2E\cosh\zeta\left(2\sinh^2\zeta-1\right)\right\}\end{split}\)

먼저 위의 식을 원거리 경계조건을 적용하고 \(\zeta\rightarrow\infty\) 일 때 \(\coth\zeta\rightarrow1,\ \cosh\zeta\,\rm csch^3\zeta\rightarrow0\) 를 생각하면 다음 관계를 얻는다.

\({\rm Re}(A+B)=\sigma_\infty,\ 2(D+E)=\sigma_\infty\)

앞의 식에서 보듯이 A의 허수부 Im A는 응력의 기여가 없고 강체운동을 유발하는 정도이다. 따라서 Im A=0으로 놓고 다음과 같이 취한다.

\(A={\rm Re}A,\ B=B_1+iB_2,\ C=C_1+iC_2,\ D=D_1+iD_2,\ E=E_1+iE_2\)

여기서 \(A,\,B_1,\,B_2,\,B_2,\,C_1,\,C_2,\,D_1,\,D_2,\,E_1\) 및 \(E_2\)는 실수들이다. 이 식들을 앞의 경계조건 식에 대입하면 아래 식들이 나온다.

\(A+B_1=\sigma_\infty,\ 2(D_1+E_1)=\sigma_\infty,\ 2(D_2+E_2)=0\qquad(1)\)

두번째로 응력성분들은 타원좌표계로 표현하면 \(z=f(\zeta)=c\cosh\zeta\) 이고

\({\rm e}^{2i\gamma}=\dfrac{f'(\zeta)}{f'(\bar\zeta)}=\dfrac{\sinh\zeta}{\sinh\bar\zeta}\)

이므로 직교좌표계의 응력식으로부터 다음과 같이 된다.

\(\begin{split}\sigma_{\alpha\alpha}+\sigma_{\beta\beta}&=4{\rm Re}\psi'(z)\\\sigma_{\beta\beta}-\sigma_{\alpha\alpha}+2i\tau_{\alpha\beta}&=2\left\{\bar z\psi''(z)+\chi''(z)\right\}\dfrac{\sinh\zeta}{\sinh\bar\zeta}\end{split}\)

위의 첫번째식에서 두번째식을 차감하면

\(\sigma_{\alpha\alpha}-i\tau_{\alpha\beta}=2{\rm Re}\psi'(z)-\left\{\bar z\psi''(z)+\chi''(z)\right\}\dfrac{\sinh\zeta}{\sinh\bar z}\)

윗식에 포텐셜 함수식을 대입하고, 타원공 경계(\(\alpha=\alpha_0\))에서는 \(\sigma_{\alpha\alpha}=\tau_{\alpha\beta}=0\) 이므로 이 조건에서 다음식이 유도된다.

\(\left\{(2A+B\coth\zeta)\sinh\bar\zeta+(\bar B+B{\rm csch}^2\zeta)\cosh\bar\zeta+(C+2E){\rm csch}^2\zeta\cosh\zeta-4D\sinh\zeta-4E\cosh\zeta\right\}_{\alpha=\alpha_0}=0\)

그리고 \(\alpha=\alpha_0\) 이면

\(\zeta+\bar\zeta=2\alpha_0\). 즉, \(\bar\zeta=2\alpha_0-\zeta\).

이다. 그러면 앞의 식은 다음과 같이 정리된다.

\(\begin{split}&(2A\sinh2\alpha_0-B\cosh2\alpha_0+\bar B\cosh2\alpha_0-4E)\cosh\zeta\\&+(B\sinh2\alpha_0-2A\cosh2\alpha_0-\bar B\sinh2\alpha_0-4D)\sinh\zeta\\&+(B\cosh2\alpha_0+C+2E){\rm csch}^2\zeta\cosh\zeta=0\end{split}\)

여기서 ζ는 \(\alpha=\alpha_0\) 조건을 만족하는 임의의 값이다. 따라서 다음식들이 필연적으로 성립한다.

\(\begin{cases}2A\sinh2\alpha_0-B\cosh2\alpha_0+\bar B\cosh2\alpha_0-4E=0\\B\sinh2\alpha_0-2A\cosh2\alpha_0-\bar B\sinh2\alpha_0-4D=0\\B\cosh2\alpha_0+C+2E=0\end{cases}\)

앞의 상수들을 실수부와 허수부로 분해한 식들을 대입하고 양변의 계수들을 비교하면 다음식들을 얻는다.

\(\begin{cases}A\sinh2\alpha_0-2E_1=0,\ 2E_2+B\cosh2\alpha_0=0\\A\cosh2\alpha_0+2D_1=0,\ B_2\sinh2\alpha_0-2D_2=0\\B_1\cosh2\alpha_0+C_1+2E_1=0\\B_2\cosh2\alpha_0+C_2+2E_2=0\end{cases}\qquad(2)\)

앞의 식 (1)과 위의 (2)식으로부터 9개의 미지수 \(A~E_2\)에 대한 9개의 식으로 구성된 연립방정식을 조합할 수 있다. 이 방정식들로부터 다음 상수값들을 얻는다.

\(\begin{cases}A=-\sigma_\infty{\rm e}^{2\alpha_0}\\B_1=\sigma_\infty\left(1+{\rm e}^{2\alpha_0}\right)\\B_2=0\\C_1=-\sigma_\infty(\cosh2\alpha_0+1)\\C_2=0\\D_1=\dfrac{\sigma_\infty}{2}{\rm e}^{2\alpha_0}\cosh2\alpha_0\\D_2=0\\E_1=-\dfrac{\sigma_\infty}{2}{\rm e}^{2\alpha_0}\sinh2\alpha_0\\E_2=0\end{cases}\)

위에서 결정된 모든 상수들을 대입하면 복소 포텐셜은 다음과 같이 주어진다.

\(\begin{split}&4\psi(z)=\sigma_\infty\left\{\left(1+{\rm e}^{2\alpha_0}\sinh\zeta-{\rm e}^{2\alpha_0}\cosh\zeta\right)\right\}\\&4\chi(z)=-\sigma_\infty c^2\left\{(\cosh2\alpha_0-\cosh\pi)\zeta-{1\over2}{\rm e}^{2\alpha_0}\cosh2\left(\zeta-\alpha_0-i{\pi\over2}\right)\right\}\end{split}\)

이 식들을 이용하여 앞의 응력함수와 응력성분의 관계식을 이용하면 \(\sigma_{xx},\,\sigma_{yy}\) 및 \(\tau_{xy}\)를 얻을 수 있다. 하지만 이들 대입과정의 계산량은 가볍게 볼 수 없으며, 컴퓨터가 통용되기 전에는 잉글리스의 해법이 균열 선단 근처의 응력장을 조사하기 위해 제한적으로 사용되었다.

y방향 단축응력을 받는 타원공 부근의 응력장 (a) \(\sigma_{yy}\) 분포도, (b) \(\sigma_{xx}\) 분포도

위의 그림은 잉글리스 방정식의 응력 분포를 보여준다. 예상대로 구멍 주변에 \(\sigma_{yy}\)의 강한 응력집중이 관찰된다. 이곳의 횡방향 응력 \(\sigma_{xx}\)은 경계조건을 만족해야 하므로 영이 된다. 하지만 구멍으로부터 약간 떨어진 곳에서 (\(\sigma_{yy}\)의 1/15로 밝혀진) 완만한 응력집중을 보인다. 재료가 목재 또는 생물학적 구조의 섬유 사이와 같이 y방향 취약면이 있다면, \(\sigma_{xx}\) 응력이 원인이 된 틈이 주 균열 선단에서 y방향으로 열리게 된다. 이것이 균열을 둔화시키고 막아, 재료에 인성을 부여하게 된다. 이 효과를 쿡-고든 강화기구(Cook-Gordon toughening mechanism)라고도 한다.

타원공 경계면에서는 수직응력 \(\sigma_{\alpha\alpha}\)이 작용하지 않으므로 잉글리스 해법은 간단해 진다. 그러면 접선응력 성분이 직접 계산될 수 있다.

\(\left(\sigma_{\beta\beta}\right)_{\alpha=\alpha_0}=\sigma_\infty{\rm e}^{2\alpha_0}\left\{\dfrac{\sinh2\alpha_0\left(1+{\rm e}^{-2\alpha_0}\right)}{\cosh2\alpha_0-\cos2\beta}-1\right\}\)

응력의 최대치는 장축의 끝단에서 발생(cos 2β=1) 하고 \(\tanh\alpha_0=b/a\) 이므로 다음식과 같다:

\(\left(\sigma_{\beta\beta}\right)_{\beta=0,\pi}=\sigma_{yy}=\sigma_\infty\left(1+2\dfrac{a}{b}\right)\)

또한 이 식은 장축 끝단의 곡률반경 \(\rho=b^2/a\)의 항으로 아래와 같이 쓸 수 있다.

\(\sigma_{yy}=\sigma_\infty\left(1+2\sqrt{\dfrac{a}{\rho}}\right)\)

이 결과는 자체로 유용하다: 큰 균열이 작은 것보다 분명히 불리(국부응력은 균열크기 a에 따라 증가)하고 날카로운(ρ 감소) 기공(void) 또한 둥근 것보다 좋지 않다는 것은 명백하다. 더우기 균열이 날카로워 지면(ρ→0) 응력 \(\sigma_{yy}\)가 무한대로 커지므로, 응력집중의 개념은 매우 날카로운 균열에서는 사용이 어려워진다. 타원의 장축과 단축이 같을 때(a=b)의 결과는 원형공(circular hole)의 경우와 동일해진다.