가설검정

개요

가설검정이란 설정된 가설(귀무가설)이 옳다고 할 때, 표본에서 통계량을 사용하여 얻은 값(검정통계치)과 통계량의 이론적 분포에서 얻어지는 어떤 특정값(임계치)을 비교하여 그 가설을 기각할 것인가 또는 채택할 것인가를 판정하는 것이다.

모수에 대한 주장을 시각적으로 판단하기 어려우므로 가설검정을 통해 주관적인 판단이 아닌 객관적인 의사결정을 할 수 있도록 한다. 이 때 오류의 가능성에 대해서 사전에 오류의 허용확률을 정해 놓고 가설의 채택이나 기각을 결정한다.

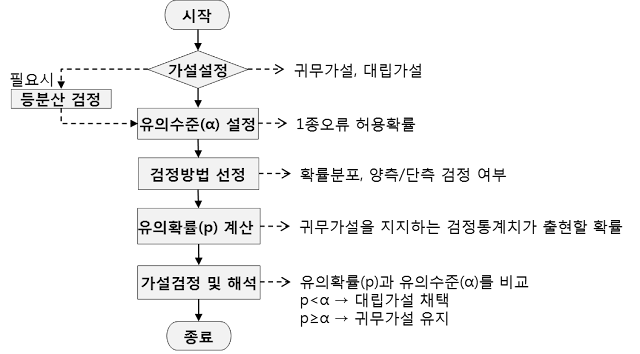
절차

귀무가설과 대립가설

귀무가설 \((\text H_0)\)

모집단의 모수에 대해서 현재까지 알려진 사실을 기준으로 설정한 가설이다. 예를 들면 '차이가 없다', '효과가 없다', '~ 같다'등으로 표현된다.

대립가설 \((\text H_1)\)

귀무가설과 반대되는 것으로 새롭게 주장하고자 하는 가설이다. 귀무가설과 배타적이며 동시에 성립할 수 없다. '차이가 있다', '효과가 있다', '모두 같지는 않다' 등으로 표현된다. 

가설검정은 모수의 차이 여부를 판단하는 것으로 귀무가설(차이가 없다)과 대립가설(차이가 있다)는 가설검정의 결과로 나올 수 있는 2가지 진술을 나타낸다.

유무죄 판결과 가설검정

유무죄 판결	'죄가 없다.'(귀무가설)고 가설을 정하고, '죄가 있다.'(대립가설)은 증거를 수집하여 범죄여부를 입증하고 법률로써 판단한다.
통계적 가설검정	'모집단의 평균이 차이가 없다.'(귀무가설)고 가설을 정하고, '모집단의 평균이 차이가 있다.'(대립가설)는 표본의 통계치를 계산하여 얻은 유의확률을 유의수준과 비교하여 판단한다.

가설검정 오류

1종오류와 2종오류

표본에서 계산된 통계치를 이용하여 가설의 채택/기각 여부를 판정하므로 오류가 발생한다. 이 오류에 의해 잘못된 결론을 내릴 수 있다.

가설검정에서 귀무가설을 채택 또는 기각하는 경우 두가지 오류 중 하나를 범할 가능성이 있다.

1) 1종오류 : 귀무가설이 맞는 데, 잘못하여 기각하는 경우
2) 2종오류 : 귀무가설이 틀린 데, 잘못하여 채택하는 경우

가설검정에서는 1종오류만을 고려한다.

구분		귀무가설
		참	거짓
귀무가설	채택	정확한 결론 ( 1-α )	2종오류 ( β )
	기각	1종오류 ( α )	정확한 결론 ( 1-β )

유의수준과 유의확률

유의수준 (α)

귀무가설은 맞는 사실인데 이를 잘못 기각하여 대립가설을 채택하는 1종오류에 대한 최대 허용확률을 말한다. 일반적으로 0.05를 많이 사용한다. (그 외에 0.1, 0.01도 사용한다.)

임계치

주어진 유의수준에서 귀무가설의 채택 또는 기각을 결정하는데 사용되는 기준값이다. 사용할 확률분포와 유의수준이 결정되면 임계치는 자동적으로 정해진다.

검정통계치

귀무가설의 채택 또는 기각 여부를 결정하기 위해 표본을 통해 계산된 값이다.

유의확률 (p)

귀무가설이 참일 때 귀무가설을 지지하는 검정통계치가 출연할 확률로 적용할 확률분포와 검정통계치가 결정되면 유의확률은 자동적으로 정해진다.

채택역과 기각역

채택역

검정통계치가 발생할 확률이 유의수준보다 큰 영역으로 귀무가설 영역이 된다.

기각역

검정통계치가 발생할 확률이 유의수준보다 작은 영역으로 대립가설 영역이 된다.

양측검정과 단측검정

대립가설의 형태에 따라 결정된다.

1) 양측검정 : 가설검정에서 귀무가설을 기각할 영역(대립가설을 채택할 영역)이 양쪽에 위치한다.
2) 단측검정 : 가설검정에서 귀무가설을 기각할 영역(대립가설을 채택할 영역)이 한쪽에 위치한다.

유형	양측검정	단측검정
		좌측검정	우측검정
귀무가설	\(H_0:\mu=\mu_0\)	\(H_0:\mu=\mu_0\)	\(H_0:\mu=\mu_0\)
대립가설	\(H_1:\mu\ne\mu_0\)	\(H_1:\mu<\mu_0\)	\(H_1:\mu>\mu_0\)

확률분포상 표시

양측검정과 단측검정의 차이

대립가설의 형태에 따라 귀무가설 영역(채택역)과 대립가설 영역(기각역)이 결정된다.

양측검정			대립가설 :~의 차이가 0 이 아니다. (~의 차이가 0 보다 크거나 작다.)
단측검정	좌측검정		대립가설 :~의 차이가 0 보다 작다.
	우측검정		대립가설 :~의 차이가 0 보다 크다.

검정에 사용되는 확률분포

데이터	검정항목	표준편차	확률분포
계량치 (연속형)	1개의 모평균	안다.	정규분포
		모른다.	t-분포
	독립적인 2개의 모평균 차	안다.	정규분포
		모른다.	t-분포
	대응관계의 2개의 모평균 차	안다.	정규분포
		모른다.	t-분포
	2개의 모분산 차	-	F-분포
계수치 (이산형)	1개의 모불량률	np≥5 이고 n(1-p)≥5	정규분포
		np＜5 또는 n(1-p)＜5	이항분포
	2개의 불량률 차	n1, n2가 크다.	정규분포
	1개의 모결점수	m≥5	정규분포
		m＜5	포아송 분포
	2개의 모결점수 차	m1, m2≥5	정규분포

[예제 1] (1표본 t-검정) A-엔진의 공인출력이 112PS로 알려져 있고 실측출력이 아래와 같을 때 공인출력과 차이가 있는지 판정하라.

실측출력 (PS)

114.2

115.4

110.9

110.9

122.1

113.1

115.4

109.8

1) 가설설정

- 귀무가설\((H_0)\) : 실측출력은 112PS 이다. \((\mu_0-112=0)\)
- 대립가설\((H_1)\) : 실측출력은 112PS가 아니다. \((\mu_0-112\ne0)\)

2) 유의수준 α=0.05

3) 검정방법

- 공인출력과 실측출력 평균이 차이가 있는지 보는 것이므로 평균을 검정한다.
- 표본의 개수가 8개(<30)이므로 확률분포는 t-분포를 사용한다.
- 대립가설이 \(\mu_0\ne\mu\) 이므로 양측검정을 사용한다.

4) 검정통계치 계산

실측출력 평균 : \(\overline X=\frac{\sum_{i=1}^8X_i}{n}=113.975\), 표준편차 : \(S=\sqrt{\frac{\sum_{i=1}^8(X_i-\overline X)^2}{n-1}}=3.914\)
실측출력의 표준오차 : \(SE=\frac{S}{\sqrt{n}}=1.384\)
검정통계치 : \(T=\frac{\overline X-\mu}{S/\sqrt{n}}=1.43\)

5) 유의확률 계산 : P(|t|>1.43)=0.197>0.05

유의확률(0.197)이 유의수준(0.05) 보다 크므로 채택역에 검정통계치가 존재한다. 따라서 귀무가설을 채택한다. 즉, 실측출력은 공인출력과 차이가 없다.

[예제 2] (2표본 t-검정) 동일 시험조건 하에서 엔진 A와 엔진 B의 계측된 출력(PS)에 대해 시험결과가 다음과 같을 때 두 엔진이 출력차이가 있는 지 판정하라. 단, 해당 가설을 유의수준 5%에서 검정한다.

엔진 A	88	92	81	85	93	81	86	82	94	86	87	83
엔진 B	88	87	79	77	93	77	76	85	72	76	85	91

1) 가설설정

- 귀무가설 \((H_0)\) : 엔진 A와 엔진 B는 출력 차이가 없다. \((\mu_A-\mu_B=0)\)
- 대립가설 \((H_1)\) : 엔진 A와 엔진 B는 출력 차이가 있다. \((\mu_A-\mu_B≠0)\)

2) 유의수준 설정 : α=0.05

3) 검정방법 : 평균의 차이를 검정하는 것이며 데이터가 12개(<30)이므로 확률분포는 t-분포를 사용한다. 대립가설이 \(\mu_A-\mu_B\ne0\) 이므로 양측검정이다.

4) 검정통계치 계산

평균 : \(\overline X_A=86.500,\), \(\overline X_B=82.167\), 분산 : \(S_A^2=20.636\), \(S_B^2=46.515\)
공동분산 : \(S_{Pooled}^2=\frac{(n_A-1)S_A^2+(n_B-1)S_B^2}{n_A+n_B-2}=33.576\)
검정통계치 : \(T=\frac{(\overline X_A-\overline X_B)-(\mu_A-\mu_B)}{S_{Pooled}\sqrt{{1\over n_A}+{1\over n_B}}}\sim t(n_A+n_B-2)=1.83\)

5) 유의확률 계산 : P(|t|>1.83)=0.08>0.05

유의확률(0.08)이 유의수준(0.05) 보다 크므로 채택역에 검정통계치가 존재한다. 따라서 귀무가설을 채택한다. 즉, 엔진 A와 B는 출력 차이가 없다.

2표본 t-검정 시 T-통계량 계산식

표본의 크기가 작으며, 두 모분산이 다를 경우

\(T=\frac{(\overline X_1-\overline X_2)-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}\sim t(n_0)\qquad n_0=\frac{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)^2}{\frac{\left(\frac{S_1^2}{n_1}\right)^2}{n_1-1}+\frac{\left(\frac{S_2^2}{n_2}\right)^2}{n_2-1}}\) (소수점이하 버림)

표본의 크기가 작으며, 두 모분산이 같을 경우

\(T=\frac{(\overline X_1-\overline X_2)-(\mu_1-\mu_2)}{S_{Pooled}\sqrt{{1\over n_1}+{1\over n_2}}}\sim t(n_1+n_2-2)\qquad S_{Pooled}=\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}}\)