F-분포 (F-distribution)
\(X_1,\,X_2,\,\cdot\cdot\cdot,\,X_{n1}\)과 \(Y_1,\,Y_2,\,\cdot\cdot\cdot,\,Y_{n2}\)가 각각 정규 모집단 \(N(\mu_1,\,\sigma_1^2),\,N(\mu_2,\,\sigma_2^2)\) 으로부터 추출된 표본크기 \(n_1,\,n_2\)의 서로 독립인 확률표본일 때, 다음 확률변수 F는 자유도 \((n_1-1,\,n_2-1)\)인 F-분포를 따른다.
\(F=\dfrac{S_1^2}{\sigma_1^2}/\dfrac{S_2^2}{\sigma_2^2}=\left(\dfrac{S_1^2}{S_2^2}\right)/\left(\dfrac{\sigma_1^2}{\sigma_2^2}\right)\)
여기서
\(\begin{align}&\overline X={1\over n}\sum_{i=1}^{n_1}X_i\qquad S_1^2=\frac{\begin{align}\sum_{i=1}^{n_1}\end{align}\left(X_i-\overline X\right)^2}{n_1-1}\\&\overline Y={1\over n}\sum_{i=1}^{n_2}Y_i\qquad S_2^2=\frac{\begin{align}\sum_{i=1}^{n_2}\left(Y_i-\overline Y\right)^2\end{align}}{n_2-1}\end{align}\)
특징
표본분산의 비를 나타내는 분포이다. 확률변수의 분자, 분모에 포한된 자유도\((n_1-1,\,n_2-1)\)에 따라 분포의 형태가 달라 지며 \(X\sim F(n_1-1,\,n_2-1)\)로 표시한다. 왼쪽으로 치우친 분포이지만 자유도가 증가할 수록 대칭 분포에 근접한다. 등분산 검정 / 분산분석 / 실험계획법 등에 사용한다.
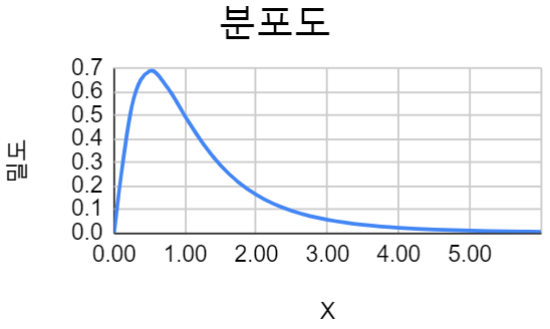 |
| F-분포, \(d_1=5, d_2=10\) |
필자도 통계 전공이 아니고 인자의 유의성이나 중요도만 평가하면 그만이라 그 과정을 알 필요는 없다. 하지만 과거 컴퓨터가 없었던 시절에는 직접 계산을 했을 것이고 지적 호기심이 있어서 그 과정을 계산해 보았다.
먼저 F-분포의 확률 밀도함수는
\(f(x;d_1,d_2)=\dfrac{\sqrt{\dfrac{(d_1x)^{d_1}d_2^{d_2}}{(d_1x+d_2)^{d_1+d_2}}}}{xB\left({d_1\over2},{d_2\over2}\right)},\ \text{베타함수}\ B\left({d_1\over2},{d_2\over2}\right)=\int_0^1t^{d_1/2-1}(1-t)^{d_2/2-1}dt\)
이제 분산분석 글 예제의 F-비 값, 0.006621에 대한 P-값을 구해 보자. 자유도 \(d_1=1,\,d_2=18\) 이므로 베타 함수는
\(B\left({1\over2},{18\over2}\right)=\int_0^1t^{-{1\over2}}(1-t)^8dt\approx0.59908\)
확률밀도함수는
\(f(x,1,18)=\frac{\sqrt{\frac{18^{18}x}{(x+18)^{19}}}}{0.59908x}\)
P-값은 확률밀도함수의 x=F-비 오른쪽 면적이므로
\(F(x)=\int_x^\infty f(x)dx,\qquad F(0.006621)=\int_{0.006621}^\infty\frac{\sqrt{\frac{18^{18}x}{(x+18)^{19}}}}{0.59908x}=0.936041\)
계사된 P-값은 0.936041 이고 엑셀 분석도구 P-값은 0.936046이다. 엑셀을 이용할 때는 통계함수 F.DIST.RT(x,d1,d2)나 '데이터-데이터 분석-분산분석'을 쓰면 된다.



댓글
댓글 쓰기