순수전단 (Pure Shear)

순수전단이란 물체가 3차원적으로 균일하게 납작해지는 변형을 말한다. 이것은 아래 그림과 같이 물체가 한 방향으로 늘어나는 동시에 수직방향은 줄어드는 비회전 변형률의 예이다. 고무와 같은 연성 재질의 순수전단은 종종 초탄성(hyperelastic) 및 파괴역학(fracture mechanical) 거동을 특성화하기 위해 사용된다. 순수전단은 강체회전(rigid body rotation)을 수반하지 않는다는 점에서 단순전단(simple shear)과는 다르다.

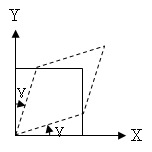순수전단

위의 그림과 같은 순수전단의 변형 후 위치벡터 p(x, y) 각 성분은 다음과 같이 정의된다.

\(\begin{split}x=X+\gamma Y\\y=\gamma X+Y\end{split}\)

따라서 변형구배(deformation gradient)는 다음과 같이 대칭행렬이며 이것은 강체회전이 없다는 것을 의미한다.

\({\bf F}=\begin{bmatrix}\frac{\partial x}{\partial X}&\frac{\partial x}{\partial Y}\\\frac{\partial y}{\partial X}&\frac{\partial y}{\partial Y}\end{bmatrix}=\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}\)

위의 결과로부터 그린변형률(Green strain)을 정의에 따라 구할 수 있다.

\(\begin{split}{\bf E}&={1\over2}({\bf F}^T\cdot {\bf F}-{\bf I})\\&={1\over2}\left\{\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}-\begin{bmatrix}1&0\\0&1\end{bmatrix}\right\}\\&={1\over2}\left\{\begin{bmatrix}1+\gamma^2&\gamma\\\gamma&1+\gamma^2\end{bmatrix}-\begin{bmatrix}1&0\\0&1\end{bmatrix}\right\}\\&={1\over2}\begin{bmatrix}\gamma^2&2\gamma\\2\gamma&\gamma^2\end{bmatrix}\end{split}\)

이것 역시 회전이 발생하지 않았으므로 변형률 텐서의 비대각 성분(off-diagonal)이 같음을 알 수 있다. 변형이 작을 경우 \(\gamma^2\approx0\) 이므로 위의 그린변형률의 선형 근사(linear approximation)는 미소변형률 텐서(small strain tensor)가 된다.

\(\boldsymbol{\epsilon}=\begin{bmatrix}\frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}\\\frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}\end{bmatrix}=\begin{bmatrix}0&\gamma\\\gamma&0\end{bmatrix}\)

여기서는 단지 전단성분(shearing components)만이 존재한다.