부정정보(Statically Indeterminate Beams)

반력(reactions)의 개수가 정적 평형(static equilibrium)의 방정식으로부터 구할 수 있는 것보다 많은 보(beam)를 부정정(statically indeterminate) 보라 부르고, 분석을 위해서는 처짐(deflection)의 계산이 요구된다.

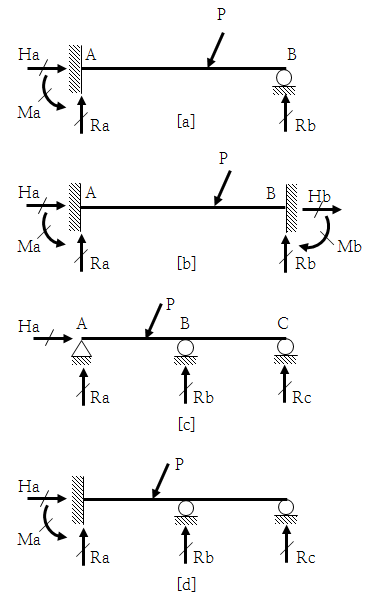
위의 그림에 몇가지 형태의 부정정 보가 도시되어 있다. 그림 [a]는 지지부 A에서 고정되고 B에서 단순 지지되고 있다; 이러한 보를 일단고정 타단지지 보(propped cantilever beam or fixed simple beam)라 부른다. 보의 반력들은 A에서의 수직 및 수평력, 우력 그리고 B에서의 수직력이다. 정적 평형에 의한 독립적인 방정식이 3개 밖에 없으므로 이들 4개의 반력들을 정적으로 구하는 것은 불가능하다. 평형 방정식을 초과하는 반력의 수를 정적 부정도(degree of statical indeterminacy)라 한다. 따라서 그림 [a]의 보는 1도의 정적 부정도를 가진다. 정적으로 결정될 수 있는 지지구조를 초과하는 반력들을 정적 잉여(statical redundants)라고 부르며, 이러한 잉여의 수는 정적 부정도와 같다. 예를 들어 그림 [a]의 반력 Rb는 잉여 반력이라 할 수 있다. 지지부 B가 제거되면 외팔보가 되는 것에 주목한다. 이러한 잉여가 제거된 정정(statically determinate) 구조를 제거구조(released structure) 또는 기본구조(primary structure)라 한다.

그림 [a] 보의 다른 접근법은 반력 모멘트 Ma를 잉여로 생각하는 것이다; 이 모멘트가 제거되면, 제거구조는 부동힌지지점(pin support) A와 가동힌지지점(roller support) B를 가진 단순보가 된다.

양단고정보(fixed ens beam or fixed-fixed beam or clamped beam)가 그림 [b]에 나타나 있다. 각 지지부에 3개의 반력 성분들을 가지고 있다; 따라서 보는 전부 미지의 반력 6개를 가지고 있다. 3개의 평형 방정식이 있으므로, 3도의 부정정 보가 된다. 일단에서 3개의 반력을 잉여로 취하고 제거하면, 외팔보가 제거구조로 남게 된다. 만약 고정단에서 2개의 모멘트와 1개의 수평 반력을 제거하면, 제거구조는 단순보가 된다.

윗 그림의 나머지 2개의 보들은 1개 이상의 너비를 가지고 연속적으로 지점에 걸쳐 있어 연속보(continuous beams)라 불리우는 것들이다. 그림 [c]는 4개의 반력과 3개의 정적 평형 방정식을 가지므로 1도의 부정정 보이다. Rb를 잉여로 취하고 지점 B를 제거하면, 정정 단순보 AC가 된다. 만약 Rc가 잉여로 선택되면 제거구조는 돌출부 BC를 가진 단순보 AB가 될 것이다.

윗 그림의 마지막 보의 부정정도는 2도이다. Rb와 Rc를 잉여로 선택하면 제거구조는 외팔보가 된다.