구간, ε-근방

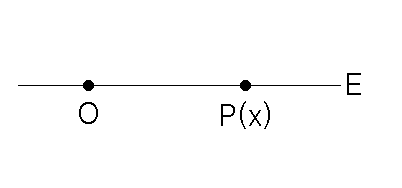
실수 전체 집합 R의 원과 직선 상의 점 전체 집합 L 간에는 일대일 대응이 성립한다. 이 때 L의 점 P의 좌표가 x 이면 P(x)로 나타낸다.

실수 a, b에 의하여 정해진 집합을 구간(區間)이라고 한다.

\[\begin{split}(a,\,b)&=\left\{x\in{\bf R}|a<x<b\right\}\\\left[a,\,b\right)&=\left\{x\in{\bf R}|a\le x<b\right\}\\\left(a,\,b\right]&=\left\{x\in{\bf R}|a<x\le b\right\}\\\left[a,\,b\right]&=\left\{x\in{\bf R}|a\le x\le b\right\}\end{split}\]

(a, b)를 개구간(開區間), [a, b), (a, b]를 반개구간(半開區間), [a, b]를 폐구간(閉區間)이라 한다. b-a는 그 구간의 나비이다. 이들은 유한구간(有限區間)이라고도 한다.

다음 각 조건을 만족하는 x로 이루어지는 집합을 생각해 본다.

\[x>a,\quad x\ge a,\quad x<a,\quad x\le a\]

이들을 각각 다음과 같이 표시한다.

\[(a,\,\infty),\quad[a,\,\infty),\quad(-\infty,\,a),\quad(-\infty,\,a]\]

이들은 무한구간(無限區間)이라 한다.

같은 방법으로 실수 전체 집합 R을 (-∞, ∞)로 나타낸다.

점 a에서의 거리가 ε(>0) 보다 작은 점들의 집합

|x-a|<ε

를 만족하는 x의 집합, 개구간 (a-ε, a+ε)을 점 a의 'ε-근방'이라 하고 다음과 같이 표기한다.

\[{\rm N}_\epsilon(a)=\left\{x\in{\bf R}|a-\epsilon<x<a+\epsilon\right\}\]

《문      제》

1. 다음 구간에 속하는 x의 조건을 부등식으로 나타내라.
(1) [0, 1],   (0, 1],   [0, 1),   (0, 1)
(2) [0, ∞),   (0, ∞)             (3) (-∞, -1],   (-∞, 10)
<풀이>
(1) 0≤x≤1,   0<x≤1,   0≤x<1,   0<x<1
(2) x≥0,   x>0       (3) x≤-1,   x<10

2. 다음 부등식을 구간으로 나타내라.
(1) -1<x<1   (2) 0≤x<5   (3) -1/2≤x≤3/5   (4) 0<x≤9   (5) |x|<1   (6) |x|≤2
<풀이>
(1) (-1, 1)   (2) [0, 5)   (3) [-1/2, 3/5]   (4) (0, 9]   (5) (-1, 1)   (6) [-2, 2]

3. 다음 부등식을 만족하는 실수 x의 집합을 구간으로 나타내라.

\((1)\ x^2-3x-4\le0\qquad(2)\ 2\le|x|<3\)

<풀이>

(1) (x-4)(x+1)≤0, [-1, 4]     (2) (-3, -2]∪[2, 3)

4. 문제 3에서 (1)의 집합을 A, (2)의 집합을 B라고 할 때 다음을 구간으로 나타내라.

(1) A∪B                    (2) A∩B

<풀이>

(1) (-3, -2]∪[-1, 4]         (2) [2, 3)