도심 (Centroids of Areas)

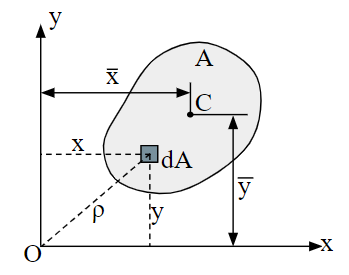
 평면 상 면적의 도심(centroid) 위치는 단면의 중요한 기하학적 성질이다. 도심의 좌표를 정의하기 위해, 그림 1과 같이 면적 A와 xy 좌표계를 생각한다.

그림 1 면적 A의 도심 C

x와 y축에 대한 면적의 1차 모멘트(first moments)는 각각 다음과 같다.

\[Q_x=\int ydA\qquad Q_y=\int xdA\]

도심 C(그림 1)의 x 및 y의 좌표는 1차 모멘트를 그의 면적으로 나눈 것과 같다.

\[\overline x={Q_y\over A}=\frac{\int xdA}{\int dA}\qquad\overline y={Q_x\over A}=\frac{\int ydA}{\int dA}\]

만약 이 면적의 경계가 단순한 수학적 표현으로 정의된다면, 윗 식과 같이 닫힌 형태의 적분으로 계산할 수 있으며 x와 y에 대한 식을 얻을 수 있다.

그림 2 단축 대칭 / 양축 대칭 / 점대칭 단면

단면이 축에 대해서 대칭(symmetric about an axis)이면, 1차 모멘트는 대칭축에 대하여 영이므로 도심은 대칭축 상에 있어야 한다. 예를 들면 그림 2의 왼쪽과 같이 단축대칭 단면의 도심은 대칭축인 x축 상에 놓여야 한다. 그러므로 도심을 결정하기 위해서는 하나의 거리만 계산하면 된다. 단면이 그림 2의 중앙과 같이 두개의 대칭축을 가질 경우, 도심의 위치는 대칭축 간의 교점이므로 관찰에 의해 결정할 수 있다. 그림 2의 오른쪽은 점대칭(symmetric about point) 단면이다. 이 경우 대칭축은 없지만, 단면 상에서 어느 점을 지나는 모든 선들이 그 점에 대하여 대칭인 점(소위 대칭 중심(center of symmetry))이 존재한다, 당연히 도심은 대칭 중심과 일치하므로 관찰에 의해 결정될 수 있다.

단면 경계가 수학적으로 표현될 수 없는 비정형일 경우, 윗 식의 적분을 근사 수치해석으로 구한다. 가장 단순한 방법으로 면적을 미소요소 \(\Delta A_i\)로 나누고 적분을 총합으로 계산한다.

\[A=\sum_{i=1}^n\Delta A_i\qquad Q_x=\sum_{i=1}^ny_i\Delta A_i\qquad Q_y=\sum_{i=1}^n x_i\Delta A_i\]

여기서 n은 면적요소의 전체 개수, \(y_i\)는 면적 \(\Delta A_i\) 도심의 y좌표, 그리고 \(x_i\)는 면적 \(\Delta A_i\) 도심의 x좌표이다. 이 도심에 대한 계산의 정확도는 선택 요소들이 실제 면적에 얼마나 적합한가에 달려 있다.

[예제]  반분할된 포물선 단면이 x축, y축 및 포물선(parabolic curve)과 경계를 이루고 있다(그림 3). 곡선의 방정식에서 b는 밑변이고 h는 높이이다. 이 반분할 단면의 도심 C의 위치를 결정하라.

그림 3 반분할 포물선

<풀이>  분석을 위해, 그림과 같이 폭 dx와 높이  y의 면적요소 dA를 취하면 전체 단면의 면적은

\[\int dA=\int ydx=\int_0^bh\left(1-{x^2\over b^2}\right)dx={2bh\over3}\]

이다. 임의의 축에 대한 면적요소의 1차 모멘트는 그 축으로부터 도심까지 거리와 요소의 면적을 곱하면 된다. 요소 도심의 x와 y 좌표는 각각 x와 y/2 이므로, 1차 모멘트는 다음과 같다.

\[\begin{split}&Q_x=\int{y\over2}dA=\int_0^b{h^2\over2}\left(1-{x^2\over b^2}\right)^2dx={4bh^2\over15}\\&Q_y=\int xdA=\int_0^bhx\left(1-{x^2\over b^2}\right)dx={b^2h\over4}\end{split}\]

이제 도심 C의 좌표를 다음과 같이 결정할 수 있다.

\[\overline x={Q_y\over A}={3b\over8}\qquad\overline y={Q_x\over A}={2h\over5}\]