Kriging
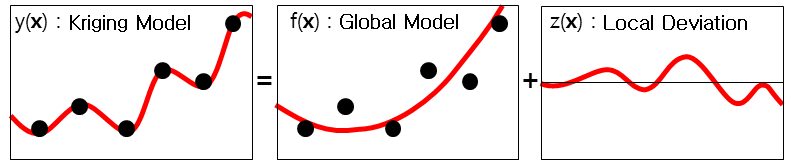
Kriging started when Metheron mathematically established the empirical research of South African mining scientist Krige. The Kriging meta model consists of the sum of the global model f(x) and the local deviation z(x).
\[y(\overrightarrow{x})=f(\overrightarrow{x})+z(\overrightarrow{x})=\sum_{i=1}^k\beta_if_i(\overrightarrow{x})+z(\overrightarrow{x})\]
In the above equation, f(x) is a polynomial function, \(\beta_i\) is a regression constant vector, z(x) is a Gaussian process of a normal distribution with mean 0 and variance \(\sigma^2\), and y(x) represents the residual of the mean. In this case, the covariance in each design variable vector \({\bf x},{\bf x}'\) is as follows.
\[Cov[z(\overrightarrow{x}),z(\overrightarrow{x}')]=\sigma^2R(\overrightarrow{x},\overrightarrow{x}')=\sigma^2R(\overrightarrow{d}),\ \text{where}\ \overrightarrow{d}=\overrightarrow{x}-\overrightarrow{x}'\]
Where R is the correlation function.
The influence of the shape of the global model and the variables of the correlation function on the accuracy of the Kriging model is not large. The correlation function is as follows.
\[R(\overrightarrow{d})=\prod_{i=1}^{ndv}\exp(-\theta_i|d_i|^{p_i})=\exp(-\sum_{i=1}^{ndv}\theta_i|d_i|^{p_i})\]
The value of the required variables of the correlation function are obtained using the global optimization of MLE, maximum likelihood estimation(nexp: number of experiment, ndv: number of variable).
s.t. \(\theta_i\ge0,\ 0\le p_i\le2,\ i=1,\ \cdots,\ ndv\)
The advantage is that it expresses well even if the nonlinearity is severe and is not sensitive to user-specified values. The disadvantage is that it is difficult to generate because the global optimization needs to be solved, and if the number of experiment points increases, the correlation matrix becomes numerically unstable.
Source : https://www.pidotech.com



댓글
댓글 쓰기