기계공학 (Mechanical Engineering)

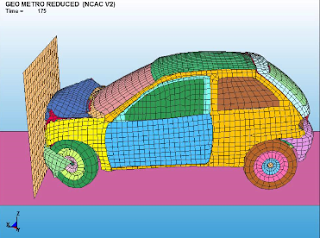
메타모델(metamodel)이란 실제모델을 대체할 수 있는 근사모델을 말한다. 실제 해석모델은 반응값을 구하기 위해 실제 시험보다 저렴하나 많은 함수 호출(function call)이 필요한 최적설계(optimization)에 있어서 시간/비용이 많이 든다고 볼 수 있다. 최소의 해석회수로 메타모델을 생성하면 이러한 부담없이 최적해 도출이 가능하다. 실제모델 메타모델 ● 1회 해석 시 시간/비용이 많이 소요된다. ● 설계영역 탐색에 많은 회수의 해석을 요하는     최적설계에 적용이 어렵다. ● 특성치 계산에 수치적 부담이 없다. ● 많은 수의 함수 호출이 필요한     설계영역의 탐색, 최적설계에 적합하다. - 실험계획법을 이용한 메타모델 생성 및 활용   (1) 실험점 배치 및 시험 또는 해석 실시(Locate sample points and perform analysis)   (2) 메타모델 생성 및 선정(Build metamodels and select the most accurate one)   (3) 최적해 예측 및 신뢰성 평가(Prediction design optimization and uncertainty       assessment) - 데이터 이용 메타모델 생성 및 활용   (1) 시험/해석/경험(Experiments/CAE/Experience)→데이터(Data)→전처리:데이터 누락/       이상점...(Pre-processing:Missing data/Outlier...)   (2) 메타모델 생성(Metamodel Generation)   (3) 성능예측/최적설계/신뢰성 평가(Prediction/Design Optimization/Uncertainty        Assessment) - 이상점(Outlier) 검출   이상점이 있는 경우 메터모델 성능이 저하되므로 제거되어야 한다.   발생 원인 : 해석/시험 상 오류, 데이터 작성 오류 - 메타모델의 종류 회귀 모델

So No problem. What time shall we meet? 문제없어요. 몇 시에 만날까요? Sophie! What are you doing after work tonight? 소피! 오늘 저녁에 퇴근하고 뭐해? Sounds like fun! 재미있겠네! So you'd like me to come with you and give it the once-over? 그러니까 같이 가서 좀 봐달라는 거였군요?

But you know I don't know anything about car. (근데 아시잖아요. 저 차에 대해서 잘 모르는 거.)

Of course. Can you please spell your name for me? 물론이죠. 성함 스펠링을 알려주실 수 있으신지요? Of course. You only have to ask. 물론이죠 말만 하세요. Oh, I see. So, what brings you here? 아 그렇군요. 무슨 일로 오셨나요? Oh, this is Jane from Donman Company. Can you ask her to call me back? 돈만사의 제인입니다. 저한테 전화 다시 해달라고 전해주시겠어요?

Could you do me a favor? (부탁 하나 들어주시겠어요?)

아래 그림과 같이 끝단에 우력 T가 작용하여 비틀림을 받는 원형단면의 축(bar of shaft)을 생각한다. 이와 같이 하중을 받는 축은 순수 비틀림(pure torsion) 상태로 불리운다. 대칭성으로부터 원축의 단면은 종축을 중심으로, 반경이 직선을 유지하고, 단면은 평면과 원형을 유지하는 강체회전(rigid body rotation)을 한다고 볼 수 있다. 또한, 축의 전체의 비틀림 각도가 미소하다면, 축의 길이와 반경은 변하지 않을 것이다. 그림 1 원축의 순수 비틀림 만약 축의 좌단이 고정이면, 우단은 미소각도 Φ 만큼 좌단에 대해서 회전할 것이다(위의 그림1a). 각도  Φ는 비틀림 각(angle of twist) 으로 알려져 있다. 더우기 표면의 종방향 직선도 미소각도 만큼 회전할 것이다. 이러한 회전 때문에, 그림의 길이가 dx인 직사각형 미소요소는 정사방형 형태로 변형하게 된다(그림 1b). 이 요소 양변의 길이는 변하지 않으나 모서리 각도는 더이상 90˚가 아니다, 따라서 이 요소는 순수전단 (pure shear) 상태에 있고 전단변형률 의 크기 γ는 모서리 직각으로부터 감소한 각도와 같다. 각도의 감소는 반경 r의 단면이 다른면에 대해서 rd Φ 만큼 회전한 것이므로 전단변형률은 다음과 같다. \[\gamma=\frac{rd\phi}{dx}=r\theta={r\phi\over L}\] 여기서 d Φ/dx는 비틀림 각  Φ의 변화율을 나타낸다. 일반적으로,  Φ와 d Φ/dx 모두 x의 함수이다.  d Φ/dx를 기호 θ로 표시하고 단위길이 당 비틀림 각(angle of twist per unit length) 이라 한다. 순수 비틀림은 특별한 경우로 모든 딘면들이 동일한 토오크를 받으므로, d Φ/dx를 축의 길이에 걸쳐서 상수로 할 수 있다. 따라서 θ= Φ/L을 얻으며, L은 축의 길이이다. 이상의 방정식들은 기하학적 개념에 근거한 것이므로, 탄성, 또는 비탄성, 선형 또는 비선형에 상관없이 어떤 재질의 원축에도 유효하다.

이전 글 에서는 쌍곡선/삼각함수를 이용하여 3차 방정식의 근의 공식을 유도하였다. 이번에는 카르다노의 해법을 통하여 근을 구해본다. 3차 방정식의 일반식(1)을 이전 글과 동일하게 계수 p, q로 치환한다.(2). 유도 과정은 이전 글을 참조한다. \(z^3+a_2z^2+a_1z+a_0=0\cdots(1)\) \(\begin{align}z=x-{a_2\over3},\ p={3a_1-a_2^2\over3},\ q={9a_1a_2-27a_0-2a_2^3\over27},\ x^3+px=q\cdots(2)\end{align}\) 방정식 (2)를 풀기위해 x를 다음과 같이 변수 t로 식 (3)과 같이 치환한 후 t³을 곱하면 t³에 대한 2차 방정식을 얻는다.(4) \(x=t-\dfrac{p}{3t}\cdots(3)\) \((t^3)^2-q(t^3)-\dfrac{p^3}{27}=0\cdots(4)\) 2차 방정식의 근의 공식으로부터 \(t^3=\dfrac{q}{2}\pm\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}={\rm R}\pm\sqrt{{\rm R}^2+{\rm Q}^3}\cdots(5)\) 여기서 R=q/2, Q=p/3으로 간략화 했다. 식 (5)는 3차 방정식이므로 각 +/- 부호에 따라 3개의 근을 갖는다.(6) 허근 ω 에 대하여는 링크를 참조한다. \(t=\begin{cases}{\rm A},\ \omega{\rm A},\ \omega^2{\rm A}\\{\rm B},\ \omega{\rm B},\ \omega^2{\rm B}\end{cases}\cdots(6)\) 여기서 \(\begin{align}\omega=-{1\over2}+{\sqrt{3}\over2}i,\ {\rm A}=\sqrt[3]{{\rm R}+\sqrt{{\rm R}^2+{\rm Q}^3}},\ {\rm B}=\sqrt[3]{{\rm R}-\sqrt{{\rm R}^2+{\rm Q}^3}}\cdots(7)\end{a

소개 (Introduction) 연속방정식이 질량 보존에 관한 것이라면 나비어-스톡스 방정식은 운동량에 관한 것이다. 유체역학의 지배방정식으로 유명하며 통상 그 규모와 복잡성으로 난해한 것으로 여겨진다. 본 글에서는 연속방정식, 평형방정식 , 전미분  및 변형률 속도텐서 를 활용한 유도과정을 소개한다. 나비어-스톡스 방정식 (Navier-Stokes Equation) 유도과정을 평형방정식에서 출발한다. 가속도항을 전미분으로 나타내면 \[\nabla\cdot\boldsymbol\sigma+\rho{\bf f}=\rho{\bf a}=\rho\left(\frac{\partial{\bf v}}{\partial t}+{\bf v}\cdot\nabla{\bf v}\right)\] 응력 을 정수압(-p)과 편향응력( σ ') 으로 분해하면 \[\boldsymbol\sigma=-p{\bf I}+\boldsymbol\sigma'\] 이 식을 평형방정식에 대입한다. \[\nabla p+\nabla\cdot\boldsymbol\sigma'+\rho{\bf f}=\rho\left(\frac{\partial{\bf v}}{\partial t}+{\bf v}\cdot\nabla{\bf v}\right)\] 이제부터는 점성 유체유동의 구성모델(constitutive model)을 적용한다. 이 구성모델은 전단변형률 속도와 편향응력과의 관계를 정의한다. \[\boldsymbol\sigma'=2\mu{\bf D}'\] 여기서 μ는 유체의 점성계수 이다. 사실 위의 식은 \(\tau=\mu(\partial v_x/\partial y)\)의 3-D 형태이다. 이 식을 대입하고 μ를 상수로 가정하면 가장 일반화된 형태의 방정식을 얻는다. \[\rho\left(\frac{\partial{\bf v}}{\partial t}+{\bf v}\cdot\nabla{\bf v}\right)=-\nabla p+2\mu\cdot{\bf D}'+\rho{\bf f