원축의 비틀림 (Torsion of Circular Bars)
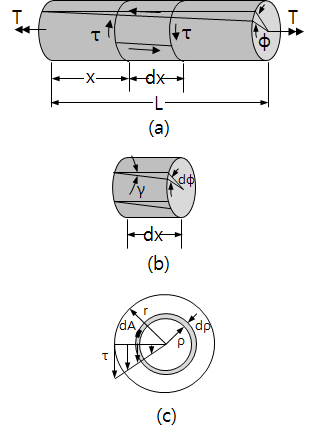 |
| 그림 1 원축의 순수 비틀림 |
\[\gamma=\frac{rd\phi}{dx}=r\theta={r\phi\over L}\]
여기서 dΦ/dx는 비틀림 각 Φ의 변화율을 나타낸다. 일반적으로, Φ와 dΦ/dx 모두 x의 함수이다. dΦ/dx를 기호 θ로 표시하고 단위길이 당 비틀림 각(angle of twist per unit length)이라 한다. 순수 비틀림은 특별한 경우로 모든 딘면들이 동일한 토오크를 받으므로, dΦ/dx를 축의 길이에 걸쳐서 상수로 할 수 있다. 따라서 θ=Φ/L을 얻으며, L은 축의 길이이다. 이상의 방정식들은 기하학적 개념에 근거한 것이므로, 탄성, 또는 비탄성, 선형 또는 비선형에 상관없이 어떤 재질의 원축에도 유효하다.
원축의 전단응력 τ는 그림 1a에서 보는 바와 같은 방향을 가지고 있다. 선형탄성 재료(linear elastic material)에 대해서는, 전단상태의 응력과 변형률의 관계가 후크의 법칙(Hooke's law)를 따르므로 다음식을 얻는다.
\[\tau=G\gamma=Gr\theta\]
여기서 G는 세로탄성계수(shear modulus of elasticity)이다. 위의 식들은 단위길이당 비틀림 각과 축 표면의 응력과 변형률의 관계를 나타낸다.
축 내부의 변형률과 응력은 표면요소의 그것들과 유사한 방법으로 결정된다. 왜냐하면 비틀림을 받는 동안 단면의 반경들이 직선을 유지하고 찌그러지지 않기 때문에, 반경 ρ의 원통면에 위치한 요소에도 동일하게 적용할 수 있다(그림 1c). 따라서 이러한 내부요소 또한 순수전단 상태이며, 해당 전단변형률과 전단응력은 다음식으로 주어진다.
\[\gamma=\rho\theta\qquad\tau=G\gamma=G\rho\theta\]
이들 식은 원축의 전단변형률 및 응력이 중심에서의 반경방향 거리 ρ에 따라 선형적으로 변화함을 보여주며, 최대값은 최외각면 요소에서 발생한다. 단면의 응력 분포는 그림 1c와 같이 삼각형 선도를 나타낸다.
단면에 작용하는 전단응력은 동일 크기의 종단면에 작용하는 전단응력을 수반한다(그림 2). 이 결과는 동일 전단응력이 상호 수직한 면에 항상 존재한다는 사실에 따른 것이다. 만약 나무와 같이 횡단면보다 종단면이 전단에 취약한 재질은 비틀림에 의한 첫번째 크랙이 표면에 종방향으로 발생한다.
 |
| 그림 2 원축의 종방향 전단응력 |
 |
| 그림 3 축방향 45˚ 요소에 작용하는 인장 및 압축응력 |
작용 토오크 T와 비틀림 각 Φ의 관계(그림 1a)는 단면에 걸쳐 작용하는 전단응력(그림 1c)의 합력(resultant)이 토오크 T와 정적 평형을 이룬다는 조건으로부터 결정된다. 요소 dA에 작용하는 전단력은 τdA 이고, 이 힘의 중심에 대한 모멘트는 \(\tau\rho dA=G\theta\rho^2dA\) 이다. 전체 토오크 T는 단면적에 작용하는 이러한 요소 모멘트들의 합이다. 따라서,
\[T=\int G\theta\rho^2dA=G\theta\int\rho^2dA=G\theta I_p\]
여기서 Ip는 원형단면의 극관성모멘트(polar moment of inertia)이다. 반경 r 이고 직경 d인 원의 극관성모멘트는 다음과 같다.
\[I_p={\pi r^4\over2}={\pi d^4\over32}\]
다음은 앞의 식으로부터
\[\theta={T\over GI_p}\]
여기서 단위길이당 비틀림 각 θ는 토오크 T에 비례하며, 축의 비틀림 강도(torsional rigidity)로 알려진 GIp에 반비례한다. 전체 비틀림 각 Φ는 θL과 같으므로
\[\phi=\theta L={TL\over GI_p}\]
GIp/L의 양은 원축의 비틀림 강성(torsional stiffness)으로 단위각도를 회전시키는데 필요한 토오크를 나타낸다. 또한 비틀림 연성(torsional flexibility)은 강성의 역수로서 L/GIp이며 단위 토오크가 발생시키는 각도이다.
위의 식은 여러가지 재질의 세로탄성계수 G를 결정하는데 사용된다. 원형 시편의 비틀림 시험을 통하여 알고 있는 토오크 T에 대하여 각도 Φ를 정할 수 있다. 그러면 G 값은 윗식을 통하여 계산된다.
비틀림을 받는 원축의 최대전단응력(maximum shear stress) \(\tau_{\rm max}\)는 τ에 관한 식에 θ에 관한 식을 대입하면 구할 수 있다.
\[\tau_{\rm max}=Gr\theta={Tr\over I_p}={16T\over\pi d^3}\]
이 방정식은 비틀림 공식(torsion formula)로 알려져 있고, 최대전단응력은 토오크 T와 반경 r에 비례하고 단면의 극관성 모멘트에 반비례한다. 중심에서 거리 ρ의 전단응력은 다음과 같이 구할 수 있다.
\[\tau=G\rho\theta={T\rho\over I_p}\]
중공 원축 (Hollow circular bars)
중공축(hollow shaft)은 중실축(solid shaft)에 비해 비틀림 하중을 견디는데 휠씬 효율적이다. 언급한 바와 같이 중실축에서 전단응력은 단면의 최외각 경계에서 최대이고, 중심에서 영이 된다. 그러므로, 중실축의 대부분 재료는 허용 전단응력 이하의 응력을 받게 된다. 중량절감이 중요시 된다면, 중실축의 사용이 바람직하다.
중공축의 비틀림 해석은 중실축의 그것과 거의 동일하다. 따라서, 전단변형률 γ와 전단응력 τ에 관한 기본공식들을 그대로 사용할 수 있다.
 |
| 그림 4 중공원축 |
\[I_p=\int_{r_1}^{r_2}\rho^2dA={\pi\over2}(r_2^4-r_1^4)={\pi\over32}(d_2^4-d_1^4)\]
박육 중공관의 경우, 아래 근사식을 사용할 수 있다.
\[I_p\approx2\pi r^3t={\pi d^3t\over4}\]
여기서 r과 d는 각각 평균반경과 직경이다. 중실축에서 유도된 θ, Φ 및 τ에 관한 공식들은, Ip가 위의 식들로 계산된다면, 중공축에도 사용할 수 있다. 물론, 중공축의 벽두께는 주름과 좌굴을 회피할 정도로 충분하여야 한다.
[예제 1] 직경이 60mm 인 중실 강재축이 허용 전단응력 \(\tau_{\rm allow}=40\)MPa 및 단위길이 당 허용 비틀림 각 θ=1˚/m로 설계되어 있다. 축의 최대 허용 토오크 T를 결정하여라. 단, G=80GPa 이다.
<풀이> 허용 전단응력을 기준으로 한 허용 토오크 \(T_1\)은 비틀림 공식에 의하여 구할 수 있다.
\[T_1={\pi d^3\tau_{\rm allow}\over16}={\pi(0.06)^3(40\times10^6)\over16}=1,695\ {\rm N\cdot m}\]
단위길이 당 허용 비틀림 각을 기준으로 한 허용 토오크 \(T_2\)는 앞의 공식으로 다음과 같이 구한다.
\[T_2=GI_p\theta=(80\times10^9)\left({\pi\over32}\right)(0.06)^4\left(\pi\over180\right)=1,780\ {\rm N\cdot m}\]
이들 두개의 값 중에서 작은 값이 최대 허용 토오크이므로 T=1,695 N·m 이다.
[예제 2] 동일 재료로 제작된 중공축과 중실축이 동일 길이, 동일 외측반경 r를 가지고 있다(그림 5). 중공축의 내측반경은 0.6r 이다 두 축 모두 동일 토오크를 받는다고 하면 축에 발생하는 최대 전단응력을 비교하여라. 또한, 두 축의 중량과 회전각을 비교하여라.
 |
| 그림 5 예제 2 |
\[I_p={\pi r^4\over2}=0.5\pi r^4\]
그리고 중공축에 대해서는
\[I_p={\pi r^4\over2}-{\pi(0.6r)^4\over2}=0.4352\pi r^4\]
따라서, 중실축에 대한 중공축의 최대 전단응력의 비율은 0.5/0.4352=1.15 이다. 회전각도 응력과 동일 비율을 가진다.
축의 중량은 단면적에 비례하므로, 중실축의 중량은 \(\pi r^2\)에 비례하고 중공축은 \(\pi r^2-\pi(0.6r)^2=0.64\pi r^2\)에 비례한다. 그러므로, 중공축의 중량은 중실축의 64% 이다. 이 예제에서 중공축의 응력과 회전각은 15% 더 크지만 36%의 중량이 절감된다.



댓글
댓글 쓰기