[연습문제] 함수
<풀이>
\((1)\ 1+x\ne0\ 이어야\ 하므로\ D_f=\{x\in R|x\ne-1\},\,\lim_{x\to\pm\infty}f(x)=0\ 이므로\\\quad\ \ R_f=\{y\in R|y\ne0\}\\(2)\ D_f=(-\infty,\infty),\,x^2\ge0\ 이므로\ R_f=(0,1]\\(3)\ D_f=[0,\infty),\,\lim_{x\to\infty}f(x)=0\ 이므로\ R_f=(0,1]\\(4)\ D_f=(-\infty,\infty),\,f(x)=(x-2)(x-1)에서\ 최소값\ f({3\over2})=-{1\over4}\ 이므로\ R_f=[-{1\over4},\infty)\\(5)\ (x-3)(x+1)\ge0\ 이므로\ D_f=(-\infty,-1]\cup[3,\infty),\,R_f=[0,\infty)\\(6)\ x(x-1)(x-2)\ge0\ 이므로\ D_f=[0,1]\cup[2,\infty),\,R_f=[0,\infty)\\(7)\ x+2\ne0\ 이므로\ D_f=\{x\in R|x\ne-2\},\,f(x)=2-{1\over x+2}\ne2\ 따라서\\\quad \ R_f=\{y\in R|y\ne2\}\)
2. 실수 a, b에 대하여 작지 않은 것은 max{a, b}, 크지 않은 것은 min{a, b}라 할 때 다음이 성립함을 보여라.
\[\max\{a,b\}=\frac{a+b+|a-b|}{2},\,\min\{a,b\}=\frac{a+b-|a-b|}{2}\]
<풀이>
\(a\ge b\ 일\ 때\ |a-b|\ge0\ 이므로\ \max\{a,b\}={a+b+a-b\over2}=a,\,\min\{a,b\}={a+b-a+b\over2}=b\\a<b\ 일\ 때\ |a-b|<0\ 이므로\ \max\{a,b\}={a+b-a+b\over2}=b,\,\min\{a,b\}={a+b+a-b\over2}=a\)
3. 다음 함수 중에서 우함수ㆍ기함수ㆍ주기함수를 각각 찾아 내어라.
\((1)\ y=2x\quad(2)\ y=x^2-4\quad(3)\ y=x-x^3\quad(4)\ y=\cos2x\quad(5)\ y=\sin{x}+\cos{x}\\(6)\ y=\sin{x}+\tan{x}\quad(7)\ y={\sin{x}\over x}\quad(8)\ y={x\over1+x^2}\)
<풀이>
\((1)\ f(-x)=-2(-x)=2x=-f(x)\ :\ 기함수\\(2)\ f(-x)=(-x)^2-4=x^2-4=f(x)\ :\ 우함수\\(3)\ f(-x)=(-x)=(-x)-(-x)^3=-x+x^3=-f(x)\ :\ 기함수\\(4)\ f(-x)=\cos2(-x)=\cos2x=f(x)\ :\ 우함수\\\quad\ \ f(x+\pi)=\cos2(x+\pi)=\cos(2x+2\pi)=\cos2x=f(x)\ :\ 주기함수\\(5)\ f(-x)=\sin(-x)+\cos(-x)=-\sin{x}+\cos{x}\ne f(x)\ne-f(x)\\\quad\ \ f(x+2\pi)=\sin(x+2\pi)+\cos(x+2\pi)=\sin{x}+\cos{x}=f(x)\ :\ 주기함수\\(6)\ f(-x)=\sin(-x)+\tan(-x)=-(\sin{x}+\tan{x})=-f(x)\ :\ 기함수\\\quad\ \ f(x+2\pi)=\sin(x+2\pi)+\tan(x+2\pi)=\sin{x}+\tan{x}=f(x)\ :\ 주기함수\\(7)\ f(-x)={\sin(-x)\over-x}={\sin{x}\over x}=f(x)\ :\ 우함수\\(8)\ f(-x)={-x\over1+(-x)^2}=-f(x)\ :\ 기함수\)
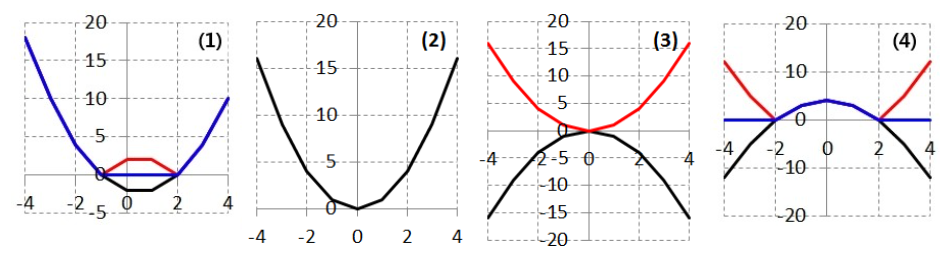
4. 다음식으로 정의된 함수 f에 대하여
\[y=f(x),\quad\color{red}{y=|f(x)|},\quad\color{blue}{y={1\over2}\{f(x)+|f(x)|\}}\]
의 그래프를 그려라.
\[\begin{align}&(1)\ f(x)=(x-2)(x+1)\qquad(2)\ f(x)=x^2\\&(3)\ f(x)=-x^2\qquad\qquad\qquad\ \,(4)\ f(x)=4-x^2\end{align}\]
<풀이>
5. f(x)=ax+b, g(x)=cx+d 라 할 때 항상
\[(f\circ g)(x)=(g\circ f)(x)\]
이기 위한 필요충분조건을 a, b, c, d로 나타내어라.
<풀이>
\((f\circ g)(x)=f(g(x))=a\{g(x)\}+b=a(cx+d)+b=acx+ad+b\\(g\circ f)(x)=g(f(x))=c\{f(x)\}+d=c(ax+b)+d=acx+bc+d\\\therefore\ ad+b=bc+d\)
6. \(f(x)=\frac{ax+b}{cx+d}\)에서 d=-a 이면 \(f\circ f\)가 항등함수, 곧 f(f(x))=x 임을 보여라. 단, a²+bc≠0.
<풀이>
\(\begin{align}(f\circ f)(x)&=f(f(x))=\frac{a\{f(x)\}+b}{c\{f(x)\}+d}=\frac{a\left(\frac{ax+b}{cx+d}\right)+b}{c\left(\frac{ax+b}{cx+d}\right)+d}=\frac{a^2x+ab+bcx+bd}{acx+bc+cdx+d^2}\\&=\frac{a^2x+ab+bcx-ab}{acx+bc-acx+a^2}=\frac{x(a^2+bc)}{a^2+bc}=x\end{align}\)
7. \(f(x)={x\over x-1}\) 일 때
\((1)\ f({1\over x})\qquad(2)\ f(-x)\qquad(3)\ (f\circ f)(x)\qquad(4)\ f\left({1\over f(x)}\right)\)
을 구하여라.
<풀이>
\(\begin{split}&(1)\ f\left({1\over x}\right)=\frac{\left(1\over x\right)}{\left(1\over x\right)-1}={1\over1-x}\qquad(2)\ f(-x)=\frac{(-x)}{(-x)-1}={x\over x+1}\\&(3)\ (f\circ f)(x)=f(f(x))=\frac{f(x)}{f(x)-1}=\frac{\left(x\over x-1\right)}{\left(x\over x-1\right)-1}=x\ (항등함수)\\&(4)\ f\left(1\over f(x)\right)=f\left(x-1\over x\right)=\frac{\left(x-1\over x\right)}{\left(x-1\over x\right)-1}=1-x\end{split}\)
8. x의 음함수 y가 xy²+2x+3y²=1로 주어져 있다. 이것에서 음함수의 분지를 구하여라.
<풀이>
\(y^2=\frac{1-2x}{x+3}에서\ y=f(x)=\sqrt{\frac{1-2x}{x+3}}(y\ge0),\,y=g(x)=-\sqrt{\frac{1-2x}{x+3}}(y<0),\,\frac{1-2x}{x+3}\ge0\ 이므로\\정의역\ D_f=(-3,{1\over2}]\)
9. \(x={t\over1+t^2},\,y=1+t^2,\,-\infty<t<\infty\) 일 때 x, y의 관계식을 구하고, x와 y의 범위를 각각 구하여라.
<풀이>
\(x^2=\frac{t^2}{(1+t^2)^2}={y-1\over y^2},\,x^2y^2-y+1-0,\,{dx\over dt}=\frac{1-t^2}{(1+t^2)^2}=0\ 에서\ t=\pm1\ 일\ 때\ 극치\ x=\pm{1\over2}\\이므로\ -{1\over2}\le x\le{1\over2},\,t^2\ge0\ 이므로\ y\ge1\)
10. \(\tan{\theta\over2}=t\) 라 할 때 \(\cos\theta=\frac{1-t^2}{1+t^2},\,\sin\theta=\frac{2t}{1+t^2}\) 임을 증명하여라.
<풀이> 삼각함수 항등식을 활용한다.
\(\frac{1-t^2}{1+t^2}=\frac{1-\tan^2{\theta\over2}}{1+\tan^2{\theta\over2}}=\cos^2{\theta\over2}-\sin^2{\theta\over2}=\cos\theta\\\frac{2t}{1+t^2}=\frac{2\tan{\theta\over2}}{1+\tan^2{\theta\over2}}=2\sin{\theta\over2}\cos{\theta\over2}=\sin\theta\)



댓글
댓글 쓰기