엑셀을 사용하여 회귀분석하기

엑셀을 활용하면 다중 선형 회귀분석을 쉽게 할 수 있다. 예제를 통하여 알아 본다.

[예제] KBL(한국농구리그)의 선수 신체조건과 평균 리바운드 개수가 다음과 같을 때 만약 신장 216 cm, 체중 151 kg, 윙스팬 229 cm인 샤킬오닐이 KBL에서 뛸 경우 다중 선형 회귀분석으로 리바운드 개수를 추정하라. 

아래와 같이 독립변수와 종속변수를 정의한다.

y : 리바운드(개/경기), x1 : 신장(cm), x2 : 체중(kg), x3 : 윙스팬(cm)

선형 회귀이므로 독립 변수(x1, x2, x3)와 종속 변수(y)의 관계는 선형이라고 가정한다. 이제 회귀 통계량을 구하기 위하여 LINEST 함수를 이용한다.

원하는 셀에 다음과 같이 입력한다.

=LINEST(E2:E18,B2:D18,TRUE,TRUE)

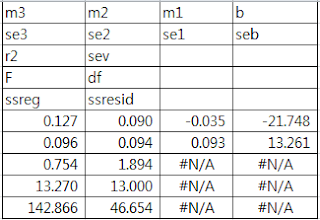
이 함수는 배열을 반환하므로 5x4 셀 범위를 택하고 F2 키를 누른 후 CTRL+SHIFT+ENTER를 누른다. 그러면 아래와 같은 통계량이 나타난다.

위의 문자 배열은 해당 통계량을 식별하기 위하여 미리 만든 것이다. 각 통계량의 의미는 아래 표와 같다.

mn, mn-1, ... , m2, m1	회귀방정식 독립변수의 계수
b	회귀방정식 절편
sen, sen-1, ..., se2, se1	계수 m1,m2,...,mn에 대한 표준 오차
seb	절편 b에 대한 표준 오차
r2	결정 계수 (0≤r²≤1)
sey	y 추정치의 표준오차
F	F-검정통계량
df	자유도
ssreg	회귀 제곱의 합
ssresid	잔차 제곱의 합

샤킬 오닐이 KBL에서 뛴다면 다음과 같이 회귀방정식에 독립변수(x1, x2, x3)=(216, 151, 229)를 넣고 계산하면 된다. 추정치는 y=13.5 즉, 경기당 평균 13.5개의 리바운드로 리그 1위가 예상된다.

​y = m1x1 + m2x2 + m3x3 + b = 13.5

위와 같이 직접 계산하는 대신 TREND 함수를 써서 바로 구할 수도 있다.

E19=TREND(E2:E18,B2:D18,B19:D19,TRUE)

이번에는 추정이 유용한지 F-검정을 통하여 알아 본다. F-분포의 자유도는 다음식으로 구한다.

\(d1=n-df-1=17-13-1=3,\ d2=df=13\)

유의수준 α가 0.05이면 F(α)=3.411 이므로 F(α)\(<\)F-검정통계량  이다. 따라서 위의 추정은 유용하다고 판단된다.

FDIST(3.411, 3, 13)=0.05