Gradient Tensor of Vector in Cylindrical Coordinates

Cylindrical coordinate system is not instinct as rectangular one, therefore vector gradient is derived as below.

Each gradient tensor of vector v in rectangular coordinates is expressed like following. Note $\nabla_i$ is the component $i$ of del operator.

${\bf v}=u{\bf i}+v{\bf j}+w{\bf k}$

$\begin{align}\nabla{\bf v}_{xx}=\nabla_x {\bf v\cdot i}=\frac{\partial {\bf v}}{\partial x}\cdot {\bf i}=\frac{\partial}{\partial x}(u{\bf i}+v{\bf j}+w{\bf k})\cdot {\bf i}=\frac{\partial u}{\partial x}\end{align}$
$\begin{align}\nabla{\bf v}_{xy}=\nabla_y {\bf v\cdot i}=\frac{\partial {\bf v}}{\partial y}\cdot {\bf i}=\frac{\partial}{\partial y}(u{\bf i}+v{\bf j}+w{\bf k})\cdot {\bf i}=\frac{\partial u}{\partial y}\end{align}$
$\cdot\cdot\cdot$

$\nabla {\bf v}=\left[\matrix{\nabla {\bf v}_{xx}&\nabla {\bf v}_{xy}&\nabla {\bf v}_{xz}\\\nabla {\bf v}_{yx}&\nabla {\bf v}_{yy}&\nabla {\bf v}_{yz}\\\nabla {\bf v}_{zx}&\nabla {\bf v}_{zy}&\nabla {\bf v}_{zz}}\right]=\begin{bmatrix}\Large\frac{\partial u}{\partial x}&\Large\frac{\partial u}{\partial y}&\Large\frac{\partial u}{\partial z}\\\Large\frac{\partial v}{\partial x}&\Large\frac{\partial v}{\partial y}&\Large\frac{\partial v}{\partial z}\\\Large\frac{\partial w}{\partial x}&\Large\frac{\partial w}{\partial y}&\Large\frac{\partial w}{\partial z}\end{bmatrix}$

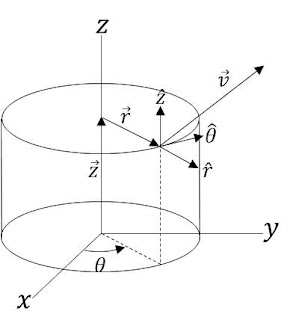
Vector in cylindrical coordinates is described as :

${\bf v}=v_r\hat r+v_\theta\hat\theta+v_z\hat z$

Derivatives of vector $\bf v$ with $r,\theta,z$ are :

$\begin{align}\frac{\partial {\bf v}}{\partial r}=\frac{\partial v_r}{\partial r}\hat r+\frac{\partial v_\theta}{\partial r}\hat\theta+\frac{\partial v_z}{\partial r}\hat z\end{align}$

$\begin{align}\frac{\partial {\bf v}}{\partial\theta}=\frac{\partial(v_r\hat r)}{\partial\theta}+\frac{\partial(v_\theta\hat\theta)}{\partial\theta}+\frac{\partial(v_z\hat z)}{\partial\theta}=\frac{\partial v_r}{\partial\theta}\hat r+v_r\hat\theta+\frac{\partial v_\theta}{\partial\theta}\hat\theta-v_\theta\hat r+\frac{\partial v_z}{\partial\theta}\hat z\end{align}$

Where each term is needed product rule. Refer to this page for unit vector variation.

$\begin{align}\frac{\partial(v_r\hat r)}{\partial\theta}=\frac{\partial v_r}{\partial\theta}\hat r+v_r\frac{\partial\hat r}{\partial\theta}=\frac{\partial v_r}{\partial\theta}\hat r+v_r\hat\theta\end{align}$

$\begin{align}\frac{\partial(v_r\hat\theta)}{\partial\theta}=\frac{\partial v_\theta}{\partial\theta}\hat\theta+v_\theta\frac{\partial\hat\theta}{\partial\theta}=\frac{\partial v_\theta}{\partial\theta}\hat\theta-v_\theta\hat r\end{align}$

$\begin{align}\frac{\partial(v_z\hat z)}{\partial\theta}=\frac{\partial v_z}{\partial\theta}\hat z+v_z\frac{\partial\hat z}{\partial\theta}=\frac{\partial v_z}{\partial\theta}\hat z\end{align}$

Lastly, the partial derivative of z direction is :

$\begin{align}\frac{\partial {\bf v}}{\partial z}=\frac{\partial v_r}{\partial z}\hat r+\frac{\partial v_\theta}{\partial z}\hat\theta+\frac{\partial v_z}{\partial z}\hat z\end{align}$

Now, each tensor term is derived as following.

$\begin{align}\nabla{\bf v}_{rr}=\nabla_r{\bf v}\cdot\hat r=\frac{\partial{\bf v}}{\partial r}\cdot\hat r=\left(\frac{\partial v_r}{\partial r}\hat r+\frac{\partial v_\theta}{\partial r}\hat\theta+\frac{\partial v_z}{\partial r}\hat z\right)\cdot\hat r=\frac{\partial v_r}{\partial r}\end{align}$

$\begin{align}\nabla{\bf v}_{r\theta}=\nabla_\theta{\bf v}\cdot\hat r=\frac{\partial{\bf v}}{r\partial\theta}\cdot\hat r=\frac{1}{r}\left(\frac{\partial v_r}{\partial\theta}\hat r+v_r\hat\theta+\frac{\partial v_\theta}{\partial\theta}-v_\theta\hat r+\frac{\partial v_z}{\partial\theta}\hat z\right)\cdot\hat r=\frac{\partial v_r}{r\partial\theta}-\frac{v_\theta}{r}\end{align}$

$\begin{align}\nabla{\bf v}_{rz}=\nabla_z{\bf v}\cdot\hat r=\frac{\partial{\bf v}}{\partial z}\cdot\hat r=\left(\frac{\partial v_r}{\partial z}\hat r+\frac{\partial v_\theta}{\partial z}\hat\theta+\frac{\partial v_z}{\partial z}\hat z\right)\cdot\hat r=\frac{\partial v_r}{\partial z}\end{align}$

$\begin{align}\nabla{\bf v}_{\theta r}=\nabla_r{\bf v}\cdot\hat\theta=\frac{\partial{\bf v}}{\partial r}\cdot\hat\theta=\left(\frac{\partial v_r}{\partial r}\hat r+\frac{\partial v_\theta}{\partial r}\hat\theta+\frac{\partial v_z}{\partial r}\hat z\right)\cdot\hat\theta=\frac{\partial v_\theta}{\partial r}\end{align}$

$\begin{align}\nabla{\bf v}_{\theta\theta}=\nabla_\theta{\bf v}\cdot\hat\theta=\frac{\partial{\bf v}}{r\partial\theta}\cdot\hat\theta=\frac{1}{r}\left(\frac{\partial v_r}{\partial\theta}\hat r+v_r\hat\theta+\frac{\partial v_\theta}{\partial\theta}\hat\theta-v_\theta\hat r+\frac{\partial v_z}{\partial\theta}\hat z\right)\cdot\hat\theta=\frac{\partial v_\theta}{r\partial\theta}+\frac{v_r}{r}\end{align}$

$\begin{align}\nabla{\bf v}_{\theta z}=\nabla_z{\bf v}\cdot\hat\theta=\frac{\partial{\bf v}}{\partial z}\cdot\hat\theta=\left(\frac{\partial v_r}{\partial z}\hat r+\frac{\partial v_\theta}{\partial z}\hat\theta+\frac{\partial v_z}{\partial z}\hat z\right)\cdot\hat\theta=\frac{\partial v_\theta}{\partial z}\end{align}$

$\begin{align}\nabla{\bf v}_{zr}=\nabla_r{\bf v}\cdot\hat z=\frac{\partial v}{\partial r}\cdot\hat z=\left(\frac{\partial v_r}{\partial r}\hat r+\frac{\partial v_\theta}{\partial r}\hat\theta+\frac{\partial v_z}{\partial r}\hat z\right)\cdot\hat z=\frac{\partial v_z}{\partial r}\end{align}$

$\begin{align}\nabla{\bf v}_{z\theta}=\nabla_\theta{\bf v}\cdot\hat z=\frac{\partial{\bf v}}{r\partial\theta}\cdot\hat z=\frac{1}{r}\left(\frac{\partial v_r}{\partial\theta}\hat r+v_r\hat\theta+\frac{\partial v_\theta}{\partial\theta}\hat\theta-v_\theta\hat r+\frac{v_z}{\partial\theta\hat z}\right)\cdot\hat z=\frac{v_z}{r\partial\theta}\end{align}$

$\begin{align}\nabla{\bf v}_{zz}=\nabla_z{\bf v}\cdot\hat z=\frac{\partial{\bf v}}{\partial z}\cdot\hat z=\left(\frac{\partial v_r}{\partial z}\hat r+\frac{\partial v_\theta}{\partial z}\hat\theta+\frac{\partial v_z}{\partial z}\hat z\right)\cdot\hat z=\frac{v_z}{\partial z}\end{align}$

Finally, we've got the all slots of the gradient of vector in cylindrical coordinates.

$\nabla{\bf v}=\left[\matrix{\nabla{\bf v}_{rr}&\nabla{\bf v}_{r\theta}&\nabla{\bf v}_{rz}\\\nabla{\bf v}_{\theta r}&\nabla{\bf v}_{\theta\theta}&\nabla{\bf v}_{\theta z}\\\nabla{\bf v}_{zr}&\nabla{\bf v}_{z\theta}&\nabla{\bf v}_{zz}}\right]=\left[\matrix{\Large\frac{\partial v_r}{\partial r}&\Large\frac{\partial v_r}{r\partial\theta}-\frac{v_\theta}{r}&\Large\frac{\partial v_r}{\partial z}\\\Large\frac{\partial v_\theta}{\partial r}&\Large\frac{\partial v_\theta}{r\partial\theta}+\frac{v_r}{r}&\Large\frac{\partial v_\theta}{\partial z}\\\Large\frac{\partial v_z}{\partial r}&\Large\frac{\partial v_z}{r\partial\theta}&\Large\frac{\partial v_z}{\partial z}}\right]$