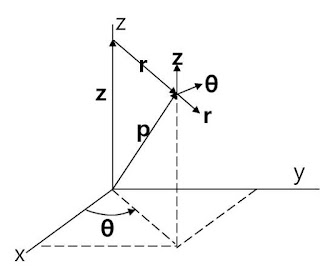
원통좌표계 벡터 변환 (Vector Transformation in Cylindrical Coordinates)

직교좌표계와 상호변환

\(r=\sqrt{x^2+y^2}\)
\(\theta={\rm Tan}^{-1}(y/x)\)
\(x=r{\rm cos}\theta\)
\(y=r{\rm sin}\theta\)

단위 벡터

원통좌표계 단위벡터는 직교좌표계와 달리 좌표의 함수이다. 따라서 직교좌표계 단위벡터와 같이 표현하면 편리하다.

\(\begin{align}\hat r=\frac{\bf r}{r}=\frac{x{\bf i}+y{\bf j}}{r}={\bf i}{\rm cos}\theta+{\bf j}{\rm sin}\theta\end{align}\)
\(\hat \theta=\hat z\times\hat r={\bf k}\times({\bf i}{\rm cos}\theta+{\bf j}{\rm sin}\theta)=-{\bf i}{\rm sin}\theta+{\bf j}{\rm cos}\theta\)
\(\hat z={\bf k}\)

단위 벡터의 좌표계 미분

위의 표현을 이용하면 다음과 같이 쉽게 단위 벡터의 좌표계 방향별 편미분을 유도할 수 있다.

\(\begin{align}\frac{\partial\hat r}{\partial r}=0\end{align}\)
\(\begin{align}\frac{\partial\hat r}{\partial\theta}=-{\bf i}{\rm sin}\theta+{\bf j}{\rm cos}\theta=\hat\theta\end{align}\)
\(\begin{align}\frac{\partial\hat r}{\partial z}=0\end{align}\)
\(\begin{align}\frac{\partial\hat\theta}{\partial r}=0\end{align}\)
\(\begin{align}\frac{\partial\hat\theta}{\partial\theta}=-{\bf i}{\rm cos}\theta-{\bf j}{\rm sin}\theta=-\hat r\end{align}\)
\(\begin{align}\frac{\partial\hat\theta}{\partial z}=0\end{align}\)
\(\begin{align}\frac{\partial\hat z}{\partial r}=0\end{align}\)
\(\begin{align}\frac{\partial\hat z}{\partial\theta}=0\end{align}\)
\(\begin{align}\frac{\partial\hat z}{\partial z}=0\end{align}\)