부정정 트러스의 최적화 문제 (Statically Indeterminate Truss Optimization)

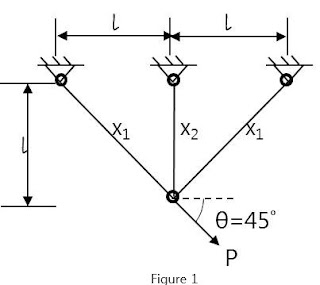
3개의 봉을 가지는 트러스 구조의 주어진 단면적 범위 내에서 최소 체적으로 허용응력 이하의 조건을 가지는 최적화 문제이다.

$x_1,\ x_2$: 봉 단면적$\left(mm^2\right),\ l=100mm,\ {\rm P}=2000N$

부정정 문제의 역학적 해법은 링크를 참조한다.

설계 문제 정식화는 다음과 같다.

Find ${\bf x}=\left\{x_1, x_2\right\}^T$

Minimize $f({\bf x})=2x_1lcos\theta+x_2l=100\sqrt{2}x_1+100x_2$ (volume)

Subject to $\begin{align}g_1({\bf x})=\sigma_1=\frac{F_1}{x_1}=P\frac{2x_1cos^3\theta+x_2(1-cos^2\theta)}{x_1(2x_1cos^3\theta+x_2)}=P\frac{\sqrt{2}x_1+x_2}{\sqrt{2}x_1(x_1+\sqrt{2}x_2)}\le 200MPa\end{align}$

                    $\begin{align}g_2({\bf x})=\sigma_2=\frac{F_2}{x_2}=P\frac{cos^3\theta}{2x_1cos^3\theta+x_2}=P\frac{1}{x_1+\sqrt{2}x_2}\le 200MPa\end{align}$

                     $1\le x_1,x_2\le 20mm^2$

다음은 엑셀 '해 찾기' 기능을 사용한 최적해이다.

최적화 기법	$x_1$	$x_2$	$f({\bf x})$	$g_1({\bf x})$	$g_2({\bf x})$
GRG 비선형	7.88	4.09	2638.96	200.00	146.31
Evolutionary	7.86	4.17	2639.01	200.00	146.55