축하중을 받는 봉의 변형(Deflections of Axially Loaded Members)
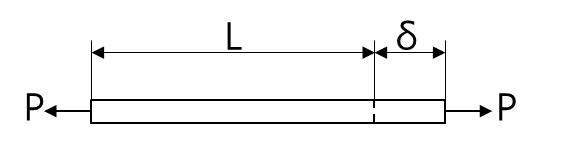
아래 그림과 같이 길이 L의 균일 단면봉이 축하중 P에 의해 인장 상태에 있다.
단면에 작용하는 균일 응력은 σ = P/A로 주어지고, 여기서 A는 단면적이다. 또한, 축방향 변형율은 ε = δ/L 이다. 여기서 δ는 축하중에 의한 늘음량이다. 선형 탄성 재질로 가정하면 후크의 법칙, σ = Eε이 적용된다. 그 다음 앞의 두식을 결합하면 봉의 늘음량에 대한 다음 공식을 얻는다.
\(\delta =\epsilon L=\dfrac{\sigma }{E}L=\dfrac{PL}{EA}\)
축하중을 받는 봉의 강성(stiffness) k는 단위 길이 변형을 발생시키는 하중으로 정의된다. 따라서 위의 식으로부터
\(k=\dfrac{EA}{L}\)
유사한 방법으로 연성(flexibility) f는 단위 하중으로 발생되는 변형량으로 정의하며 다음식과 같다.\(f=\dfrac{L}{EA}\)
\(\begin{align}\delta&=\delta_{AB}+\delta_{BC}+\delta_{CD}\\&=\frac{1}{EA}\left(P_{AB}a+P_{BC}b+P_{CD}c\right)\\&=\frac{1}{EA}\left\{\left(-P_1+P_2+P_3\right)a+\left(P_2+P_3\right)b+P_3c\right\}\end{align}\)
\(\delta=\delta_1+\delta_2=\dfrac{P_1a}{E_1A_1}+\dfrac{\left(P_1+P_2\right)}{E_2A_2}\)
일반적으로, 각각 다른 축하중과 단면을 가진 부분으로 구성된 봉의 총 변형량 δ는 다음 식으로 구할 수 있다.
\begin{align}\delta=\sum_{i=1}^n\frac{P_iL_i}{E_iA_i}\end{align}
축하중이나 단면적이 축방향으로 연속적으로 변하는 경우 위의 식을 사용할 수 없다. 대신, 아래 그림과 같이 미소요소의 늘음량를 고려해 전체 길이에 걸쳐서 적분한다.
 |
| 단면 및 충하중이 연속적으로 변화하는 봉 |
그림과 같은 사다리꼴 봉이 수직으로 매달려 있으면 자중에 의해 연속적인 분포하중을 받는다. 좌단으로부터 거리 x만큼 떨어진 길이 dx의 요소를 자를 수 있다. 이 요소의 축하중과 단면적은 x의 함수로 표현되어야 한다. 그러면 전체 늘음량은 다음과 같이 나타난다.
\begin{align}\delta=\int_0^Ld\delta=\int_0^L\frac{P_xdx}{EA_x}\end{align}
위의 식은 균일 단면봉에 대한 σ = P/A로부터 유도 되었으므로 봉의 옆면 경사각이 작을 때만 정확한 해를 준다. 요컨데, 만약 양면 사이각이 20˚이면 σ = P/A로 계산한 수직응력의 최대 오차는 엄밀해의 3% 이다. 봉의 각도가 크면 엄밀한 해법이 요구된다.
이번에는 아래와 같이 재질이 다른 2개의 원통을 동시에 압축하는 경우에 수축량을 구해 본다.
하중 P는 수직 응력과 평형을 이루고 있고 σ = P/A 로부터
\(P=\sigma_1A_1+\sigma_2A_2\)
수축량 δ은 안쪽 원기둥과 외부 원통이 동일하므로
\(\epsilon=\dfrac{\delta}{L}=\dfrac{\sigma_1}{E_1}=\dfrac{\sigma_2}{E_2}\)
\(\sigma_1=\dfrac{PE_1}{A_1E_1+A_2E_2}\quad\quad\quad\sigma_2=\dfrac{PE_2}{A_1E_1+A_2E_2}\)
\(\delta=\dfrac{\sigma_1L}{E_1}=\dfrac{\sigma_2L}{E_2}=\dfrac{PL}{A_1E_1+A_2E_2}\)
또한 변형률은
\(\epsilon=\dfrac{\delta}{L}=\dfrac{P}{A_1E_1+A_2E_2}\)





댓글
댓글 쓰기