기계공학 (Mechanical Engineering)

세계의 항공기사들에게 좀 더 나은 정보를 전달하기 위해, 국제항공학술대회를 통해 표준대기의 정의가 정립되었다. 미표준대기의 수준점(sea level) 상태는 아래 표와 같다. 성질 기호 SI단위 英단위 온도 T 288˚K 59˚F 압력 p 101.3kPa(abs) 14.696psia 밀도 \(\rho\) \(\rm1.225kg/m^3\) \(0.002377\rm slug/ft^3\) 비중량 \(\gamma\) - \(0.07651\ \rm  lbf/ft^3\) 점도 \(\mu\) \(1.781\times10^5\rm kg/m\cdot s\) \(3.719\times10^{-7}\rm lbf\cdot s/ft^2\) 미국 표준대기의 높이에 따른 온도분포가 아래 그래프에 나타나 있다. 미국표준대기의 높이에 따른 온도변화

 압력은 힘을 받는 면을 향해 수직으로 작용하는 단위면적당의 힘이다. SI 단위계에서는 \(\rm N/m^2\)의 단위를 가지며 1 \(\rm N/m^2\)는 1 Pa(Pascal)로 정의된다. 영국단위계로는 \(\rm lbf/ft^2\)(psf) 혹은 \(\rm lbf/in^2\)(psi)의 단위를 갖는다. 대기압인 1 기압(1 atm)은 101,325 Pa(14.7 psi) 혹은 1.01325 bar(1 bar=\(10^5\) Pa) 이다. 압력에는 완전진공상태를 기준으로 하여 측정되는 절대압력 (absolute pressure)과 대기압을 기준으로 하여 측정되는 계기압력 (gage pressure)의  두가지가 있다. 예를 들면, 공기탱크 내부의 계기압력이 50 kPa 이고 주위 대기압이 100 kPa 이면 탱크 내의 절대압력은 150 kPa 이다. 영국단위계에서는 압력 단위 끝에 절대압력은 a를 붙이고(psia) 계기압력의 경우에는 g를 붙인다(psig). 정지한 유체 내 임의의 점에서의 압력은 방향에 관계없이 일정하다. 이를 증명하기 위해 아래와 같은 유체 내의 미소요소를 생각한다. z 방향은 x-y 평면에 수직한 방향이다. 정지 유체이므로 압력과 중력만이 작용한다. 중력은 y의 음의 방향이고, 요소의 z 방향 길이는 1 이라고 하자. 정지된 물체에 대해서는 각 방향의 힘의 평형 이 성립하므로, 우선 x 방향의 평형식은 다음과 같다. \(\sum {\rm F}_x=p_xdy-\left(p\dfrac{dy}{\sin\theta}\right)\sin\theta=0\) 이 식으로부터 \(p=p_x\)가 됨을 알 수 있다. y 방향 평형식은 다음과 같다. \(\sum{\rm F}_y=p_ydy-\left(p\dfrac{dx}{\cos\theta}\right)\cos\theta-\dfrac{\gamma}{2}dxdy=0\) 여기서 마지막 항은 중력 W를 나타낸다. 이 식을 정리하면 다음과 같다. \(p_y-p-\dfrac{\gamma}{2}dy=0\)

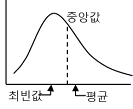
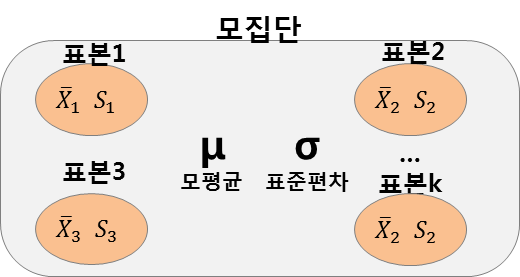
기술통계에서 데이터를 요약하는 방법으로는 중심척도, 산포척도 등의 기술통계량을 사용하여 값으로 요약하는 방법과 히스토그램, 상자그림 , 버블도 등 도식적으로 요약하는 방법이 있다. ◆ 기술통계량 (Descriptive Statistics) 중심척도 -산술평균 (Arithmetic Mean) \(\begin{align}\overline X={1\over n}\sum_{i=1}^nx_i\end{align}\) 상가평균이라고도 하며 주어진 데이터의 합을 데이터의 개수로 나눈 것이다. 평균에서 모든 편차의 합은 영이다. \(\begin{align}\sum_{i=1}^n\left(x_i-\overline X\right)=0\end{align}\) 계산상의 편리함으로 널리 사용되지만 극단적인 값의 영향을 많이 받는다. 따라서 크기 순으로 정렬한 데이터의 양 끝 일부를 제외한 나머지 데이터로 계산한 절사평균이 쓰이기도 한다. 엑셀 함수 : average(number1, [number2], ...), ※ 절사 평균 : trimmean(array, percent) 중심척도 -기하 평균 (Geometric Mean) \(\begin{align}G=\sqrt[n]{x_1\times x_2\times\cdot\cdot\cdot\times x_n}\end{align}\) 주어진 데이터를 모두 곱하고 데이터의 개수만큼 제곱근을 취한 것이다. 인구변동률, 물가변동률 같은 변화율이나 평균을 구할 때 사용한다. 상승평균이라고도 한다. 엑셀 함수 : geomean(number1, [number2], ...) 중심척도 -조화 평균 (Harmonic Mean) \(\begin{align}H=\frac{n}{\begin{align}\sum_{i=1}^n{1\over x_i}\end{align}}\end{align}\) 주어진 데이터의 역수의 산술평균한 값에 역수를 취한 것이다. 속도와 같은 시간적으로 계속하여 변하는 변량에 사용한다. 엑셀 함수  : harmean(number1, [nu

통계적 추정 표본 의 특성을 나타내는 통계량을 기초로 하여 모집단의 특성인 모수를 추측하는 통계적 분석을 말한다. 점추정 모수를 단일치로 추측한다. 틀릴 가능성이 크며 신뢰도를 확률로 나타낼 수 없다. 구간추정 모수를 포함할 것으로 예측되는 구간을 추측한다. 모수 추정치와 신뢰도를 확률로 구할 수 있다. 점추정 모수의 점추정량은 다음과 같이 표본 통계량의 단일치로 추정한다. (1) 모평균         ← 표본평균 (\(\overline X\)) (2) 모분산         ← 표본분산 (\(S^2\)) (3) 모표준편차 ← 표본표준편차 (\(S\)) 표준오차 (Standard Error) 모평균(\(\mu\))과 개별 표본평균\(\left(\overline{X}_1,\,\overline{X}_2,\,\cdot\cdot\cdot,\overline{X}_k\right)\)의 차이를 추정한 값이다. 표본평균이 모평균을 기준으로 얼마나 흩어져 있는 지를 나타낸다. 즉, 표본평균의 표준편차이다. 중심극한정리 에 의해 표준오차는 다음식으로 표현된다. \(SE=\dfrac{\sigma}{\sqrt{n}}\) 여기서 n은 표본평균에 사용된 데이터의 개수 신뢰수준 (Confidence Level) 구간추정 시 해당 구간 내에 추정하고자 하는 모수가 있을 확률 이다. 신뢰수준 95%는 해당 모수를 100번 추정했을 때 신뢰구간 내에 95번 정도 포함된다는 의미이다. 일반적으로 90%, 95%, 99% 를 사용한다. 신뢰구간 (Confidence Interval) 해당 신뢰수준에서 모수가 포함될 구간을 말한다. 신뢰구간이 크면 모수의 추정범위가 커지므로 정보로서의 가치가 떨어진다. 신뢰수준이 정확성과 관련은 있으나 그 자체가 정확성을 나타내는 것은 아니다. 모수를 더 정확하게 추정하려면 신뢰구간의 폭을 줄이는 것이 필요하다. 신뢰구간 추정 모수에 맞는 확률분포 와