기술 통계 (Descriptive Statistics)

기술통계에서 데이터를 요약하는 방법으로는 중심척도, 산포척도 등의 기술통계량을 사용하여 값으로 요약하는 방법과 히스토그램, 상자그림, 버블도 등 도식적으로 요약하는 방법이 있다.

◆ 기술통계량 (Descriptive Statistics)

중심척도 -산술평균 (Arithmetic Mean)

$\begin{array}{r} \overset{―}{X} = \frac{1}{n} \sum_{i = 1}^{n} x_{i} \end{array}$

상가평균이라고도 하며 주어진 데이터의 합을 데이터의 개수로 나눈 것이다. 평균에서 모든 편차의 합은 영이다.

$\begin{array}{r} \sum_{i = 1}^{n} (x_{i} - \overset{―}{X}) = 0 \end{array}$

계산상의 편리함으로 널리 사용되지만 극단적인 값의 영향을 많이 받는다. 따라서 크기 순으로 정렬한 데이터의 양 끝 일부를 제외한 나머지 데이터로 계산한 절사평균이 쓰이기도 한다.

엑셀 함수 : average(number1, [number2], ...), ※ 절사 평균 : trimmean(array, percent)

중심척도 -기하 평균 (Geometric Mean)

$\begin{array}{r} G = \sqrt[n]{x_{1} \times x_{2} \times \cdot \cdot \cdot \times x_{n}} \end{array}$

주어진 데이터를 모두 곱하고 데이터의 개수만큼 제곱근을 취한 것이다. 인구변동률, 물가변동률 같은 변화율이나 평균을 구할 때 사용한다. 상승평균이라고도 한다.

엑셀 함수 : geomean(number1, [number2], ...)

중심척도 -조화 평균 (Harmonic Mean)

$\begin{array}{r} H = \frac{n}{\begin{matrix} \sum_{i = 1}^{n} \frac{1}{x_{i}} \end{matrix}} \end{array}$

주어진 데이터의 역수의 산술평균한 값에 역수를 취한 것이다. 속도와 같은 시간적으로 계속하여 변하는 변량에 사용한다.

엑셀 함수 : harmean(number1, [number2], ...)

중심척도 -중앙값 (Medoan)

주어진 데이터를 크기 순으로 배열하였을 때 중앙에 위치한 수치이다. 극단적인 값의 영향을 받지 않으므로 분포의 모양이 비대칭일 경우 중앙값을 사용하는 것이 산술평균이나 최빈값 보다 자료의 대표성을 높일 수 있다. 산술평균과 최빈값 사이에 위치하며 분포가 대칭인 경우 산술평균과 일치한다.

엑셀 함수 : median(number1, [number2], ...)

중심척도 -최빈값 (Mode)

주어진 데이터 중 출현빈도가 가장 높은 값이다. 중앙값과 같이 극단적인 값의 영향을 받지 않으며 경우에 따라 하나도 없거나 2개 이상 존재할 수도 있다.

엑셀 함수 : mode(number1, [number2], ...)

산포척도 -범위 (Range)

주어진 데이터 중 최대값과 최소값의 차이이다. 가장 간단한 산포도이며 적은 표본을 취급할 때 편리하다. 극단적인 최대값 또는 최소값에 크게 영향을 받는다.

엑셀 함수 : max(array) - min(array)

산포척도 -4분위 범위 (Interquartile Range)

주어진 데이터를 크기 순서로 나열했을 때 제 3사분위수와 제1사분위수 간의 차이이다. 극단적인 값에 영향을 받지 않으며 대표값이 중앙값일 때 사용되는 산포척도이다. 1사분위수(First Quartile)는 주어진 데이터를 크기 순으로 나열하였을 때 누적 백분율이 25%에 해당하는 값이며 3사분위수(Third Quartile)는 75%에 해당하는 값이다.

엑셀 함수 : quartile.exc(array, 3) - quartile.exc(array, 1)

[예제] 아래와 같은 12개의 데이터에서 1사분위수, 3사분위수를 각각 구하여라.

1	23
2	46
3	56
4	77
5	84
6	100
7	115
8	123
9	132
10	159
11	162
12	178

<풀이> 1사분위수를 구하기 위해 먼저 누적 백분율 25%에 해당하는 순위를 계산한다. 이어서 해당 순위의 값을 선형보간으로 구한다.

$\begin{aligned} (n + 1) \times 0.25 = 13 \times 0.25 = 3.25 \\ 1 사 분 위 수 = 56 + (77 - 56) \times 0.25 = 61.25 \end{aligned}$

3사분위수도 같은 방법으로 구하면 된다.

$\begin{aligned} (n + 1) \times 0.75 = 13 \times 0.75 = 9.75 \\ 3 사 분 위 수 = 132 + (159 - 132) \times 0.75 = 152.25 \end{aligned}$

산포척도 -분산 (Variance)

$V = \frac{\begin{array}{r} \sum_{i = 1}^{n} {(x_{i} - \overset{―}{X})}^{2} \end{array}}{n}$

편차 제곱의 평균으로 분산이 영이면 모든 데이터가 평균에 집중되어 있고, 분산이 클 수록 평균에서 멀리 떨어져 있다는 것을 의미한다.

엑셀 함수 : varp(number1, [number2], ...)

산포척도 -표준편차 (Standard Deviation)

$S = \sqrt{\frac{\begin{array}{r} \sum_{i = 1}^{n} {(x_{i} - \overset{―}{X})}^{2} \end{array}}{n}}$

분산에 제곱근을 취한 것으로서 원 데이터와 같은 단위를 갖는다. 분산과 마찬가지로 표준편차가 영이면 모든 데이터가 평균에 집중되어 있고, 표준편차가 클 수록 평균에서 멀리 떨어져 있다는 것을 의미한다.

엑셀 함수 : stdevp(number1, [number2], ...)

산포척도 -변동계수 (Coefficient of Variance)

$C V = \frac{S}{\overset{―}{X}}$

$여 기 서 S 는 표 준 편 차, \overset{―}{X} 는 평 균 이 다 .$

상대적인 분포의 산포척도로서, 표준편차는 평균값이 큰 데이터 쪽이 커지는 경향이 있으므로, 서로 다른 평균값을 가지는 데이터를 비교할 때는 표준편차를 평균값으로 나누어 그 차이를 조정한다.

엑셀 함수 : stdevp(array)/average(array)

왜도 (Skewness)

데이터 분포의 중심위치가 어느 쪽으로 얼마나 기울어져 있는 지의 비대칭 정도를 나타내는 측도이다.

왜도=0 : 대칭분포
왜도>0 : 좌경분포 (외쪽으로 치우침)

왜도<0 : 우경분포 (오른쪽으로 치우침)

왜도의 절대값이 클 수록 비대칭의 정도는 커진다.

엑셀 함수 : skew(number1, [number2], ...)

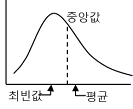
좌경분포	우경분포	대칭분포	쌍봉우리분포
●최빈값<중앙값<산술평균 ●왜도>0	●산술평균<중앙값<최빈값 ●왜도<0	●산술평균=중앙값=최빈값 ●왜도=0	●산술평균=중앙값 ●최빈값 : 2개