기계공학 (Mechanical Engineering)

엑셀은 전문 통계 프로그램이나 최적화 솔버는 아니지만 유용한 추가기능을 가지고 있고 기초적인 분석에는 충분하다고 생각된다. 이 추가기능이 메뉴에 안보이면 별도의 설정을 해 주어야 한다. 다음은 이 과정을 소개한다. ① 파일 메뉴에서 옵션을 클릭한다. ② 리본 메뉴 사용자 지정에서 개발 도구 체크박스를 선택한다(개발도구는 VBA 작업 시에도 필요하다.) ③ 확인을 누르면 개발 도구 탭이 생겼음을 알 수 있다. 여기서 추가기능을 클릭한다. ④ 팝업 창에는 사용 가능한 추가 기능 리스트가 나온다. 원하는 추가 기능을 선택한다. 예를 들면 '분석 도구'에는 통계분석을 위한 도구들이 있고 '해 찾기' 기능에는 최적화 알고리즘 사용이 가능하다. ⑤ 확인을 누르면 데이터 탭에 추가 기능 메뉴가 생성된 것을 알 수 있다.

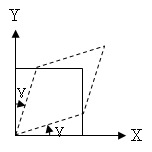
함수 f(x)는 폐구간 I=[a, b]에서 정의된 연속 인 함수이고 구간 I에서 f(x)≥0 라고 가정한다. y=f(x)의 그래프와 y축에 평행인 두 직선 x=a, x=b 및 x축으로 둘려 싸인 도형 F, 다시 말하면 부등식 a≤x ≤b, 0 ≤y ≤f(x)를 만족하는 점 (x,y)의 집합 F를 생각한다. 이 도형 F의 면적 A를 어떻게 구할 수 있는지 알아 보자. 그림 1 위의 그림 1과 같이 구간 I=[a, b] 내부에 n-1 개의 점들을 다음과 같은 순으로 취한다. \(a<x_1<x_2<\cdot\cdot\cdot<x_{i-1}<x_i<\cdot\cdot\cdot<x_{n-1}<b\) 이와 같은 분점을 취하는 방법을 구간 I=[a, b]의 하나의 분할 Δ라고 한다. 구간 I 안에 하나의 분할 Δ를 만들면 I는 n개의 소폐구간 \({\rm I}_1=[a,\,x_1],\,{\rm I}_2=[x_1,\,x_2],\,\cdot\cdot\cdot,\,{\rm I}_n=[x_{n-1},\,b]\) 으로 나누어진다. 이제 y=f(x)의 그래프와 두 직선 \(x=x_{i-1},\,x=x_i\) 및 x 축으로 둘러 싸인 도형 \({\rm F}_i\)의 면적을 \({\rm A}_i\)라 하고, 폐구간 \({\rm I}_i=[x_{i-1},\,x_i]\)에 있어서 f(x)의 최대값을 \({\rm M}_i\), 최소값을 \(m_i\)라 하자. 그림 1에서 구간 I 위에 있는 두 개의 직사각형 중 큰 것을 \(({\rm F}_i)_M\)라 하고, 작은 것을 \(({\rm F}_i)_m\)라 하면 포함 관계 \(({\rm F}_i)_m\subset{\rm F}_i\subset({\rm F}_i)_M\) 가 성립된다. 따라서 \(({\rm F}_i)_M\)의 면적을 \(({\rm A}_i)_M,\,({\rm F}_i)_m\)의 면적을 \(({\rm A}_i)_m\)라 하면 \(m_i(x_i-x_{i-1})\le{\rm A}_i\le

순수전단이란 물체가 3차원적으로 균일하게 납작해지는 변형을 말한다. 이것은 아래 그림과 같이 물체가 한 방향으로 늘어나는 동시에 수직방향은 줄어드는 비회전 변형률의 예이다. 고무와 같은 연성 재질의 순수전단은 종종 초탄성(hyperelastic) 및 파괴역학(fracture mechanical) 거동을 특성화하기 위해 사용된다. 순수전단은 강체회전(rigid body rotation)을 수반하지 않는다는 점에서 단순전단(simple shear)과는 다르다. 순수전단 위의 그림과 같은 순수전단의 변형 후 위치벡터 p (x, y) 각 성분은 다음과 같이 정의된다. \(\begin{split}x=X+\gamma Y\\y=\gamma X+Y\end{split}\) 따라서 변형구배(deformation gradient)는 다음과 같이 대칭행렬이며 이것은 강체회전이 없다는 것을 의미한다. \({\bf F}=\begin{bmatrix}\frac{\partial x}{\partial X}&\frac{\partial x}{\partial Y}\\\frac{\partial y}{\partial X}&\frac{\partial y}{\partial Y}\end{bmatrix}=\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}\) 위의 결과로부터 그린변형률(Green strain)을 정의에 따라 구할 수 있다. \(\begin{split}{\bf E}&={1\over2}({\bf F}^T\cdot {\bf F}-{\bf I})\\&={1\over2}\left\{\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}\begin{bmatrix}1&\gamma\\\gamma&1\end{bmatrix}-\begin{bmatrix}1&0\\0&1\end{bmatrix}\right\}\\&={1\over2}\left\{\begin

실험계획법 결과분석의 첫번째 단계는 인자 및 특성치 간 서로 영향을 주는지 파악하고 그 경향을 알아내는 것이다. 산포도(Scatter Plot)은 인자//특성치 분포를 2차원 투영시켜 상관 관계를 분석할 수 있는 도구이다. 산포도 (Scatter Plot) ① \(x_1\)과 \(x_2\)는 서로 영향을 주지 않는다. ② \(x_2\)와 y는 음(negative)의 선형관계에 있다. ③ \(x_1\)과 y는 2차 관계에 있다. 상관계수(Correlation Coefficient)는 두 확률변수의 공분산 크기에 대한 의존도를 제거하기 위하여 공분산을 두 확률변수의 곱으로 나눈 것이다. \(Corr(X, Y)=\rho_{X,Y}=\dfrac{cov(X,Y)}{\sigma_X\sigma_Y}\) 상관계수는 인자/특성치 간 선형관계를 나타내며 0.6 이상이면 선형 상관성이 있는 것으로 판단한다. 상관계수는 선형 상관성만 표현하므로 비선형 관계는 판단할 수 없다. 상관계수 (Correation Coeficient) [적용 예]   차종별 시험/해석 간 특성치가 다음과 같을 때 상관계수를 구하고 상관관계를 판단하라. 차종 A B C D E F G H I J 시험 10.50 20.00 25.25 37.11 19.00 15.48 22.00 30.32 9.10 18.00 해석 12.00 22.49 21.00 29.00 18.81 15.96 25.60 31.00 12.33 15.78 엑셀의 CORREL(array1, array2) 함수를 활용하여 상관계수를 구하고 분산형 차트로 가시화한다. 시험/해석 간 산포도와 상관계수 시험/해석 간 상관계수가 0.91로 매우 높은 상관성을 나타낸다. 출처 https://www.pidotech.com

행열의 대각합은 정방행열의 대각성분들의 합이다. n차(n × n) 정방행열 A의 대각합(trace)는 아래와 같이 정의한다. \(\begin{align}{\rm tr}({\bf A})=\sum_{i=1}^n{\rm A}_{ii}={\rm A}_{kk}={\rm A_{11}+A_{22}+\cdot\cdot\cdot+A}_{nn}\end{align}\) 대각합은 다음과 같은 성질을 갖는다. \({\rm tr({\bf A+B})=A_{11}+B_{11}+A_{22}+B_{22}+\cdot\cdot\cdot+A}_{nn}+{\rm B}_{nn}={\rm A}_{jj}+{\rm B}_{kk}=\rm tr({\bf A})+tr({\bf B})\) \(\begin{align}{\rm tr}(c{\bf A})=\sum_{i=1}^{n}c{\rm A}_{ii}=c\sum_{i=1}^{n}{\rm A}_{ii}=c\cdot{\rm tr}({\bf A})\end{align}\) \({\rm tr}({\bf A})={\rm tr}({\bf A}^T)\) \(\begin{align}{\rm tr}({\bf A})=\sum_{i=1}^{n}\lambda_i\end{align}\)   여기서 λ는 행열 A 의 고유치 행열 A : m × n, 행열 B : n × m 이라고 하면 \(\begin{align}{\rm tr}({\bf AB})=\sum_{i=1}^m({\rm AB})_{ii}=\sum_{i=1}^m\sum_{j=1}^n{\rm A}_{ij}{\rm B}_{ji}=\sum_{j=1}^n\sum_{i=1}^m{\rm B}_{ji}{\rm A}_{ij}=\sum_{j=1}^n({\rm BA})_{jj}={\rm tr}({\bf BA})\end{align}\)