후크의 법칙 (Hooke's Law)
개요 (Introduction)
후크의 법칙은 선형 정방성(linear and isotropic)이다. 사실 이 법칙은 정방성이라면 비선형을 포함한 초탄성(hyperelastic) 재질의 1차 선형(1st order linearization)이라 할 수 있다. 따라서 변형률이 작다면 고무에도 적용할 수 있다. 금속의 탄성영역에서는 표준 법칙이다.
수직 성분 (Normal Component)
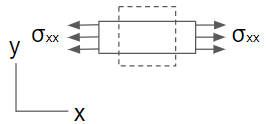
전체 모델을 얻기 위한 첫번째 단계는 단순 인장/압축으로 출발한다. 이 경우 응력-변형률 관계는
\(\sigma=E\epsilon\)
응력 및 변형률 항이 모두 1차식으므로 선형이다. 변형률은 단위가 없으므로 E는 σ와 같이 응력의 단위를 가진다.
다음 단계는 다차원으로 일반화 하는 것이다. 먼저 인장/압축의 방향을 x라 하자. 그러면 위의 식을 다음과 같이 쓸 수 있다.
\[\epsilon_{xx}={1\over E}\sigma_{xx}\]
이제 y 방향 수직응력을 추가 한다. y 방향 인장 응력은 x 방향 변형률을 감소시킨다. 따라서 위의 식을 아래와 같이 변화시킨다.
\[\epsilon_{xx}={1\over E}\sigma_{xx}-B\sigma_{yy}={1\over E}\sigma_{xx}-\nu{1\over E}\sigma_{yy}\]
만약 재질이 정방석이면 \(\sigma_{zz}\)에 대한 \(\epsilon_{xx}\)의 응답은 \(\sigma_{yy}\)와 같다. 따라서 위의 식은 다음과 같이 쓸 수 있다.
\[\epsilon_{xx}={1\over E}\left\{\sigma_{xx}-\nu\left(\sigma_{yy}+\sigma_{zz}\right)\right\}\]
| 재질 | 포아송 비 | 비고 |
| 폼 | ~0 | 무시 가능 |
| 유리 | ~0.2 | 취성 |
| 강 | ~0.3 | 강종에 따라 소폭(%) 변화 |
| 알루미늄 | 0.33 | 면심입방구조(FCC) 금속 |
| 구리 | ||
| 니켈 | ||
| 고무 | 0.5 | 비압축성 |
인장 시 후크의 법칙 적용예 (Hooke's Law Tension Example)
어떻게 하면 x 방향 인장응력으로 음의 변형률을 얻을 수 있을 까?
간단하다. y와 z 방향으로 충분한 인장응력을 가하면 된다. 후크의 법칙을 취하고 변형률이 ≤0이라 하자.
\[\epsilon_{xx}={1\over E}\left\{\sigma_{xx}-\nu\left(\sigma_{yy}+\sigma_{zz}\right)\right\}\le0\]
따라서 이 경우 다음 식이 성립한다.
\[\sigma_{xx}\le\nu\left(\sigma_{yy}+\sigma_{zz}\right)\]
위의 결과는 E와는 무관하며 ν에 영향을 받는다. \(\sigma_{xx}\ge0\) 일지라도 y와 z 방향으로 충분히 인장시키면 x 방향으로 음의 변형률을 얻을 수 있다.
전체 방정식은 다음과 같다.
\(\begin{align}&\epsilon_{xx}={1\over E}\left\{\sigma_{xx}-\nu\left(\sigma_{yy}+\sigma_{zz}\right)\right\}\\&\epsilon_{yy}={1\over E}\left\{\sigma_{yy}-\nu\left(\sigma_{zz}+\sigma_{xx}\right)\right\}\\&\epsilon_{zz}={1\over E}\left\{\sigma_{zz}-\nu\left(\sigma_{xx}+\sigma_{yy}\right)\right\}\end{align}\)
3-D 후크의 법칙 예제 (3-D Hooke's Law Example)
\(\sigma_{xx}=2,\,\sigma_{yy}=3,\,\sigma_{zz}=4\) 그리고 E=10 일 때, 다음 세가지 경우의 수직 변형률을 계산하여라 : ν=0, ν=0.33, 및 ν=0.5.
ν=0 일 때
\(\begin{split}\epsilon_{xx}=2/10=0.2\\\epsilon_{yy}=3/10=0.3\\\epsilon_{zz}=4/10=0.4\end{split}\)
ν=0.33 일 때
\(\begin{split}&\epsilon_{xx}={1\over10}\left\{2-0.33(3+4)\right\}=-0.031\\&\epsilon_{yy}={1\over10}\left\{3-0.33(2+4)\right\}=\ \ \ 0.102\\&\epsilon_{zz}={1\over10}\left\{4-0.33(2+3)\right\}=\ \ \ 0.235\end{split}\)
ν=0.5 일 때
\(\begin{split}&\epsilon_{xx}={1\over10}\left\{2-0.5(3+4)\right\}=-0.15\\&\epsilon_{yy}={1\over10}\left\{3-0.5(2+4)\right\}=\ \ \ 0.00\\&\epsilon_{zz}={1\over10}\left\{4-0.5(2+3)\right\}=\ \ \ 0.15\end{split}\)
ν=0 일 때는 변형률은 응력에 직접 비례한다. ν=0.5 일 경우는 첫째로 변형률 텐서는 항상 편향 상태이다. 둘째는 \(\sigma_{xx}\)가 양수일지라도 \(\epsilon_{xx}\)항은 음수이다. 이는 종종 포아송 효과에 대한 오해를 불러 온다.
단축 인장 예제 (Uniaxial Tension Example)
\(\sigma_{xx}=2,\,E=10,\) 그리고 ν=0.5 일 때 변형률 텐서를 구하여라.
방향별 변형률 성분을 계산하면
\(\begin{split}&\epsilon_{xx}={2\over10}=0.2\\&\epsilon_{yy}=\epsilon_{zz}=-{(0.5)(2)\over10}=-0.1\end{split}\)
위의 결과로부터 변형률 텐서는
\({\boldsymbol\epsilon}=\begin{bmatrix}0.2&0.0&0.0\\0.0&-0.1&0.0\\0.0&0.0&-0.1\end{bmatrix}\)
그리고 응력 텐서는
\({\boldsymbol\sigma}=\begin{bmatrix}2&0&0\\0&0&0\\0&0&0\end{bmatrix}\)
따라서 응력이 없는 방향도 변형률을 얻을 수 있다. 이것은 또 다른 포아송 효과의 결과이다.
또 다른 중요한 점은 \(\epsilon_{xx}\)에 대한 \(\epsilon_{yy}\)과 \(\epsilon_{zz}\)의 비가 같다는 것이다. 이는 단축 인장일 때만 일어난다. 보편적이거나 포아송 비의 정의는 아니다.
전단 성분 (Shear Component)
이제 전단 응력과 변형률의 관계로 후크의 법칙을 확장한다. 전단 응력, \(\tau_{xy}\)와 전단 변형률, \(\gamma_{xy}\)를 주방향 값들을 얻기 위해 45˚로 회전시킨다.
전단응력에 대해서
\[\begin{bmatrix}\cos45^\circ&\sin45^\circ\\-\sin45^\circ&\cos45^\circ\end{bmatrix}\begin{bmatrix}0&\gamma_{xy}/2\\\gamma_{xy}/2&0\end{bmatrix}\begin{bmatrix}\cos45^\circ&-\sin45^\circ\\\sin45^\circ&\cos45^\circ\end{bmatrix}=\begin{bmatrix}\gamma_{xy}/2&0\\0&-\gamma_{xy}/2\end{bmatrix}\]
따라서 주방향 값들은
\(\sigma_1=\tau_{xy}\qquad\sigma_2=-\tau_{xy}\qquad\epsilon_1=\gamma_{xy}/2\qquad\epsilon_2=-\gamma_{xy}/2\)
양의 주변형률을 후크의 법칙에 대입하면
\[\epsilon_1={1\over E}\left\{\sigma_1-\nu(\sigma_2+\sigma_3)\right\}\qquad{\gamma_{xy}\over2}={1\over E}\left\{\tau_{xy}-\nu(-\tau_{xy})\right\}\]
정리하면 가로탄성계수에 대한 식이 유도된다.
\[G=\frac{\tau_{xy}}{\gamma_{xy}}=\frac{E}{2(1+\nu)}\]
가로탄성계수 (Shear Modulus)
고무의 ν=0.5 이므로 가로탄성계수, G는 항상 세로탄성계수, E의 1/3이다.
금속에 대해서는, 특히 FCC 구조의 경우 포아송 비는 ν=0.33 이다. 이로부터 가로탄성계수는 세로탄성계수의 3/8, 또는 37.5% 이다.
체적탄성계수 (Bulk Modulus)
변형률에 대한 식을 모두 더하면
\[\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz}=\frac{1-2\nu}{E}\left(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}\right)\]
\((\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})\)은 체적변형률(volumetric strain), \(\epsilon_{\rm vol}=\Delta V/V\) 이다. 그리고 \((\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\)은 정수압. \(\sigma_{\rm H}\)의 3배이다.따라서 위의 식은 다음과 같이 된다.
\[\epsilon_{\rm vol}=\frac{3(1-2\nu)}{E}\sigma_{\rm H}\]
그리고 \(\epsilon_{\rm vol}\)에 대한 \(\sigma_{\rm H}\)의 비는 체적탄성계수, K라고 한다.
\[K=\frac{\sigma_{\rm H}}{\epsilon_{\rm vol}}=\frac{E}{3(1-2\nu)}\]
이것이 세로탄성계수와 체적탄성계수 간의 중요한 관계를 나타낸다. 고무의 체적탄성계수는 크지 않지만 세로탄성계소 보다는 훨씬 크다. 따라서 그 둘의 비율은 매우 작다. 이는 고무의 포아송 비가 0.5 이어야 한다는 것을 의미한다.
체적탄성계수 예제 (Bulk Modulus Example)
강(steel)은 탄성계수가 200,000 MPa, 포아송 비 0.3으로 알려져 있다. 강의 체적탄성계수는
\[K={E\over3(1-2\nu)}={200,000\over3(1-(2)(0.3))}=166,667\ {\rm MPa}\]
알루미늄은 탄성계수가 70,000 MPa 그리고 포아송 비 0.33 이다. 체적탄성계수는 탄성계수와 동일한 것으로 계산된다.
\[K={E\over3(1-2\nu)}={70,000\over3(1-(2)(0.33))}=70,000\ {\rm MPa}\]
고무의 경우 체적탄성계수는 1,000 MPa 정도이다. 강이나 알루미늄 보다 훨씬 작기 때문에 실제로 금속 보다 휠씬 더 압축성이다. 하지만 그의 체적탄성계수가 가로 또는 세로탄성계수 보다 몇 자리수는 더 크기 때문에 비압축성으로 간주된다.
행열 및 텐서 표기법 (Matrix & Tensor Notation)
후크의 법칙은 행열 및 텐서 표기법으로 각각 다음과 같이 쓸 수 있다.
\[\boldsymbol\epsilon={1\over E}\left\{(1+\nu)\boldsymbol\sigma-\nu{\bf I}{\rm tr}(\boldsymbol\sigma)\right\}\qquad\epsilon_{ij}={1\over E}\left\{(1+\nu)\sigma_{ij}-\nu\delta_{ij}\sigma_{kk}\right\}\]
모든 행열을 풀어 쓰면
\[\begin{bmatrix}\epsilon_{11}&\epsilon_{12}&\epsilon_{13}\\\epsilon_{21}&\epsilon_{22}&\epsilon_{23}\\\epsilon_{31}&\epsilon_{32}&\epsilon_{33}\end{bmatrix}={1\over E}\left\{(1+\nu)\begin{bmatrix}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}\end{bmatrix}-\nu\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}(\sigma_{11}+\sigma_{22}+\sigma_{33})\right\}\]
개별 성분들을 정리하면 아래와 같은 각 성분들의 식이 유도된다.
\[\begin{split}&\epsilon_{11}={1\over E}\left\{\sigma_{11}-\nu(\sigma_{22}+\sigma_{33})\right\}\qquad\epsilon_{12}=\frac{1+\nu}{E}\sigma_{12}\\&\epsilon_{22}={1\over E}\left\{\sigma_{22}-\nu(\sigma_{33}+\sigma_{11})\right\}\qquad\epsilon_{31}=\frac{1+\nu}{E}\sigma_{31}\\&\epsilon_{33}={1\over E}\left\{\sigma_{33}-\nu(\sigma_{11}+\sigma_{22})\right\}\qquad\epsilon_{23}=\frac{1+\nu}{E}\sigma_{23}\end{split}\]
[주의] 변형률의 비대각 성분, \(\epsilon_{12},\,\epsilon_{23}\ \text{및}\ \epsilon_{31}\)은 공학 전단 변형률의 1/2 값이다. 즉, \(\epsilon_{12}=\gamma_{12}/2\).
후크 법칙의 역함수 (Inverting Hooke's Law)
응력의 함수인 변형률을 반대로 응력을 변형률의 함수로 후크의 법칙을 적용해 보자.
위의 텐서 표기법으로부터 쉽게 \(\sigma_{ij}\)에 관한 식을 얻을 수 있다.
\[\sigma_{ij}=\frac{1}{1+\nu}(E\epsilon_{ij}+\nu\delta_{ij}\sigma_{kk})\]
양변에 \(\delta_{ij}\)를 곱하고 정리하면
\[\begin{split}&\delta_{ij}\sigma_{ij}={1\over1+\nu}(E\delta_{ij}\epsilon_{ij}+\nu\delta_{ij}\delta_{ij}\sigma_{kk})\\&\sigma_{kk}={1\over1+\nu}(E\epsilon_{jj}+3\nu\sigma_{kk})\\&\sigma_{kk}={E\over1-2\nu}\epsilon_{jj}\end{split}\]
위의 식을 다시 원식에 대입하면 응력에 대한 변형률의 함수식을 얻는다.
\[\sigma_{ij}={E\over1+\nu}\left(\epsilon_{ij}+{\nu\over1-2\nu}\delta_{ij}\epsilon_{kk}\right)\]
위의 식은 재질이 비압축성이면 ν=0.5 이므로 변형률 텐서로부터 응력 텐서를 구할 수 없다는 것에 유의한다.
강성 텐서 (Stiffness Tensor)
강성 텐서는 응력과 변형률의 관계를 나타내는 4등급 계수(3×3×3×3)이다.
\(\boldsymbol\sigma={\bf C}:\boldsymbol\epsilon\qquad\sigma_{ij}=C_{ijkl}\epsilon_{kl}\)
강성 텐서는 본질적으로 헬름홀츠 자유에너지(Helmholtz free energy)의 탄성 그린 변형률(Green strain) 텐서에 대한 2차 편도함수이다.
\[{\bf C}=\rho_0\frac{\partial^2\Psi}{\partial\boldsymbol\epsilon_{\rm el}^2}\]
그러나 위의 식은 수학적인 분석에는 그다지 유용하지 않다. 대신 후크의 법칙의 도함수를 취하는 편이 쉽다. 변형률에 대한 편미분을 취하기 전에 \(\epsilon_{ij}=(\epsilon_{ij}+\epsilon_{ji})/2\)로 치환하여 대칭성을 부여한다. 그 다음 편도함수를 전개하면 다음식을 얻는다.
\[\begin{align}C_{ijkl}&=\frac{\partial\sigma_{ij}}{\partial\epsilon_{kl}}\\&=\frac{\partial}{\partial\epsilon_{kl}}\left[\frac{E}{1+\nu}\left\{{1\over2}(\epsilon_{ij}+\epsilon_{ji})+\frac{\nu}{1-2\nu}\delta_{ij}\epsilon_{mm}\right\}\right]\\&=\frac{E}{1+\nu}\left\{{1\over2}(\delta_{ik}\delta_{jl}+\delta_{jk}\delta_{il})+\frac{\nu}{1-2\nu}\delta_{ij}\delta_{mk}\epsilon_{ml}\right\}\\&=\frac{E}{1+\nu}\left\{{1\over2}(\delta_{ik}\delta_{jl}+\delta_{jk}\delta_{il})+\frac{\nu}{1-2\nu}\delta_{ij}\delta_{kl}\right\}\end{align}\]
이제 위의 식은 i와 j 그리고 k와 l에 대하여 대칭성을 가진다.
강성 텐서 예제 (Stiffness Tensor Example)
\(\sigma_{11}\)에 기여하는 \(\epsilon_{11}\)의 계수, \(C_{1111}\)을 결정하라.
\[\begin{split}C_{1111}&={E\over1+\nu}\left\{{1\over2}(\delta_{11}\delta_{11}+\delta_{11}\delta_{11})+\frac{\nu}{1-2\nu}\delta_{11}\delta_{11}\right\}\\&={E\over1+\nu}\left(1+\frac{\nu}{1-2\nu}\delta\right)=\frac{E(1-\nu)}{(1+\nu)(1-2\nu)}\end{split}\]
\(C_{1111}\)는 \(\partial\sigma_{11}/\partial\epsilon_{11}\) 이고 이것은 \(\epsilon_{11}\)가 변하는 동안 \(\epsilon_{22}\)와 \(\epsilon_{33}\)가 상수로 유지된다는 것을 기억해야 한다.
이 과정의 결과로 체적 변화가 수반된다. 이것은 \(C_{1111}\)의 분모에 (1-2ν)를 가지고 있어 ν가 0.5에 근접하면 무한대로 가게 된다. 왜냐하면 재질이 비압축성이 되면 체적을 변화시키기 위한 응력은 무한대로 요구되기 때문이다.
또한 \(C_{1111}\)는 단축 인장하에서 재질의 강성을 의미하지는 않는다. 왜냐하면 이 경우 포아송 효과로 측방향 변형률이 변화하지만 편미분에서는 상수로 취급하기 때문이다.
편향 응력 및 변형률 (Deviatoric Stress & Strain)
후크의 법칙에서 편향 응력과 변형률의 관계를 알아 본다. 앞서 유도한 변형률과 응력의 대각합 관계식에 \(\delta_{ij}/3\)를 양변에 곱하면
\[{1\over3}\delta_{ij}\epsilon_{kk}=\frac{1-2\nu}{3E}\delta_{ij}\sigma_{kk}\]
이 결과는 정수압 응력과 변형률의 관계를 나타낸다. 위의 식을 후크의 법칙 원식에서 차감하면 다음식을 얻는다.
\[\begin{split}\epsilon_{ij}-{1\over3}\delta_{ij}\epsilon_{kk}&={1+\nu\over E}\sigma_{ij}-{\nu\over E}\delta_{ij}\sigma_{kk}-\frac{1-2\nu}{3E}\delta_{ij}\sigma_{kk}\\&={1+\nu\over E}\left(\sigma_{ij}-{1\over3}\delta_{ij}\sigma_{kk}\right)\end{split}\]
위의 결과의 양변은 편향 텐서를 포함하고 있으므로 아래와 같이 요약된다.
\[\epsilon'_{ij}=\frac{1+\nu}{E}\sigma'_{ij}={1\over2G}\sigma'_{ij}\]
따라서 편향 응력과 변형률은 서로 직접적인 비례 관계에 있다. 이는 후크의 법칙에 대해서, 수직 변형률 성붕에 대해서도 항상 성립한다.
위의 식은 실용적으로 다음과 같이 쓸 수도 있다.
\[\sigma'_{ij}=2G\epsilon'_{ij}\]
후크의 법칙 편향 성분 예제 (Deviatoric Example with Hooke's Law)
포아송 비, ν=0.5, 그리고 탄성계수 E=15 MPa의 고무 재질이 있다고 하자. 아래 응력 텐서에 대하여 후크의 법칙을 사용하여 변형률 상태를 계산하여라. 그 다음 편향 응력과 변형률을 구하고 서로간의 비례상수는 2G 임을 보여라.
\[\boldsymbol\sigma=\begin{bmatrix}8&2&4\\2&6&6\\4&6&4\end{bmatrix}\]
위의 응력 텐서는 상당한 양의 정수압 응력을 가지고 있다. 즉, 정수압 성분은
\[\boldsymbol\sigma_{\rm H}=\begin{bmatrix}6&0&0\\0&6&0\\0&0&6\end{bmatrix}\]
후크의 법칙을 적용하면
\[\begin{split}\begin{bmatrix}\epsilon_{11}&\epsilon_{12}&\epsilon_{13}\\\epsilon_{21}&\epsilon_{22}&\epsilon_{23}\\\epsilon_{31}&\epsilon_{32}&\epsilon_{33}\end{bmatrix}&={1\over15}\left\{(1+0.5)\begin{bmatrix}8&2&4\\2&6&6\\4&6&4\end{bmatrix}-3(0.5)\begin{bmatrix}6&0&0\\0&6&0\\0&0&6\end{bmatrix}\right\}\\&=\begin{bmatrix}0.2&0.2&0.4\\0.2&0.0&0.6\\0.4&0.6&-0.2\end{bmatrix}\end{split}\]
위의 변형률 텐서는 이미 편향 상태이다. 이는 포아송 비가 비압축성 재질의 ν=0.5 이기 때문이다.
이제 편향 응력과 변형률의 비례 관계를 보이기 위해 먼저 G를 계산한다.
\[G={E\over2(1+\nu)}={15\over2(1+0.5)}=5\ {\rm MPa}\]
따라서 2Gε'은 다음과 같다.
\[2G\boldsymbol\epsilon'=\begin{bmatrix}2&2&4\\2&0&6\\4&6&-2\end{bmatrix}\]
그리고 이를 \(\boldsymbol\sigma-\boldsymbol\sigma_{\rm H}\)과 비교하면
\(\begin{bmatrix}8&2&4\\2&6&6\\4&6&4\end{bmatrix}-\begin{bmatrix}6&0&0\\0&6&0\\0&0&6\end{bmatrix}=\begin{bmatrix}2&2&4\\2&0&6\\4&6&-2\end{bmatrix}\)
따라서 위의 식은 σ'=2Gε'를 만족한다. 이 예제는 비압축성 재질. ν=0.5에 대한 것이지만 압축성에 대해서도 동일하게 성립한다.




댓글
댓글 쓰기