함수와 그래프 (Function and Graph)

 함수라는 개념은 이공학에 있어서 매우 중요하다. 함수(函數)라는 단어의 한자를 보면 '상자함'자를 쓴 것을 알 수 있다. 초등학교 수학 시간에 상자그림이 있고 위의 구멍으로 숫자를 넣으면 상자의 규칙에 따라 아래로 다른 숫자가 나오는 것을 회상헤 본다. 이것이 내 인생에서 처음 접한 함수일 것이다.

현재의 값으로 미래를 예측할 수 있는 함수가 있다면 여러가지 문제들을 해결할 수 있을 것이다. 나도 그러한 일을 하고 있지만 문제는 정확한 함수(모형, 모델)을 만드는 것이 쉽지 않다.

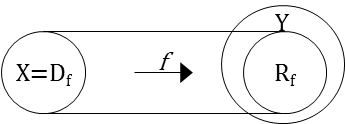
실수 전체의 집합 또는 그 부분집합 X, Y에 대하여 X의 임의의 원에 Y의 원을 한 개씩 대응시키는 규칙이 주어지면 그것을 X에서 Y로의 함수라 하고 다음과 같이 나타낸다.

f : X→Y

f에 의한 a∈X에 대응하는 Y의 원이 b이면 f의 a에서의 값은 b 이고 b=f(a)로 나타낸다. 집합 X를 f의 정의역이라 하고 \({\rm D}_f\)로 표시한다. 집합 Y는 f의 공변역이라 하고 특히 {y∈Y|y=f(x), x∈X}를 f의 치역이라 하고 \({\rm R}_f\)로 나타낸다.

집합 X의 임의의 원을 나타내는 기호를 X 위의 변수라고 한다. 함수 f가 X위의 변수 x와 Y 위의 변수 y의 대응

y=f(x)

로 주어질 때 x를 독립변수, y를 종속변수라 한다. 독립변수와 관계없는 문자를 상수라 한다.

[예제 1]  함수 \(y=ax^2(a>0)\)에서 \({\rm D}_f=(-\infty,\,\infty)\), \({\rm R}_f=[0,\,\infty)\)     ☞ 구간 표기법은 링크를 참조.

[예제 2]  함수

(1) \(y=\ \ \ \sqrt{x}\)에서 \({\rm D}_f=[0,\,\infty)\), \({\rm R}_f=[0,\,\infty)\)
(2) \(y=-\sqrt{x}\)에서 \({\rm D}_f=[0,\,\infty)\), \({\rm R}_f=(-\infty,\,0]\)

평면 상의 점 P의 좌표를 (x, y)라 할 때 함수 y=f(x)에 대한 점의 집합 \(\left\{(x,y)|y=f(x),x\in{\rm D}_f\right\}\)를 함수 f의 그래프라고 한다.

함수 f(x)의 값이 정의역 내의 모든 x에 대하여 일정하고 즉 f(x)=c(상수) 일 때, 즉 \({\rm R}_f=\left\{c\right\}\) 일 때 f를 상수함수라 한다.

함수 f가 X의 각 원에 Y의 n개의 원을 대응시킬 때 f를 n가 함수라고 한다. n≥2 인 경우를 다가함수(多價函數)라고 한다. 두 변수 x, y 사이에

\[x^2+y^2-1=0\cdots(1)\]

인 관계가 있을 때 식(1)을 y에 관하여 풀면

\[y=\pm\sqrt{1-x^2}\cdots(2)\]

만약 y의 값을 제한하면 x의 각 값에 대하여 y의 값이 두 개 정해지므로 함수

\[\begin{split}&y=f(x)=\ \ \,\sqrt{1-x^2}\ (y\ge0)\cdots(3)\\&y=g(x)=-\sqrt{1-x^2}\ (y\le0)\cdots(4)\end{split}\]

가 정해진다. (3), (4)를 합하면 (1)이 되고 2가 함수이다.

이처럼 독립변수 x와 종속변수 y 사이의 대응이 F(x, y)=0으로 주어질 때 음함수라 한다. 이 때 적당한 구간을 정하면 각각 y는 x의 함수가 되고, 그 각각의 함수를 음함수의 분지라 한다. 요컨데, (1)의 음함수의 분지는 (3), (4) 이다. 한편 y=f(x)로 표시되는 함수 f를 양함수라 한다.

함수 y=f(x)가 정의역의 모든 x에 대하여 f(-x)=f(x) 이면 f를 우함수, f(-x)=-f(x) 이면 기함수라 한다.

[예제 3] (1) \(y=x^2\), \(y=\cos{x}\)는 우함수이다.
            (2) \(y=x^5+2x\), \(y=\sin{x}\)는 기함수이다.

정의역의 모든 x에 대하여 f(x+p)=f(x)인 양수 p가 존재할 때 f를 주기함수라 하면, p 중에서 최소인 것을 주기라 한다.

[예제 4]  y=sin x, y=cos(2x-3), y=tan(πx)는 주기함수이고 각각의 주기는 2π, π, 1 이다.

함수 f가 \(x_1<x_2\) 인 임의의 \(x_1,\,x_2\)에 대하여 조건
      \(f(x_1)\le f(x_2)\)를 만족하면 증가함수

      \(f(x_1)<f(x_2)\)를 만족하면 강한 의미의 증가함수

      \(f(x_1)\ge f(x_2)\)를 만족하면 감소함수

      \(f(x_1)>f(x_2)\)를 만족하면 강한 의미의 감소함수

라 한다. 증가/감소함수를 단조함수라 한다.

《문      제》

1. 다음 각 함수의 정의역과 치역을 구하고 그래프를 그려라.
(1) f(x)=[x], [x] : x를 넘지않는 최대정수
(2) f(x)=|x|
(3) f(x)=2[x]-3

<풀이>
(1) \({\rm D}_f=(-\infty,\infty)\), \({\rm R}_f\): 정수 전체
(2) \({\rm D}_f=(-\infty,\infty)\), \({\rm R}_f=[0,\infty)\)
(3) \({\rm D}_f=(-\infty,\infty)\), \({\rm R}_f\): 홀수 전체

2. 다음 각 식으로 정의된 함수 f 중에서 우함수ㆍ기함수ㆍ주기함수ㆍ증가함수ㆍ감소함수인 것을 각각 골라라.
(1) \(f(x)=x\) : \(f(-x)=-x=-f(x)\)→기함수, \(x_1<x_2\) 이면 \(f(x_1)=x_1<f(x_2)=x_2\)→증가함수
(2) \(f(x)=x^4\) : \(f(-x)=x^4=f(x)\)→우함수
(3) \(f(x)=\frac{1}{x-1}\)
(4) \(f(x)=\sin{x}\) : \(f(-x)=\sin(-x)=-\sin{x}=-f(x)\)→기함수, \(f(x+2\pi)=f(x)\)→주기함수
(5) \(f(x)=\cos{x}\) : \(f(-x)=\cos(-x)=\cos{x}=f(x)\)→우함수, \(f(x+2\pi)=f(x)\)→주기함수
(6) \(f(x)=\tan{x}\) : \(f(-x)=\tan(-x)=\tan{x}=-f(x)\)→기함수, \(f(x+\pi)=f(x)\)→주기함수
(7) \(f(x)=-\sqrt{x}\) : \(x_1<x_2\) 이면 \(f(x_1)=-\sqrt{x_1}>f(x_2)=-\sqrt{x_2}\)→감소함수
(8) \(f(x)=[x]\) : \(x_1<x_2\) 이면 \(f(x_1)=x_1\le f(x_2)=x_2\)→증가함수

3. 다음 각 식에서 매개변수 t를 소거하여라.
(1) \(x=3t+1,\,y=t^2:t={x-1\over3},\,9y=(x-1)^2\)
(2) \(x={1-t\over t},\,y=t^2:t={1\over x+1},\,y={1\over(x+1)^2}\)
(3) \(x=t^2,\,y=t^3:x^3=t^6=y^2\)
(4) \(x={t\over1+t},\,y={t^2\over t+1}:t={x\over1-x},\,y={x^2\over1-x}\)
(5) \(x=\sqrt{t},\,y=t+{1\over t}:x^2=t,\,y=x^2+{1\over x^2}\)
(6) \(x=\frac{t^2-1}{t^2+1},\,y=\frac{2t}{t^2+1}:\)
\(t=\tan\theta,\,x=\frac{\tan^2\theta-1}{\tan^2\theta+1}=\sin^2\theta-\cos^2\theta=-\cos2\theta,\,y=\frac{2\tan\theta}{\tan^2\theta+1}=2\sin\theta\cos\theta=\sin2\theta\)
\(\therefore\ x^2+y^2=1\)