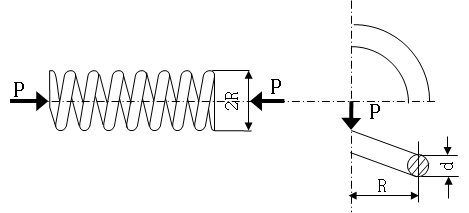
Plastic Flow Rule
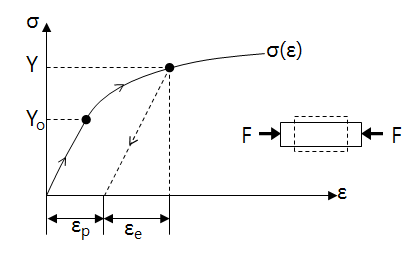
Plastic flow is used to describe the plastic behavior of materials. Plastic flow theory is based on the assumption that there exist flow laws that can be used to determine the plastic deformation of a material. The stress - strain curve above shows the plastic behavior of a typical material in uniaxial compression. The reason why compression is used instead of tension is that local necking occurs due to plastic instability in tension. On the other hand, compression does not have this phenomenon, so it can be easily converted into a true stress- true strain relationship. Strain can be decomposed into recoverable elastic strain, \(\epsilon_e\) and inelastic plastic strain, \(\epsilon_p\). The initial yield stress is \(Y_o\). If the elastic limit is not apparent, use the 0.2% offset yield strength, \(R_{p0.2}\). The above curve is a plastic hardening material, and as the plastic deformation increase, the yield stress also increases up to \(Y\). The plastic flow theory for a typical ...