코일 스프링

원통코일 스프링

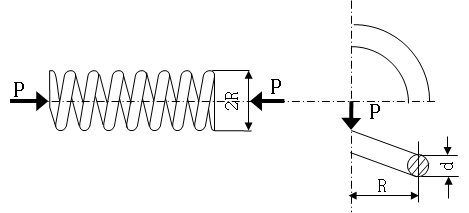
아래 그람과 같이 축방향 하중 P가 작용하고 있는 경우 평균 반지름을 R이라 하면 스프링에는 비틀림 모멘트 T=PR이 생긴다. 따라서 극단면 2차 모멘트를 J라 하고 스프링 단면 직경을 d(=2r)라 하면 다음 식이 성립한다.

\[T=PR={J\over r}\tau={\pi d^3\over16}\tau\]

윗 식으로부터 스프링 단면에 작용하는 평균 전단응력 τ가 구해지나 실제 응력은 이 값보다 크다.

즉, 코일의 단면에는 이 응력 외에 전단력, 코일 방향 압축력 및 굽힘응력 등이 작용하고 코일의 굽힘까지 고려하면 아래 그림과 같이 복잡한 응력 분포를 갖는다. 따라서 수정계수에 의해서 보정한다.

코일 스프링 단면의 응력분포

\[\tau=K{16PR\over\pi d^3}=K{8PD\over\pi d^3}=K{8C\over\pi d^2}P=K{8C^3\over\pi D^2}P\]

여기서 C=D/d=2R/d 이고 스프링 지수(指數)라 한다. 앞서 언급한 바와 같이 K를 Wahl의 수정계수라 하며, 다음과 같이 스프링 지수 C의 함수이다.

\[K={4C-1\over4C-4}+{0.615\over C}\approx{C\over C-1}+{1\over4C}\]

스프링 지수가 작으면 제작이 곤란하므로 4 이상이 보통이며, 일반적으로 4~10 범위를 취한다. Wahl의 응력수정계수는 스프링 지수가 작을 수록 갑자기 증가한다.

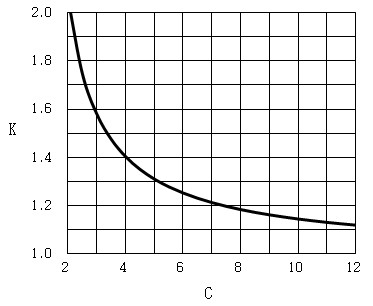원통코일 스프링의 응력수정계수

이제 스프링의 처짐을 구해본다. 비틀림 모멘트 T에 의한 비틀림 각θ는

\[\theta={Tl\over GJ}={PR\pi Dn\over GJ}\]

여기서 l=πDn은 유효길이, n은 유효감김수이다. 극단면 2차 모멘트 \(J=\pi d^4/32\) 이고, 처짐은 δ=Rθ 이므로

\[\delta=R\theta={n\pi D^3P\over4GJ}={64nPR^3\over Gd^4}={8nPD^3\over Gd^4}\]

와 같이 구해진다. 또한 스프링 상수 k는 다음과 같다.

\[k={P\over\delta}={32nR^3P^2\over Gd^4}={V\tau^3\over4K^2G}\]

여기서 \(V=(\pi d^2/4)\cdot(2\pi Rn)\)는 스프링의 부피이다.

위의 관계로부터 흡수 에너지를 크게 하려면 재료의 강도를 높여 τ를 크게 취하고 K를 작게, 즉 스프링 지수 C를 크게 해야 한다.

압축코일 스프링의 끝부를 자리(end)라 하고 아래 그림과 같이 만든다. 가장 많이 사용되는 것은 냉간 성형에서는 연삭한 벌림끝(open end)이고, 열간 성형에서는 테이퍼 가공한 맞댐끝(closed end)이다.

압축코일 스프링의 끝부 모양

압축스프링에서는 양 끝이 축에 직각이 되도록 자리를 만들어 스프링의 굽힘을 막는다. 따라서 자리 부분에서는 소선의 일부가 서로 접촉한다. 이 접촉하는 부분은 아래 그림과 같이 3/4감김, 1감김, 1(1/2)감김으로 만든다. 자리부분을 제외하고 스프링으로 유효하게 작용하는 부분의 감김수를 유효(有效)감김수라고 한다. 스프링의 양끝 지지부에 접하는 부분과 계속해서 옆의 코일과 접하고 있는 부분은 스프링으로써 기능이 없으므로 이 부분을 자리감김(end turns)이라하고, 그 수를 무효(無效)감김수라고 한다. 스프링의 한 끝에서 다른 끝까지 전체 감김수를 온감김수(total number of coils)라 하며 다음식이 성립한다.

 온감김수=유효감김수+무효감김수

압축코일 스프링의 자리 모양

유효감김수 n은 자유(自由)감김수와 같으며, 압축코일 스프링의 경우

\[n=n_t-(n_1+n_2)\]

인장코일 스프링의 경우

\[n=n_t\]

유효감김수는 일반적으로 3 이상으로 잡는다.

정하중을 받는 압축코일 스프링은 아래 그래프에서 구한다. 그래프의 값은 최대응력이므로 밀착응력 및 시험하중 시의 응력은 이 값을 넘어서는 안된다. 상용응력은 그래프의 값의 18% 이하로 한다. 인장코일 스프링은 최대응력의 64% 이하가 적당하다.

정하중에 대한 허용응력

동하중에 대한 허용응력은 피로한도 선도를 구하여 안전한 평균응력, 응력진폭을 정한다. 표면상태 등 피로한도에 미치는 영향을 고려하여 정하중보다 훨씬 낮게 취한다. 표면상태가 좋은 교번 비틀림 피로한도 \(\tau_{f1}\)은 인장강도를 \(\sigma_e\)라고 할 때

\[\tau_{f1}=(0.22\sim0.37)\sigma_e\]

이고, 반복 비틀림 피로한도 \(\tau_{f2}\)는 다음 범위에 있다.

\[\tau_{f2}=(0.83\sim0.93)\tau_{f1}\]

원추코일 스프링

코일의 지름이 변하는 스프링으로 작은 공간에서 비교적 큰 하중을 견딜 수 있다. 압축하중을 받으면 코일의 지름이 큰 부분에서 처짐이 크므로 이 부분에서 접촉이 시작된다. 전혀 접촉이 일어나지 않는 동안은 직선적으로 변화한다. 접촉이 시작되면 유효감김수가 점차로 적어지고, 또한 스프링 지수가 작아지므로 하중의 증가에 비하여 처짐의 증가는 점차 작아진다. 이 때문에 작은 공간으로 비교적 큰 하중에 견딜 수 있다.

원추코일 스프링

최대전단응력은 최대 비틀림 모멘트가 작용하는 곳, 즉 코일의 평균 지름이 최대인 \(R_2\)인 곳에 생기며 그 값은 원통코일 스프링과 동일하게 수정계수 K를 고려하면 다음과 같다.

\[\tau=K{16PR_2\over\pi d^3}\]

처짐에 대하여는 위의 그림처럼 스파이럴 곡선으로 가정하여 계산한다. 스프링 상단에서 A점까지의 감김각을 α, A점에서 스프링의 평균 반지름을 R, 이 점에 작용하는 비틀림 모멘트를 T라 하면

\[\begin{split}&R=R_1+k\alpha=R_1+\frac{(R_2-R_1)}{2\pi n}\alpha\\&T=PR=P\left\{R_1+\frac{(R_2-R_1)}{2\pi n}\alpha\right\}\end{split}\]

여기서 k 값은 \(R=R_2\) 일 때 α=2πn(n: 감김수)의 경계조건으로부터 나온다.

A점에서 소선의 미소길이 ds=Rdα에 해당하는 미소 비틀림각 dθ=Tds/GJ에 의해 발생되는 미소 처짐 dδ는

\[d\delta=Rd\theta=R{Tds\over GJ}={P\over GJ}\left\{R_1+\frac{(R_2-R_1)}{2\pi n}\alpha\right\}^3d\alpha\]

그러므로 전체의 처짐 δ는 다음과 같이 구해진다.

\[\begin{split}\delta&=\int d\delta={P\over GJ}\int_0^{2n\pi}\left\{R_1+\frac{(R_2-R_1)}{2\pi n}\alpha\right\}^3d\alpha\\&={16Pn\over Gd^4}(R_1^2+R_2^2)(R_1+R_2)\end{split}\]

서어징 (Surging)

내연기관의 밸브 스프링과 같이 반복하중이 빠른 경우, 그 반복 속도가 스프링의 고유진동수에 가
까와 지면 공진을 일으켜 스프링의 기능을 상실하고 큰 반복응력을 받아 피로파괴의 원인이 된다. 이와 같은 공진 현상을 서어징이라 한다.

압축코일 스프링의 고유진동수는 다음과 같이 구해진다.

\[f_i=a_i\sqrt{k\over  m}=a_i\sqrt{kg\over W}=a_i{d\over\pi nD^2}\sqrt{Gg\over2\gamma}\ \text{Hz}\]

여기서

w : 스프링의 무게 (kgf)
γ : 스프리의 비중량 (kgf/㎣)

d : 소선의 지름 (mm)

D : 스프링의 평균지름 (mm)

k : 스프링 상수 (kgf/mm)

n : 유효감김수

G : 가로탄성계수 (kgf/㎟)

g : 중력가속도 (9,810 mm/s²)

\(a_i\) : 계수, 양단 자유 또는 고정 i/2, 일단 자유, 타단 고정 (2i-1)/4 (i=1, 2, 3, … : 고조파 차수)

스프링의 고유진동수 f는 변동하중 진동수의 15배 이하의 경우 서어징이 일어날 가능성이 있으므로 주의해야 한다.