극관성 모멘트 (Polar Moments of Inertia)

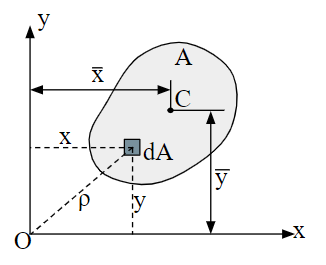
관성모멘트는 아래 그림의 x와 y축과 같이 단면 자신이 속한 평면에 놓여있는 축에 대하여 계산된다. 이제 단면이 속한 평면에 수직이고 원점 O에서 교차하는 축을 생각하자.

이 축에 대한 관성모멘트를 극관성모멘트(polar moment of inertia) $I_p$로 부른다. 이것은 다음 적분으로 정의된다.

$\begin{array}{r}{I}_p=\int {\rho }^{2}dA=\int (x^2+y^2)dA=I_x+I_y\end{array}$

여기서 ρ는 O점으로부터 면적요소 dA까지의 거리이다. 위의 식은 그림의 평면에 수직축에 대한 점 O에서의 극관성모멘트는 동일 점을 지나는 임의의 두 수직축 x와 y에 대한 관성모멘트의 합과 같다는 것을 보여준다.

극관성모멘트의 평행축 정리(parallel-axis theorem for polar moments of inertia)를 활용하면 여러점에 대한 극관성모멘트의 계산이 용이하다. 아래 그림을 참조하여 이 정리를 유도할 수 있다.

원심 O와 도심 C에 대한 극관성모멘트를 각각 $I_p$와 $I_{pc}$라 하면 다음 식으로 쓸 수 있다.

 $I_p=I_x+I_y{I}_{pc}=I_{xc}+I_{yc}$

다음으로 평행축 정리를 적용한다.

$I_x=I_{xc}+A{d}_1^2{I}_y=I_{yc}+A{d}_2^2$

위의 두 식을 더하면

$I_x+I_y=I_{xc}+I_{yc}+A(d_1^2+d_2^2)$

이제 앞의 식으로부터 $I_p$와 $I_{pc}$를 대입하고, 또한 $d^2=d_1^2+d_2^2$ 이므로 다음 식을 얻는다.

$I_p=I_{pc}+A{d}^2$

이 식은 극관성모멘트의 평행축 정리를 나타낸다: 평면상의 임의의 점 O에 대한 단면의 극관성모멘트는 도심 C에 대한 극관성모멘트에 면적과 점 O부터 C까지 거리제곱의 곱을 더한 것과 같다. 

극관성모멘트의 결정을 기술하기 위해서 아래 그림과 같은 반경 r의 원을 생각한다.

반경 ρ이고 두께 dρ인 얇은 고리모양 면적요소 dA를 취한다; 따라서 dA=2πρdρ. 이 요소의 모든 점은 원의 중심 C로부터 동일한 거리 ρ에 있기 때문에, C에 대한 요소의 극관성모멘트는 ${\rho }^{2}dA$, 또는 $2\pi {\rho }^{3}d\rho$이다. 전체 원에 대한 극관성모멘트를 얻기 위해서, 다음과 같이 적분한다.

$\begin{array}{r}{I}_p=\int {\rho }^{2}dA={\int }_0^{r}2\pi {\rho }^{3}d\rho =\frac{\pi r^4}{2}\end{array}$

원주 상 임의의 점 B에 대한 극관성모멘트는 평행축 정리로부터 얻을 수 있다.

$I_{pb}=I_{pc}+A{d}^2={\displaystyle \frac{\pi r^4}{2}}+\pi r^2(r^2)={\displaystyle \frac{3\pi r^4}{2}}$

우연의 일치로, 직경에 대한 관성모멘트를 첫번째식으로부터 쉽게 얻을 수 있다. 위의 그림으로부터

$I_x=I_y={\displaystyle \frac{I_p}{2}}={\displaystyle \frac{\pi r^4}{4}}$

원은 극관성모멘트를 적분으로 쉽게 구할 수 있는 특별한 경우이다. 그러나 공학 문제에서 접하는 대부분의 형상은 이 기법을 적용하기 어렵다. 그 대신 극관성모멘트는 통상 직교하는 두개의 축에 대한 관성모멘트를 합하여 구한다. 후자의 방법은 단면 2차모멘트와 평행축 정리 글을 참조한다.