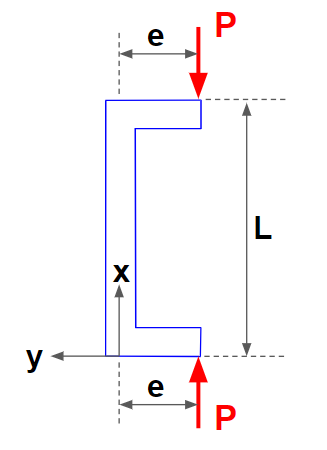
다중하중을 받는 기둥의 좌굴 (Buckling of Columns Under Multiple Loads)
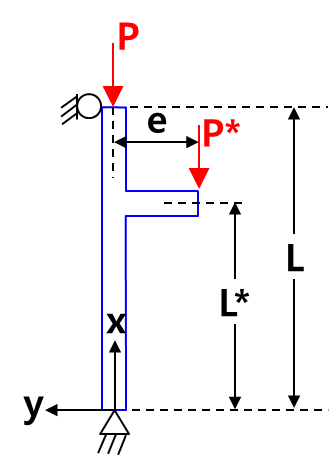
개요 (Introduction) 위의 기둥은 하나가 아닌, 두 하중을 지지한다. 하나는 오일러 좌굴이론 과 같이 기둥 중심과 일치한다. 반면에 두번째는 편심하중 조건으로 옵셋되어 있다. 이 복합하중은 복잡한 역학적 문제를 유발하며 해법은 표준 교재에서 다루고 있지 않다. 따라서, 본 글에서 그 풀이 과정과 해의 특징을 알아본다. 반력 (Reaction Forces) 첫번째 단계로 기둥의 반력을 결정하기 위해 하중과 모멘트를 합한다. 이를 통해 하단에서 윗 방향으로 수직반력 P+P*, 그리고 편심하중 P*으로 인한 모멘트 P*e에 대항하는, 크기가 같고 방향이 반대인 횡방향 하중 P*e/L가 양단에 작용한다. 굽힘모멘트 (Bending Moments) 모든 좌굴문제가 그렇듯이, 출발점은 표준 보의 굽힘 미분방정식 이다. \[EIy''=M\] M에 대한 표현은 L* 위와 아래 부분이 각각 상이하다. 따라서, 먼저 L* 위의 기둥에 대한 미분방정식을 정의하고, 다음으로 아래 부분에 대한 미분방정식을 정의 한다. 위의 그림은 기둥 상부의 자유물체도(FBD)를 보여준다. 내부힘들은 흑생으로, 외부힘들은 적색으로 표시하였다. 잘라진 면의 모멘트 총합으로부터 아래의 방정식이 유도된다. \[\text{Top}:\ M={P^*e\over L}(L-x)-Py\] 여기서, y는 기둥의 횡방향 처짐이다. Top 라벨은 이것은 L* 위의 구간에만 적용된다는 표시이다. 위의 그림은 기둥 하부의 자유물체도이다. 다시 단면부의 모멘트 총합으로부터 아래 미분방정식을 얻는다. \[\text{Bottom}:\ M=-{P^*e\over L}x-(P+P^*)y\] Bottom 라벨은 이것은 L* 아래 구간에만 적용된다는 표시이다. 지배 미분방정식 (Governing Differential Equation) 굽힘모멘트 식을 보의 굽힘 미분방정식, EIy''=M에 대입하고 정리하면 다음과 같다. \[\begin{align}&\text{Top}:\ EIy...