다중하중을 받는 기둥의 좌굴 (Buckling of Columns Under Multiple Loads)

개요 (Introduction)

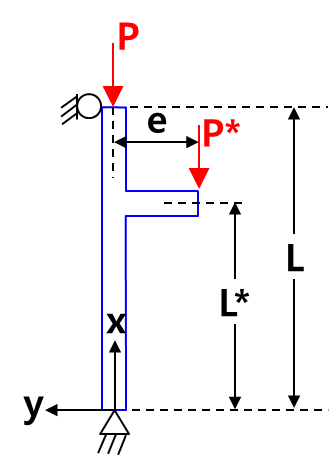
위의 기둥은 하나가 아닌, 두 하중을 지지한다. 하나는 오일러 좌굴이론과 같이 기둥 중심과 일치한다. 반면에 두번째는 편심하중 조건으로 옵셋되어 있다. 이 복합하중은 복잡한 역학적 문제를 유발하며 해법은 표준 교재에서 다루고 있지 않다. 따라서, 본 글에서 그 풀이 과정과 해의 특징을 알아본다.

반력 (Reaction Forces)

첫번째 단계로 기둥의 반력을 결정하기 위해 하중과 모멘트를 합한다. 이를 통해 하단에서 윗 방향으로 수직반력 P+P*, 그리고 편심하중 P*으로 인한 모멘트 P*e에 대항하는, 크기가 같고 방향이 반대인 횡방향 하중 P*e/L가 양단에 작용한다.

굽힘모멘트 (Bending Moments)

모든 좌굴문제가 그렇듯이, 출발점은 표준 보의 굽힘 미분방정식이다.

\[EIy''=M\]

M에 대한 표현은 L* 위와 아래 부분이 각각 상이하다. 따라서, 먼저 L* 위의 기둥에 대한 미분방정식을 정의하고, 다음으로 아래 부분에 대한 미분방정식을 정의 한다.

위의 그림은 기둥 상부의 자유물체도(FBD)를 보여준다. 내부힘들은 흑생으로, 외부힘들은 적색으로 표시하였다. 잘라진 면의 모멘트 총합으로부터 아래의 방정식이 유도된다.

\[\text{Top}:\ M={P^*e\over L}(L-x)-Py\]

여기서, y는 기둥의 횡방향 처짐이다. Top 라벨은 이것은 L* 위의 구간에만 적용된다는 표시이다.

위의 그림은 기둥 하부의 자유물체도이다. 다시 단면부의 모멘트 총합으로부터 아래 미분방정식을 얻는다.

\[\text{Bottom}:\ M=-{P^*e\over L}x-(P+P^*)y\]

Bottom 라벨은 이것은 L* 아래 구간에만 적용된다는 표시이다.

지배 미분방정식 (Governing Differential Equation)

굽힘모멘트식을 보의 굽힘 미분방정식, EIy''=M에 대입하고 정리하면 다음과 같다.

\[\begin{align}&\text{Top}:\ EIy''+Py={P^*e\over L}(L-x)\\&\text{Bottom}:\ EIy''+(P+P^*)y=-{P^*e\over L}x\end{align}\]

두 미분방정식 모두 비동차(nonhomogeneous) 방정식이다. 따라서, 이들의 해는 동차(homogeneous)와 특수부(particular parts)를 갖는다. 일반해는 다음과 같다.

\[\begin{align}&\text{Top}:\ y^{top}=T\sin\left(\sqrt{P\over EI}x\right)+U\cos\left(\sqrt{P\over EI}x\right)+{P^*\over P}\left(1-{x\over L}\right)e\\&\text{Bottom}:\ y^{bot}=B\sin\left(\sqrt{P+P^*\over EI}x\right)+C\cos\left(\sqrt{P+P^*\over EI}x\right)-{P^*\over P+P^*}\left({x\over L}\right)e\end{align}\]

여기서 T, U, B 및 C는 경계조건으로부터 결정되는 적분상수이다.

경계조건 (Boundary Conditions)

위의 두 방정식에서 4개의 계수, T, U, B 및 C를 결정하기 위해 4개의 경계조건이 필요하다. 각 경계조건으로부터 계수를 구하면 다음과 같다.

1. \(y^{top}(L)=0\) : 상단, x=L에서 기둥의 처짐은 영이다.

\[\begin{align}&\text{Top}:\ 0=T\sin\left(\sqrt{P\over EI}L\right)+U\cos\left(\sqrt{P\over EI}L\right),\ U=-T\tan\left(\sqrt{P\over EI}L\right)\\&y^{top}=T\left\{\sin\left(\sqrt{P\over EI}x\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}x\right)\right\}+{P^*\over P}\left(1-{x\over L}\right)e\end{align}\]

2. \(y^{bot}(0)=0\) : 하단, x=0에서 기둥의 처짐은 영이다.

\[\text{Bottom}:\ C=0,\ y^{bot}=B\sin\left(\sqrt{P+P^*\over EI}x\right)-{P^*\over P+P^*}\left(x\over L\right)e\]

3. \(y^{top}(L^*)=y^{bot}(L^*)\) : L* 에서 상부(top)와 하부(bottom)의 해는 연속(continuous) 이다.

\[T\left\{\sin\left(\sqrt{P\over EI}L^*\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}L*\right)\right\}+{P^*\over P}\left(1-{L^*\over L}\right)e=B\sin\left(\sqrt{P+P^*\over EI}L^*\right)-{P^*\over P+P^*}\left(L^*\over L\right)e\]

4. \(y^{top}(L^*)=y^{bot}(L^*)\) : L*에서 상부(top)와 하부(bottom)의 기울기는 연속(continuous)이다.

\[T\sqrt{P\over EI}\left\{\cos\left(\sqrt{P\over EI}L^*\right)+\tan\left(\sqrt{P\over EI}L\right)\sin\left(\sqrt{P\over EI}L^*\right)\right\}-{P^*\over P}\left(e\over L\right)=B\sqrt{P+P^*\over EI}\cos\left(\sqrt{P+P^*\over EI}L^*\right)-{P^*\over P+P^*}\left({e\over L}\right)\]

위의 식은 3번 경계조건과 함께 T와 B를 구할 수 있는 연립방정식을 준다. 대수적 풀이는 복잡하므로 실제 문제에 대해서는 수치적 기법을 사용한다.

해법 요약 (Solution Summary)

정리하면, \(y^{top}\)과 \(y^{bot}\)의 두개의 처짐 방정식(deflection equation), 그리고 상수 T와 B에 대한 두개의 경계조건 방정식(BC equation)을 얻었다.

두 처짐 방정식은

\[\begin{align}&\text{Top}:\ y^{top}=T\left\{\sin\left(\sqrt{P\over EI}x\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}x\right)\right\}+{P^*\over P}\left(1-{x\over L}\right)e\\&\text{Bottom}:\ y^{bot}=B\sin\left(\sqrt{P+P^*\over EI}x\right)-{P^*\over P+P^*}\left({x\over L}\right)e\end{align}\]

그리고 T와 B를 결정하기 위한 두 경계조건 방정식은

\[\begin{align}&T\left\{\sin\left(\sqrt{P\over EI}L^*\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}L^*\right)\right\}-B\sin\left(\sqrt{P+P^*\over EI}L^*\right)=-\left\{{P^*\over P}\left(1-{L^*\over L}+{P^*\over P+P^*}\left(L^*\over L\right)\right)\right\}e\\&T\sqrt{P\over EI}\left\{\cos\left(\sqrt{P\over EI}L^*\right)+\tan\left(\sqrt{P\over EI}L\right)\sin\left(\sqrt{P\over EI}L^*\right)\right\}-B\sqrt{P+P^*\over EI}\cos\left(\sqrt{P+P^*\over EI}L^*\right)=\left({P^*\over P}-{P^*\over P+P^*}\right){e\over L}\end{align}\]

풀이 과정은 먼저 두개의 연립 경계조건 방정식을 풀어 T와 B를 구한 후, 이들 값을 두개의 기둥의 처짐 방정식에 대입한다.

차(差)와 곱의 등식 (Differences and Products)

두 번째 경계조건 방정식의 우변은 수학적 오차로 잘못 해석될 수 있는 등가의 대수적 성질을 가지고 있다. 그것은 다음의 관계식이다.

\[{P^*\over P}-{P^*\over P+P^*}=\left({P^*\over P}\right)\left(P^*\over P+P^*\right)\]

놀랍게도, 두 항의 차는 그것들의 곱과 같다. 따라서 둘 중 어느식으로도 쓸 수 있다. 하지만, 계산을 할 때는 차의 공식을 쓰면 두 항이 거의 같을 경우 상당한 자리수가 버려질 수 있으므로 곱을 하는 것이 바람직하다. 이러한 경우는 P*≪P 일 때 발생할 수 있다. 따라서, 이후 경계조건 방정식에서는 곱의 형태를 쓸 것이다.

다른 형태 (Alternate Forms)

위의 식을 보다 쉽게 특성화하기 위해 아래 임계 좌굴하중에 대한 고전적 표현을 결합하여 대수적으로 적용할 수 있다.

\[P_{cr}={\pi^2EI\over L^2}\]

이 식을 이용하여 다중하중 기둥의 거동에 대한 통찰력을 추가로 가질 수 있다. 하지만 여기서 Pcr은, 이 하중에서 다중하중 기둥이 좌굴될 필요는 없는, 학문적값 임을 유념해야 한다.

대수적 과정은 다음과 같이 EI에 대하여 정리하고 양변에 제곱근을 취한다.

\[{1\over\sqrt{EI}}={\pi\over L\sqrt{P_{cr}}}\]

주목할 점은 앞의 방정식에서 1/√(EI)가 π, L 그리고 Pcr을 포함한 위의 식으로 치환될 수 있다는 것이다. 이로서 다음식을 얻는다.

\[\begin{align}&\text{Top}:\ y^{top}=T\left\{\sin\left(\pi\sqrt{P\over P_{cr}}{x\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\right)\cos\left(\pi\sqrt{P\over P_{cr}}{x\over L}\right)\right\}+{P^*\over P}\left(1-{x\over L}\right)e\\&\text{Bottom}:\ y^{bot}=B\sin\left(\pi\sqrt{P+P^*\over P_{cr}}{x\over L}\right)-{P^*\over P+P^*}\left(x\over L\right)e\end{align}\]

그리고 두 경계조건 방정식은

\[\begin{align}&T\left\{\sin\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\right)\cos\left(\sqrt{P\over P_{cr}}{L^*\over L}\right)\right\}-B\sin\left(\pi\sqrt{P+P^*\over P_{cr}}{L^*\over L}\right)=-\left\{{P^*\over P}\left(1-{L^*\over L}\right)+{P^*\over P+P^*}\left({L^*\over L}
\right)\right\}e\\&T\pi\sqrt{P\over P_{cr}}\left\{\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)+\tan\left(\pi\sqrt{P\over P_{cr}}\right)\sin\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)\right\}-B\pi\sqrt{P+P^*\over P_{cr}}\cos\left(P+P^*\over P_{cr}{L^*\over L}\right)={P^*\over P}\left(P^*\over P+P^*\right)e\end{align}\]

이 방법은 기둥의 거동 이해에 도움이 되는 유용한 무차원 변수들로 그룹화되어 있어 보다 쓸모가 있다. 무차원 개수를 줄이기 위해 아래와 같이 추가적으로 계수항을 정리할 수 있다.

\[{P+P^*\over P_{cr}}={P\over P_{cr}}+{P^*\over P_{cr}}\qquad\text{그리고}\qquad{P^*\over P+P^*}={P^*/P_{cr}\over P/P_{cr}+P^*/P_{cr}}\]

그러면 다음과 같이 가정 기본적인 무차원 비율 집합을 정의할 수 있다.

\[{P\over P_{cr}}\qquad{P^*\over P_{cr}}\qquad{L^*\over L}\]

특히, P/Pcr은 가정 중요한 무차원 변수로 볼 수 있다. 왜냐하면 다른 무엇보다 해의 특성을 지배하기 때문이다. 이 변수가 작으면, 기둥은 좌굴과는 거리가 먼 집중 모멘트, P*e를 받는 단순보(simple beam)와 같이 거동할 것이다. 그러나 커지게 되면, 그 만큼 좌굴 경향성을 갖게 된다.

기둥 처짐 예제 (Column Deflection Example)

1.5"×3.5" 단면, 100" 길이 기둥의 처짐을 2개의 하중 수준 및 3개의 편심하중 P* 위치 별로 비교한다. 단면 치수로부터 면적은 5.25 in² 이고 I는 0.9844 in⁴ 이다 탄성계수 E는 \(1.0\times10^6\ \text{psi}\) 이라고 한다. 그리고 이들로부터 임계 죄굴하중을 얻는다.

\[P_{cr}={\pi^2EI\over L^2}={\pi^2(10^2)(0.9844)\over100^2}=972\ \text{lb}\]

먼저 하중 P=500 lb 부터 시작한다. 이는 임계하중 보다 작고, 편심하중은 P*=10 lb, 편심량은 10" 이다.

마지막으로 편심하중 위치는 길이의 75%, 50% 및 25% 이다. 아래 그래프들은 기둥의 처짐 결과이다. 몇가지 주목할 점들은 :

1. 기둥의 처짐은 반대칭(antisymmetric) 이다. 요컨데, 75%의 경우 0.1" 왼쪽으로 이동한 반면, 25%는 오른쪽으로 동일량 만큼 이동하였다.
2. 50%의 경우, 처짐은 편심하중점 기준 상하로 반대칭이다.
3. 25%나 75%에 비해 50%의 처짐량은 상당히 작다.
4. 모든 경우에서 편심하중점의 처짐은 아래로 향한다.

이번에는, 하중 P만 500 lb에서 950 lb, Pcr의 98%로 증가시킨다. 처짐 결과는, 최소한 L의 25% 및 75% L* 경우, 전보다 상당히 증가한 것을 볼 수 있다. 또한, 더 이상 반대칭이 아니다. 이것은 편심하중 P* 자체가 비대칭이기 때문이다. 더우기, 편심하중 상부 압축하중은 P이고 그 하부는 P+P* 이다. 첫번째 P=500 lb 경우, 10 lb 추가하중은 임계하중 972 lb에 비해 여전히 작은 수준이다. 하지만, P=950 lb의 경우, 10 lb 추가하중은 임계하중(critical load)에 보다 가깝다.

이번에는, 편심량 e를 제외한 나머지를 상수로 고정시킨다. 다음 3개의 경우는 P=500 lb와 L의 75%에 P*가 위치한 첫번째와 유사하다. 하지만 편심량을 10", 100" a및 1000"로 취한다.

처짐은 편심량과 직접 비례하는 것에 주목한다. 사실 이것은 고전 편심 좌굴해석(classical eccentric buckling analysis)에서도 동일하므로 새로운 것은 아니다. 또한 다중하중 좌굴 방정식의 해에서도 명백히 적분상수식(constants of integration)은 e에 직접 비례한다.

응력 (Stresses)

응력을 계산하기 위해서는, 먼저 기둥을 따라 내부 굽힘모멘트를 계산해야 한다. 모멘트를 계산하는데는 두가지 방법이 있다. 첫째는 처짐 방정식의 2차 도함수를 취하고 EIy"=M에 대입하여 연계시킨다.

다른 방법은 처짐 방정식을 아래 식에 대입하는 것이다.

\[\begin{align}&\text{Top}:\ M^{top}={P^*e\over L}(L-x)-Py^{top}\\&\text{Bottom}:\ M^{bot}=-{P^*e\over L}x-(P+P^*)y^{bot}\end{align}\]

두가지 방법 모두 다음식이 유도된다.

\[\begin{align}&\text{Top}:\ M^{top}=-PT\left\{\sin\left(\sqrt{P\over EI}x\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}x\right)\right\}\\&\text{Bottom}:\ M^{bot}=-(P+P^*)B\sin\left(\sqrt{P+P^*\over EI}x\right)\end{align}\]

이 굽힘모멘트식을 응력을 구하기 위해 다음식에 대입한다.

\[\sigma_{comp}=\left|{F\over A}\right|+\left|Mc\over I\right|\]

여기서 c는 중립축(neutral axis)으로부터 최대 y값, 그리고 F는 L* 위에서는 P, 아래서는 P+P*와 같다. 그래프에서 최대 압축응력을 양의 값으로 얻기 위해 절대값을 취한다. P와 P*값도 양수로 사용한다. 기술적으로 이 응력은 압축이므로 음수라는 것에 주의한다. 그 결과는 아래와 같다.

\[\begin{align}&\text{Top}:\ \sigma^{top}={P\over A}+{P|T|c\over I}\left\{\sin\left(\sqrt{P\over EI}x\right)-\tan\left(\sqrt{P\over EI}L\right)\cos\left(\sqrt{P\over EI}x\right)\right\}\\&\text{Bottom}:\ \sigma^{bot}={P+P^*\over A}+{(P+P^*)|B|c\over I}\sin\left(\sqrt{P+P^*\over EI}x\right)\end{align}\]

다시 Pcr로 정규화하면 다음식을 얻는다.

\[\begin{align}&\text{Top}:\ \sigma^{top}={P\over A}\left[1+{A|T|c\over I}\left\{\sin\left(\pi\sqrt{P\over P_{cr}}{x\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\cos\left(\pi\sqrt{P\over P_{cr}}{x\over L}\right)\right)\right\}\right]\\&\text{Bottom}:\ \sigma^{bot}={P+P^*\over A}\left\{1+{A|B|c\over I}\sin\left(\pi\sqrt{P\over P_{cr}}{x\over L}\right)\right\}\end{align}\]

무차원 항 (Dimensionless Terms)

위의 식들은 편심 좌굴이론(eccentric buckling theory)의 그것과 매우 유사하다. 편심좌굴 결과는 Aec/I 항을 포함하는 반면에, A|T|c/I와 A|B|c/I를 포함한다. 또한, T와 B 모두 e에 비례하므로 그 상사성은 보기보다 휠씬 크다.

또한 이 방정식은 다음과 같이 압축과 굽힘의 기여를 구별한 형태로 볼 수 있다.

\[\sigma^{top}={P\over A}(1+\text{굽힘 항})\quad\text{및}\quad\sigma^{bot}={P+P^*\over A}(1+\text{굽힘 항})\]

따라서 기둥의 한지점에서 최대 압축응력은 P/A 또는 (P+P*)/A에서 출발하여 P와 P*에 의한 굽힘모멘트로 증폭(amplified)된 것이라 볼 수 있다. 양단은 회전단이므로 x=0와 x=L에서 기둥의 굽힘은 없으며 각각 σ=P/A와 σ=(P+P*)/A가 된다.

기둥 응력 예제 (Column Stress Example)

여기서 최대 압축응력은 앞의 처짐 예제와 동일 조건 (길이, 하중, 면적 등) 이다. 즉, 단면적은 1.5"×3.5", 탄성계수 \(10^6\) psi, 길이는 100", 편심량은 10", 그리고 P*=10 lb 이다. 이들로부터 계산하면 Pcr=972 lb 이다.

그래프의 첫번째 행은 P=500 lb 에 해당된다. 처짐과 같이, 응력 선도는 관점에 따라 대칭(symmetric), 또는 반대칭(antisymetric)이다. 상하단에서의 응력 수준은 각각 P/A와 (P+P*)/A 이고 모멘트는 영이가. 중간 구간에서는 굽힘에 의해 증가한다. 흥미롭게도, L*/L=50% 일 때 75% 보다 최대응력이 25%나 낮다.

처짐 예제와 같이, P만 500 lb에서 Pcr의 98%인 950 lb로 증가시킨다. 보는 바와 같이, 응력은 이제 결과적으로, 적어도 L의 25%와 75% L*인 경우, 전보다 상당히 크다. 또한, 더 이상 대칭도 아니다. 75%인 경우가 25% 보다 더 높은 응력을 가진다.

마지막으로, P가 두배로 증가되지 않았지만, 응력은 자릿수 이상 증가함에 주목한다. 이느 압축하중 950 lb가 Pcr에 매우 근접하기 때문이다. P가 Pcr에 근접할 수록 응력은 급수적으로 상승한다.

앞의 예제와 같이 편심량에 대응하여 응력을 그려볼 필요는 없다. 왜냐하면 응력은 직접적으로 처짐과 관련있고, 따라서 처짐처럼 편심량에 직접적으로 비례하게 된다.

기둥 응력 예제 심화 (More Column Stress Examples)

위의 예제의 응력에 대한 L*/L 의존성은 매우 흥미롭다. 아래 그래프는 기둥의 최대 압축응력을 L*/L의 함수로 그린 것이다. 이는 정확히 기둥높이의 50%에 편심하중이 작용할 때 최소응력이 발생함을 보여준다.

하중 P가 Pcr에 비해 작을 때는 P*가 기둥높이의 0% 또는 100%에 위치한 경우 가장 큰 최대응력이 발생한다. 하지만, P가 Pcr에 접근하면 명백히 기둥 상단 근처에 P*가 위치할 때, 비록 10 lb에 지나지 않지만, 하단에 위치할 때 보다 상당히 큰 최대응력이 발생한다.

좌굴 조건 (Buckling Criteria)

다중하중 기둥의 좌굴 조건을 P와 P*에 관하여 유도한다. 먼저 T와 B의 경계조건 방정식에서 출발한다.

두 방정식을 행열 표기법으로 쓰면

\[\begin{align}&\begin{bmatrix}\sin\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\right)\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)&-\sin\left(\pi\sqrt{P+P^*\over P_{cr}}{L^*\over L}\right)\\\pi\sqrt{P\over P_{cr}}\left\{\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)+\tan\left(\pi\sqrt{P\over P_{cr}}\right)\sin\left(\pi\sqrt{P\over P_{cr}}{L*\over L}\right)\right\}&-\pi\sqrt{P\over P_{cr}}\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)\end{bmatrix}\begin{Bmatrix}T\\B\end{Bmatrix}\\&=\begin{Bmatrix}-\left\{{P^*\over P}\left(1-{L^*\over L}\right)+{P^*\over P+P^*}\left({L^*\over L}\right)\right\}e\\\left({P^*\over P}\right)\left(P^*\over P+P^*\right)e\end{Bmatrix}\end{align}\]

위의 행열의 행열식은 특정 조건에서 영으로 될 수 있다. 이 조건에서 방정식을 만족하는 T와 B의 값은 무한대로 간다. 또한 처짐과 응력 모두 T와 B에 직접적으로 의존하므로, 역시 무한대로 간다. 이것이 좌굴 조건이다.

따라서 죄굴은 경계조건 방정식의 행열식이 영이 될 때 일어난다. 즉,

\[\begin{align}&-\pi\sqrt{P+P^*\over P_{cr}}\left\{\sin\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\right)\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)\right\}\cos\left(\pi\sqrt{P+P^*\over P_{cr}}{L^*\over L}\right)+\\&\pi\sqrt{P\over P_{cr}}\left\{\cos\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)+\tan\left(\pi\sqrt{P\over P_{cr}}\right)\sin\left(P\over P_{cr}{L^*\over L}\right)\right\}\sin\left(\pi\sqrt{P+P^*\over P_{cr}}{L^*\over L}\right)=0\end{align}\]

위의 식은 복잡해 보이지만 단순화할 수 있다. 먼저, 각 항 앞의 π를 소거한다. 그 다음, 앞의 두 √항을 하나의 \(\sqrt{P/(P+P^*)}\) 항으로 묶는다. 마지막으로, 두 항을 \(\cos(\pi\sqrt{P/P_{cr}}(L^*/L))\)와 \(\cos(\pi\sqrt{(P+P^*)/P_{cr}}(L^*/L))\)로 나눈다. 이상의 과정으로 방정식을 단순화 하면

\[\begin{align}&-\left\{\tan\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}\right)\right\}+\\&\sqrt{P\over P+P^*}\left\{1+\tan\left(\pi\sqrt{P\over P_{cr}}\right)\tan\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)\right\}\tan\left(\pi\sqrt{P+P^*\over P_{cr}}{L^*\over L}\right)=0\end{align}\]

다시, 재정렬하면 다음과 같다.

\[-\frac{\tan\left(\pi\sqrt{P\over P_{cr}}\right)-\tan\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)}{1+\tan\left(\pi\sqrt{P\over P_{cr}}\right)\tan\left(\pi\sqrt{P\over P_{cr}}{L^*\over L}\right)}=\sqrt{P\over P+P^*}\tan\left(\pi\sqrt{P\over P+P^*}{L^*\over L}\right)\]

좌변을 삼각함수 항등식을 활용하여 좀 더 단순화하고, 변수들을 무차원항, P/Pcr, P*/Pcr 및 L*/L로 묶으면 다음식을 얻는다.

\[-\tan\left\{\pi\sqrt{P\over P_{cr}}\left(1-{L^*\over L}\right)\right\}=\sqrt{P/P_{cr}\over P/P_{cr}+P^*/P_{cr}}\tan\left(\pi\sqrt{{P\over P_{cr}}+{P^*\over P_{cr}}}{L^*\over L}\right)\]

처음 식보다는 휠씬 단순하지만 여전히 수치해법을 요구한다. 하지만 이 식을 주어진 L*/L 값에서 P*/Pcr의 함수로 P/Pcr을 표현할 수 있다. 실제로 몇몇 L*/L 값에 대해서 아래 그래프로 나타내었다.

이 좌굴 조건에는 많은 중요한 측면들이 있다.

I. 고전 편심 좌굴이론과 주요 특징들을 공유한다.

A. 좌굴 임계하중 Pcr은 학문적인 값(academic value)에 불과하다. 왜냐하면 실제로 기둥의 응력이 먼저 재료의 항복 강도를 초과하므로, Pcr 이하의 하중에서 붕괴되기 때문이다(이는 고전 오일러 좌굴이론에는 편심하중이 없으므로 해당되지 않는다).

B. 좌굴 임계하중은 편심량 e에 전혀 의존하지 않는다. 좌굴 임계 방정식에 e는 존재하지 않는다. 그러나 실제로 기둥의 처짐과 응력은 편심량에 비례하기 때문에 매우 중요한 역할을 한다. 언급한 바와 같이 편심하중 기둥은 실제로 항복을 초과할 때 붕괴한다.

II. 하지만, 고전 편심 좌굴이론과 중요한 다른 점들이 있다.

A. 고전 편심하중 기둥은 편심량과 같은 다른 변수들에 독립적인 고유한 하중 Pcr 에서 좌굴되는 반면에, 다중하중 기둥에서는 그렇지 않다. 여기서는 기둥은 Pcr과 다른 사실 그 이하의 하중에서 좌굴한다. 이것이 Pcr을 더 학문적인 값으로 만들어 다중하중 기둥의 좌굴조건과 혼동하지 말아야 한다.

III. 최종적으로, 위의 그래프와 관련하여 중요한 특징들이 있다.

A. 일반적으로, L*/L이 클수록, 좌굴 임계점은 낮아진다.

B. L*/L=0 일 때, 좌굴에 대한 P*의 영향도는 없다. P*와 e값에 상관없이 기둥은 P=Pcr에서 좌굴한다. 하지만 여전히 기둥의 응력은 P*과 e에 영향을 받는다는 것을 기억해야 한다.

C. 또 다른 경계인, L*/L=1 일 때, 좌굴 임계조건은 단순히 P+P*=Pcr 이다. 다시 말해서, P와 P*는 동등한 중요도를 가지며, 그들의 합이 임계값이 된다.

D. 중간 구간에서는, P*이 증가하면 허용 P값이 감소하게 된다. 하지만 그 양은 원래 P* 값의 증가보다는 작다.

E. P*는 좌굴없이 Pcr을 상당히 초과할 수 있음에 유의한다. 하지만 그 양은 L*/L이 증가함에 따라 점점 작아진다.

F. L*/L이 70%를 초과하면 기둥의 거동은 거의 차이가 없다. 기둥 길이의 70% 이상 P+P*를 지지하면, 사실상 기둥의 전체 길이가 거동하는 것과 같다.

좌굴 예제 (Buckling Example)

100" 길이, 1.5"×3.5" 단면 기둥 (10" 편심) 예제를 좌굴이 될 때까지 해본다.

아래 왼쪽 그래프는 위의 예제 P=500 lb 경우를 다시 보여 준다. 처짐은 작으며 최대응력은 179 psi에 불과하다. 이 그래프를 기준으로 생각한다.

오른쪽 그래프는 편심하중 P*가 500 lb로 증가되었다. 이제 그 결과로 예상 처짐과 응력은 불가능할 정도로 크다. 그럼에도 P+P*가 Pcr보다 큼에도 불구하고 기둥은 아직 좌굴되지 않았다. (이론적으로는 좌굴되지 않았지만 실제로는 매우 높은 응력으로 인해 붕괴될 수 있음에 유의한다. 이것이 응력 수준이 항상 고려되야 하는 이유이다.)