편심하중을 받는 기둥의 좌굴 (Buckling of Eccentrically Loaded Columns)
개요 (Introduction)
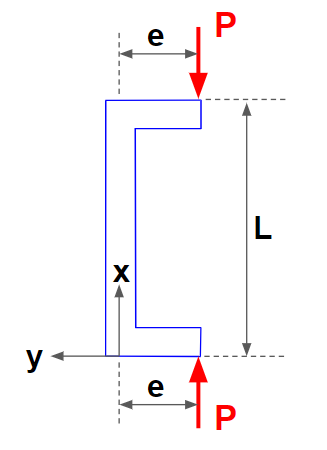
고전 기둥 좌굴이론(classical column buckling theory)과 같이, 편심하중의 기둥 좌굴 또한 독특하고 난해한 주제이다. 주어진 하중에 대하여 처짐과 응력에 대한 비선형 의존성이 있다는 점에서 독특하다. 그림에 나타낸 바와 같이 하중 P는, 그의 작용점이 기둥으로부터 거리 e 만큼 떨어져 있을 때, 편심(eccentric)되었다고 한다. 이는 통상 고전이론의 처짐에 기인한 모멘트 외에 추가로 P×e의 굽힘모멘트를 유발한다.
이론해 - 양단 회전 기둥 (Analytical Solutions - Both Ends Pinned)
편심하중 기둥의 좌굴 해석은 고전 오일러 좌굴이론과 동일하게 보의 굽힘 방정식에서 시작한다.
\[EIy''=M\]
그러나, 이번에는 M=P(y+e)가 되고, 여기서 P는 압축하중, y는 기둥의 처짐 그리고 e는 기둥의 중심으로부터 상대적으로 떨어진 거리, 편심량(eccentricity) 이다. 이 식을 위의 미분방정식 M에 대입하면 다음식이 유도된다.
\[EIy''+Py=-Pe\]
이 방정식은 다음의 일반해를 갖는다.
\[y=A\sin\left(\sqrt{P\over EI}x\right)+B\cos\left(\sqrt{P\over EI}x\right)-e\]
여기서 A와 B는 경계조건으로부터 결정되는 상수이다. 경계조건은 회전양단, x=0 및 x=L에서 y=0 이다.
첫번째 경계조건, x=0 에서 y=0, 으로부터 B=e를 얻는다. 두번째 경계조건(x=L 에서 y=0)과 삼각함수 항등식으로부터 다음을 얻는다.
\[A=e\tan\left(\sqrt{P\over EI}{L\over2}\right)\]
그러면 완전한 미분방정식의 해는 다음과 같다.
\[y=e\left\{\tan\left(\sqrt{P\over EI}{L\over2}\right)\sin\left(\sqrt{P\over EI}x\right)+\cos\left(\sqrt{P\over EI}x\right)-1\right\}\]
흥미로운 관찰 (Interesting Observations)
고전 기둥이론과 달리 이 편심하중 기둥은 간단하고, 직관적인 처짐해를 갖는다는 것은 꽤 흥미롭다. 또한 하중에 대한 처짐의 비선형성(nonlinear)도 흥미롭다. 이는 선형해석에 있어서 이례적이다.
반면에 하중에 대한 의존성과 달리 편심 e에 대하여는 선형이다. 사실, 기둥 모든 곳의 처짐은 편심량에 직접적으로 비례한다. 이 방정식은 e값이 영에 가까울 수록 고전 기둥좌굴에 근접한다는 것에 주의한다.
위의 이론해의 매력적인 점은 탄젠트 함수 의존성이다. 탄젠트 함수는 인수가 π/2에 가까울 수록 무한대로 가는 것을 기억하자. 따라서, 기둥의 처짐은 다음 조건일 때 무한대로 간다.
\[\sqrt{P\over EI}{L\over2}={\pi\over2}\]
이 식을 P에 대하여 풀면 놀라운 결과를 준다. 왜냐하면 이는 고전 비편심하중 기둥(noneccentrically loaded column)에 대한 좌굴해와 정확히 동일하기 때문이다.
\[P_{cr}={\pi^2EI\over L^2}\]
더우기, 이는 편심 e와는 독립적이다. 이것은 완전히 공학적 추론에 반(反)하는 것이다. 모든 공학적 직관으로는 편심이 증가하면 좌굴하중이 감소할 것으로 추정된다. 이것은 다음의 과정을 통해서 풀릴 것이며 공학적 추론은 만족될 것이다.
응력 (Stresses)
앞서 언급한 모순, 곧, 편심하중 기둥의 임계 좌굴하중이 편심량(eccentricity)과 독립적인 것에 대한 해법은 보의 변형에 의한 응력에서 찾을 수 있다. 이를 위해, 먼저 기둥의 응력은 다음 지배방정식으로 나타낼 수 있다.
\[\sigma={P\over A}+{My\over I}\]
여기서 P/A는 압축하중으로 인한 응력이고, My/I는 굽힘으로 인한 응력이다. y는 여기서는 기중의 처짐이 아니라 중립축으로부터 거리이다.
문제는 "기둥의 최대 압축응력은 얼마인가?" 이다. 이는 굽힘의 효과가 최대인 조건을 대입하면 찾을 수 있다. 최대 굽힘응력은 중립축으로부터 최외각, 즉, y=c에서 발생한다. 둘째는, 기둥의 길이에 걸쳐 굽힘모멘트가 최대인 곳에서 발생한다. 다시 말하면
\[\sigma_{\rm max}={P\over A}+{M_{\rm max}c\over I}\]
앞에서 M=P(y+e) 이고 여기서 y는 기둥의 처짐을 나타낸다. 따라서 최대 보의 처짐에 대응하는 굽힘모멘트 Mmax는
\[M_{\rm max}=P(y_{\rm max}+e)\]
이므로 ymax를 알 필요가 있다. 이는 x=L/2에서 발생한다. L/2에서 기둥의 처짐을 계산하면 다음식을 얻는다.
\[\begin{align}y_{\rm max}&=e\left\{\tan\left(\sqrt{P\over EI}{L\over2}\right)\sin\left(\sqrt{P\over EI}{L\over2}\right)+\cos\left(\sqrt{P\over EI}{L\over2}\right)-1\right\}\\&=e\left\{\sec\left(\sqrt{P\over EI}{L\over2}\right)\right\}\end{align}\]
이 결과를 사용하여 Mmax에 대한 식에 대입하면 σmax에 관한 식이 유도된다.
\[\begin{align}\sigma_{\rm max}&={P\over A}+{M_{\rm max}c\over I}\\&={P\over A}+{P\left[e\left\{\sec\left(\sqrt{P\over EI}{L\over2}\right)-1\right\}+e\right]c\over I}\\&=P\left\{{I\over A}+{ec\over I}\sec\left(\sqrt{P\over EI}{L\over2}\right)\right\}\end{align}\]
탄젠트 함수처럼, 시컨트 함수 또한 인수가 π/2에 근접할 수록 무한대로 간다. 또한 이 결과로 예측된 응력도 무한대로 가게 된다. 이는 새로운 기둥 붕괴조건(failure criterion), 말하자면, 기둥은 이 응력이 재료의 항복응력과 같아지면 붕괴한다 : σmax=σyield.
이 방정식을 아래와 같이 쓰는 것도 재미있다.
\[\sigma_{\rm max}=P\left\{{I\over A}+{ec\over I}\sec\left({\pi\over2}\sqrt{P\over P_{cr}}\right)\right\}\]
여기서 Pcr=π²EI/L² 이다. 이 식은 편심하중 기둥에서 Pcr은 단지 수학적 의미만 가진다는 것을 보여준다. 실제로 기둥은 σmax=σyield 일 때 붕괴하고, 이는 항상 하중이 Pcr 보다 작을 때 발생한다.
편심하중 좌굴 예제 (Eccentric Buckling Example)
아래 그래프는 단면적 100 mm²의 길이 850mm 강철봉(E=200 GPa)의 예상 응력을 보여준다. 일련의 편심량별로 하중에 대한 응력이 표시되어 있다.
| c= 10 mm L= 850 mm A= 100 mm² I=3,400 mm⁴ E= 200 GPa |
| Pcr=9,289 N |
이 그래프는 편심기둥 좌굴의 몇가지 중요한 성질을 보여준다. 거의 편심이 없는 0.1mm 곡선의 경우 응력의 이론적 한계인 P/A에 근접하다가 P=Pcr 에서 급격히 무한대로 간다. 물론, 재료는 응력이 무한대로 가면 항복하고, 곧, 붕괴될 것이며, 이것은 P=Pcr에서 붕괴되는 비편심 좌굴이론(noneccentric buckling theory)와 일치한다.
둘째로, 응력이 급격히 증가하는 시점의 하중은 옵셋 e의 증가에 따라 감소한다. 그러므로 어떠한 편심하중 기둥도 어느 시점에서는 응력이 항복강도를 초과할 것이기 때문에 P가 Pcr에 도달하기 전에 붕괴할 것이다. 이것은 Pcr이 e에 대해 독립일지라도 직관적으로 이해할 수 있는 편심하중 기둥의 특징이다.
무차원 변수 (Dimensionless Parameters)
이 응력에 대한 방정식은 무차원수로 표시할 수 있고, 단일 그래프로 일련의 무차원 변수를 사용하여 모든 해를 표시할 수 있다. 이 무차원 방정식은 위의 방정식에서 A를 좌변으로 이동하고 Pcr로 양변을 나누면 된다.
\[{\sigma_{\rm max}A\over P_{cr}}={P\over P_{cr}}\left\{1+{ecA\over I}\sec\left({\pi\over2}\sqrt{P\over P_{cr}}\right)\right\}\]
위의 방정식은 무차원이다. 이 방정식은 몇 개의 무차원항을 포함한다: (σmaxA/Pcr), (ecA/I), 및 (P/Pcr). 이제 이 방정식의 모든 해는 단일 그래프 상에 일련의 마스타-커브(master-curves)로 표시할 수 있다.
무차원 변수 계산 예제 (Dimensionless Parameter Calculation Example)
\(E=10×10^6\) psi이고 σy=65,000 psi 인 100 in 알루미늄 장주(長柱)가 있다고 한다. 장주의 C=0.5 in, A=1 in², 그리고 I=1 in⁴ 이면 Pcr은
\[P_{cr}={\pi^2EI\over L^2}={\pi^2(10\times10^6)(1)\over100^2}=9,870\ {\rm lb}\]
하지만 이제 하중이 기둥측으로부터 3 in 떨어져 있다고 가정한다. 그러면 기둥의 응력이 알루미늄의 항복강도에 도달할 것이기 때문에 Pcr 보다 작은 하중에서 붕괴될 것이다. 얼마나 낮은 하중인지 결정하기 위하여, 먼저 다음을 계산한다.
\[{\sigma_yA\over P_{cr}}={(65,000)(1)\over9,870}=6.59\]
그리고 또한 아래 계산이 필요하다.
\[{ecA\over I}={(3)(0.5)(1)\over1}=1.5\]
그러므로 y값 6.59와 편심량 1.5 곡선의 교점의 x값, P/Pcr=0.77을 찾을 수 있다. 따라서 기둥의 응력은 다음 하중일 때 σy에 도달한다.
\[P=0.77\times9,890=7,600\ {\rm lb}\]
응력을 포함하는 무차원항은 또 하나의 의미를 가진다. 이를 다시 쓰면
\[{\sigma_{\rm max}\over P_{cr}/A}={\sigma_{\rm max}\over\sigma_{cr}}={\sigma_{\rm yield}\over\sigma_{cr}}\]
위의 식은 분모는 기둥의 좌굴 임계 압축응력 σcr로 생각할 수 있다. (e=0 일 때) 또한, 앞의 예제와 같이 기둥의 최대하중 P를 구하기 위한 최대응력 σmax는 재료의 항복강도 σyield와 같다고 볼 수 있다. 따라서, σmaxA/Pcr은 임계응력(critical stress) Pcr/A에 대한 재료의 항복강도의 비(比)인 σyield/σcr로 해석될 수 있다.







댓글
댓글 쓰기