수직응력과 변형률 (Normal Stress and Strain)
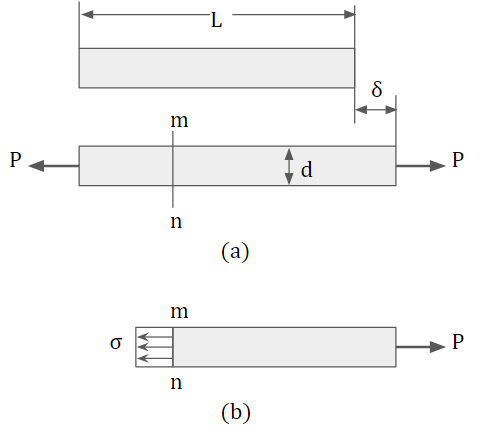 |
| 그림 1. 인장 상태의 균일단면 봉 |
축방향 힘에 의해 봉에 생성된 내부응력을 조사하기 위해 가상의 단면 mn(그림 1a)를 자른다. 이 단면은 봉의 종축(longitudinal axis)에 수직이다; 따라서 횡단면(cross section)으로 알려져 있다. 이제 절단면 오른쪽에 있는 부분을 자유체(free body)로 분리한다(그림 1b). 인장하중 P는 자유체의 오른쪽 끝단에 작용한다; 다른쪽 끝단에는 제거된 부분의 작용을 나타내는 힘들이 남아 있는 부분에 존재한다. 이 힘들은 수직단면에 걸쳐 잠겨있는 수평면에 작용하는 정수합(hydrostatic pressure)의 분포와 유사하게 연속적으로 분포한다. 이 힘의 강도(즉, 단위면적당 힘)를 응력(stress)이라고 하며 일반적으로 그리스 문자 σ(sigma)로 표시된다. 응력에 단면 전체에 걸쳐 균일한 분포를 갖는다고 가정하면(그림 1b) 합력(resultant)이 봉의 단면적 A에 강도 σ를 곱한 값과 같다는 것을 쉽게 알 수 있다. 또한 그림 1b에 표시된 물체의 평형으로부터 이 합력은 가해진 하중 P와 크기가 같고 방향이 반대임이 분명하다. 따라서 축방향으로 하중을 받는 임의의 일정한 단면 봉에서 균일한 응력에 대한 방정식을 얻는다.
\[\sigma={P\over A}\]
그림과 같이 봉이 힘 P에 의해 신장될 때, 그 결과 응력은 인장응력(tesile stress)이다; 힘의 방향이 바뀌면 봉이 압축되어 압축응력(compressive stress)이 발생한다. 이 응력들은 절단면에 수직한 방향으로 작용하기 때문에 수직응력(normal stress)이라고 한다. 따라서 수직응력은 인장 또는 압축응력일 수 있다. 나중에 표면에 평행하게 작용하는 전단응력(shear stress)이라고 하는 다른 형태의 응력을 만나게 된다.
수직응력의 부호규약(sign convention)이 요구될 때, 통상 인장응력을 양수, 압축응력은 음수로 정의 한다.
수직응력 σ는 수직력을 단면적으로 나누기 때문에 단위면적 당 힘의 단위(units)를 갖는다. SI 단위계가 사용될 때는 힘은 뉴우톤(Newtons, N), 면적은 평방미터(square meters, \({\rm m}^2\))로 표현된다. 따라서 응력은 평방미터 당 뉴우톤(\(\rm N/m^2\)) 또는 파스칼(Pa)의 단위를 가진다. 하지만 파스칼은 응력의 단위로는 작기 때문에 몇 배 큰 단위로 작업이 필요하다. 이 점을 설명하기 위해 1 psi를 만들기 위해서는 거의 7,000 Pa를 취해야 한다는 점에 주의해야 한다. 예를 들면, 강재 봉(steel bar)는 보통 인장응력으로 \(140\times10^6\) Pa인 140 MPa를 가질 수 있다. 편리하게 쓸 수 있는 다른 단위로는 kPa과 GPa이 있다; 전자는 \(10^3\)Pa, 그리고 후자는 \(10^6\)Pa과 같다. SI에서는 비추천하지만 때때로 MPa과 동일한 단위인 평방 밀리미터 당 뉴우톤(\(\rm N/mm^2\))으로 주어진 응력도 찾을 수 있다.
USCS 단위계를 사용할 때는 응력은 통상 평방인치 당 파운드(psi) 또는 킵스(kips, or kilopound=1,000 lb) 당 평방인치(ksi)로 표현된다. 예를 들면, 강재 봉의 일반적인 응력은 20,000 psi 또는 20ksi 일 수 있다.
방정식 σ=P/A이 유효하기 위해서는 응력 σ가 횡단면에 걸쳐서 균일하게 분포되어야만 한다. 이 조건은 축하중 P가 예제 1과 같이 도심(centroid)에 작용하면 성립한다. 하중 P가 도심에 작용하지 않을 때는 봉의 굽힘(bending)이 발생하고 더 복잡한 분석이 필요하다. 하지만 여기서는 별도로 명기하지 않는 한 모든 축 하중은 도심을 통과하는 것으로 간주한다.
그림 1b에 도시된 균일 응력 조건은 끝단을 제외한 부재의 길이를 따라 존재한다. 봉의 끝단의 응력분포는 축하중 P가 실제로 어떻게 적용되는지에 따라 다르게 된다. 만약 하중 자체가 균일하게 끝단에 분포된다면 끝단의 응력양상도 다른 곳과 동일할 것이다. 하지만 보통 국소적으로 집중되어 있고, 결과적으로 높은 국부 응력과 단면에 걸쳐 불균일한 응력분포를 나타낸다. 끝단에서 멀리 떨어질 때 응력분포는 점진적으로 그림 1b와 같이 균일한 분포에 접근하게 된다. 공식 σ=P/A가 양호한 정확도로 사용되려면 보통 끝단에서 최소한 거리 d 이상 떨어진 점이 안전하다. 여기서 d는 봉재의 가장 큰 횡방향 치수이다(그림 1a 참조). 물론 응력이 불균일 한 경우도 방정식 σ=P/A는 평균 수직응력(average normal stress)을 줄 것이다.
축방향 하중을 받는 봉재는 인장일 때 길어지고, 압축일 때 짧아지는 길이의 변화를 겪게 된다. 전체 길이의 변화를 그리스 문자 δ(delta)로 표시하고 그림 1a 인장을 받는 봉에 도시하였다. 이 늘음(elongation)은 봉의 길이 L에 걸쳐서 재료 신장의 누적된 결과이다. 이제 봉의 모든 곳에서 재료가 동일하다고 가정하자. 그 다음 봉의 반쪽을 생각하면 늘음은 δ/2와 같을 것이다; 유사하게 봉의 단위 길이를 고려하면 그것은 전체 늘음 δ의 1/L 배와 같을 것이다. 이와 같이 단위 길이 당 늘음, 또는 그리스 문자 ε으로 표기되고 다음식으로 주어지는 변형률(strain)의 개념에 도달하게 된다.
\[\epsilon={\delta\over L}\]
봉이 인장상태이면, 변형률은 재료의 늘음 또는 신장을 나타내는 인장변형률(tensile strain)로 불리운다. 봉이 압축상태이면, 변형률은 압축변형률(compressive strain)이고 봉은 단축된다. 인장변형률은 양수, 압축변형률은 음수를 취한다. 이 변형률 ε은 수직응력에 관련이 있으므로 수직변형률(normal strain)로 불리운다.
수직변형률 ε은 두 길이의 비이므로 무차원양(dimensionless quantity)이다; 즉, 단위가 없다. 이렇게 변형률은 어느 단위계에도 의존하지 않는 순수한 숫자로 표현된다. 변형률의 수치는 특히 통상적으로 치수의 미소한 변화만을 겪는 구조용 재질의 경우 매우 작은 것이 보통이다. 요컨데, 2.0m 길이의 강재 봉을 생각하자. 인장하중을 받을 때 1.4mm의 양만큼 늘어날 수 있다. 이에 해당하는 변형률은
\[\epsilon={\epsilon\over L}={\rm1.4\times10^{-3}m\over2.0m}=0.0007=700\times10^{-6}\]
이다. 실제로는 δ 및 L의 원래 단위를 변형률 자체에 붙여쓰기도 하는데, 이 경우 변형률은 mm/m, μm/m, 및 in./in. 와 같이 기록된다. 예를 들면, 앞의 설명에서 변형률 ε은 700 μm/m 또는 \(\rm700\times10^{-6}in./in.\)와 같이 주어질 수 있다.
수직응력과 변형률의 정의는 정적(static)이고 기하학적 고려에 기반한 것으로 앞의 두 정의식은 임의의 하중 크기와 재질에 사용될 수 있다. 주요 요구사항은 봉의 변형은 균일해야 된다는 것으로, 바꿔말하면 균일 단면(prismatic) 봉이고 단면의 도심에 하중이 작용하며 균질체(homogeneous) 재질(즉, 봉의 모든 부분이 동일)이어야 한다. 이 결과 응력과 변형률의 상태를 단축응력과 변형률(uniaxial stress and strain)이라 칭한다. 봉의 종방향 이외의 단축응력도 있으며 이축응력(biaxial stress) 및 평면응력(plane stress)과 같은 더 복잡한 응력상태도 있다.
예제 1
일정한 단면 부재에 균일한 인장 또는 압축을 발생시키는 축하중 P는 반드시 횡단면의 도심에 작용해야함을 보여라.
 |
| 그림 2. 예제 1. 단면의 도심에 작용하는 축하중 P |
그림 2a와 같이 단면은 임의의 형상을 가지고 단면 평면에 임의의 xy축을 취한다. 그러면 봉의 길이 방향은 z축이 된다(그림 2b). 단면에 걸친 응력분포는 그림 2b와 같이 균일한 인장응력 σ=P/A로 가정한다. 이 응력분포의 합력은 축하중 P 이다.
힘 P의 작용선의 x와 y 좌표는 그림에서 \(\rm x_c\ y_c\)로 표시한다. 이 좌표들을 결정하기 위해 힘 P의 x와 y축에 관한 모멘트 \(\rm M_x\)와 \(\rm M_y\)는 각각 균일 분포된 해당 응력의 모멘트와 같아야 한다. 힘 P에 의한 모멘트들은 \(\rm M_x=Py_c,\,M_y=-Px_c\) 이고 여기서 모멘트는 (오른손 법칙을 사용하여) 그 벡터가 축의 양의 방향으로 작용할 때 양수로 생각한다. 분포 응력의 모멘트를 얻기 위해 단면 내의 면적요소 dA를 생각하면(그림 2a) 이 요소에 작용하는 미소 힘은 σdA 이다. 이 요소 힘의 x와 y축에 관한 모멘트는 각각 σydA 및 -σxdA 이며 여기서 x와 y는 요소 dA의 좌표를 나타낸다. 전체 모멘트는 전체 단면적 A에 걸쳐 적분하면 얻을 수 있다; 이렇게 x와 y축에 관한 모멘트는 \(\rm M_x=\int\sigma ydA,\,M_y=-\int\sigma ydA\) 이다. 이들은 P에 의한 모멘트와 동일하므로:
\[M_x=Py_c=\int\sigma ydA\qquad M_y=Px_c=\int\sigma xdA\]
힘 P와 σA는 같다는 것과 응력 σ는 일정하다는 것에 주의하면 앞의 방정식으로부터 \(\rm y_c\)와 \(\rm x_c\)에 대한 다음 공식을 얻는다:
\[y_c=\frac{\int ydA}{A}\qquad x_c=\frac{\int xdA}{A}\]
이 방정식들은 합력 P의 작용선 좌표가 단면적의 1차 모멘트를 그 면적 자신으로 나눈 것과 같음을 보여준다. 이렇게 이 방정식들은 면적의 도심 좌표를 정의하는 방정식들과 동일하다.
따라서 중요한 일반적 결론에 도달하였다. 균일단면 봉에서 균일한 인장 또는 압축을 얻기 위해서는 축방향 힘은 반드시 단면적의 도심을 통과하여 작용해야 한다.
예제 2
사각단면 (20×40mm) 및 길이 L=2.8m의 균일단면 봉이 축방향 인장력 70kN을 받고 있다(그림 3). 계측된 봉의 늘음이 δ=1.2mm 이다. 봉의 인장응력과 변형률을 계산하여라.
 |
| 그림 3. 예제 2. 사각형 균일단면봉 |
축방향 힘은 끝단면의 도심에 작용한다고 가정하면 응력의 정의식을 이용할 수 있다.
\[\sigma={P\over A}={\rm70\ kN\over(20\ mm)(40\ mm)}=87.5\ \rm MPa\]
또한 변형률의 정의식으로부터
\[\epsilon={\delta\over L}={\rm1.2\ mm\over2.8 m}=429\times10^{-6}\]
이 σ와 ε값들이 각각 종의 종방향 인장응력과 변형률을 나타낸다.
예제 3
심정(Deep-well) 펌프가 피스톤을 상하로 움직이는 크랭크에 의해 가동되고 있다. 펌프 로드의 직경은 d=0.6 in. 이고 길이는 L=320 ft. 이다. 이것은 비중량 γ=490 lb/ft³의 강재로 만들어 졌다. 피스통에 걸리는 저항은 하방행정(downstroke) 동안에 200 lb 이고 상방행정(upstroke)일 동안에는 2000 lb 이다. 펌프 로드의 최대 인장 및 압축응력을 저항력과 로드의 비중량만을 고려하여 결정하라.
 |
| 그림 4. 예제 3. 심정(Deep-well) 펌프 로드 |
하방행정 동안에 피스톤의 저항은 로드의 길이에 걸쳐 압축력 C=200 lb를 발생시키고, 상방행정 동안에는 인장력 T=2000 lb를 발생시틴다. 로드의 중량은 하단의 영으로부터 상단에서 최대 인장력을 유발한다. 이 최대 중량은 다음식으로 주어지는 무게와 동일하고 상단에서 인장력으로 작용한다.
\[W=\gamma LA=\rm(490\ lb/ft^3)(320\ ft)\left({\pi\over4}\right)\left({0.6\ in.\over12\ in./ft}\right)^2=308\ lb\]
상방행정 동안에 펌프 로드 상단에서 T+W, 또는 2308 lb의 최대 인장력이 발생한다. 이에 해당하는 최대 인장응력은
\[\sigma_t={P\over A}=\rm{2308\ lb\over\pi(0.6\ in.)^2/4}=8160\ psi\]
이다. 유사한 방법으로 하방행정 동안 하단에서 발생하는 최대 압축응력을 계산할 수 있다.
\[\sigma_c={P\over A}=\rm{200\ lb\over\pi(0.6\ in.)^2/4}=710\ psi\]
이 계산들은 단지 특정 하중에 의한 펌프 로드의 축방향 응력을 준다. 펌프 로드의 굽힘 및 동적 효과와 같은 기타 사항은 고려되지 않았다.



댓글
댓글 쓰기