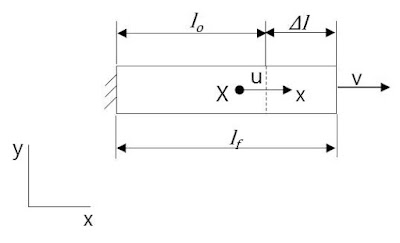
유체에 잠겨 있는 물체에 작용하는 힘
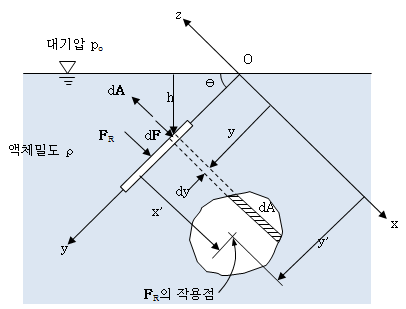
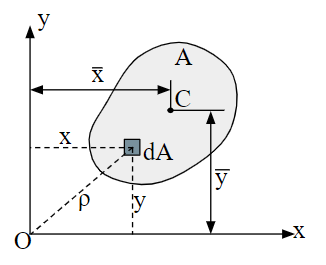
정지유체에서는 높이에 따라 압력 이 변화한다. 이러한 압력이 액체 내에 잠겨 있는 물체에 대한 표면력으로서 어떻게 작용하는지 알아본다. 물체표면에 작용하는 힘을 결정하기 위해서는 아래의 사항들을 알아야 한다. 1) 힘의 크기 2) 힘의 방향 3) 합력(合力, resultant force)의 작용선 잠겨 있는 평판에 작용하는 힘 잠겨 있는 평판에 작용하는 압력의 합력을 계산하기 위해서 아래 그림처럼 좌표계를 설정하고 평판의 평면이 xy 좌표평면에 놓이도록 한다. 유체에 잠겨진 평판 정지유체내에서는 전단응력 이 작용하지 않기 때문에 표면에 위치한 임의의 미소요소에 작용하는 힘은 그 표면에 대해서 수직하게 작용하게 된다. 윗쪽 면의 미소면적 dA에 작용하는 합력은 d F =-pd A 로 주어진다. 벡터 d A 의 양(+)의 방향을 도시된 면적의 바깥 쪽으로 수직하게 선정하였기 때문에 앞 식의 (-)부호는 힘 d F 가 면적요소의 방향에 대해 반대방향으로 작용함을 나타낸다. 표면에 작용하는 합력은 일반적으로 다음과 같이 나타낼 수 있다. \(\begin{align}{\bf F}_R=\int_Ad{\bf F}=\int_A-pd{\bf A}\cdot\cdot\cdot(1)\end{align}\) 식 (1)의 적분값을 계산하기 위해서는 압력 p와 면적벡터 d A 가 모두 같은 변수의 항으로 표시되어야만 한다. 밀도 가 일정한 유체의 경우 깊이 h인 곳의 압력 p는 \(p=p_o+\rho gh\) 이므로 이것을 \(h=y\sin\theta\)의 관계식과 함께 식 (1)에 대입하면 합력 \(F_R\)은 다음과 같이 적분될 수 있다. \(\begin{align}F_R&=|{\bf F}_R|=p_oA+\rho \sin\theta\int_AydA\\&=\left(p_o+\rho g\sin\theta y_c\right)A=p_cA\end{align}\) 여기서 도심(centroid) 까지의 길이 \(y_c\)는 그 정의에 의해 \(y_cA=\int_Ayd...