진변형률 (True Strain)

진변형률(true strain) \(\epsilon\)은 물체의 인장/압축 조건에서 다음과 같이 정의한다.

\(\epsilon=\ln\left(\dfrac{l_f}{l_o}\right)\)

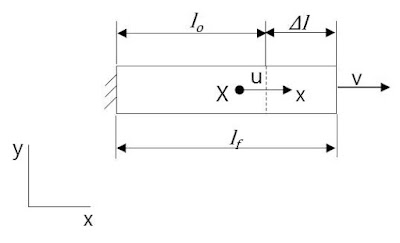
여기서 \(l_o\)는 변형전, \(l_f\)는 변형후 길이이다.

변형률속도와 진변형률의 관계를 다음 예제를 통하여 알아본다. 초기 0.5m의 물체가 v의 속도로 인장하여 2s 후 0.55m로 되었다면 6s 후 진변형률을 구해본다. 진변형률은 변형률속도의 시간적분으로 구할 수 있다. 먼저, 변형률속도와 시간증분의 곱은 \({\rm D}dt=\dfrac{\partial v}{\partial x}=\dfrac{\partial\dot{u}}{\partial x}dt=\dfrac{\partial}{\partial x}\left(\dfrac{du}{dt}\right)dt=\dfrac{dl}{l}\) 진변형률은 이를 적분하면 되므로 \(\begin{split}\epsilon=\int_0^6{\rm D}dt=\int_0^6\dfrac{dl}{l}=\ln\left(\dfrac{l_f}{l_o}\right)=\ln\left({0.65\over 0.50}\right)=0.262\end{split}\) 여기서 \(l_f=0.65\)는 다음식으로 구한다. \(v=\dfrac{\Delta L}{\Delta t}=\dfrac{0.05}{2}=0.025,\ l_f=l_o\left(1+\dfrac{vt}{l_o}\right)=0.5\left(1+\dfrac{(0.025)(6)}{0.50}\right)=0.65\) 위와 같이 변형률속도의 시간적분으로 진변형률을 구할 경우 강체회전은 무시되어야 한다.

진변형률과 공학변형률(engineering strain)의 관계

진변형률 \(\epsilon\)과 공학변형률 \(\epsilon_{\rm Eng}\)의 관계는 다음과 같이 유도된다.

\(\epsilon=\ln\left(\dfrac{l_f}{l_o}\right)=\ln\left(\dfrac{l_o+\Delta l}{l_o}\right)=\ln\left(1+\dfrac{\Delta l}{l_o}\right)=\ln(1+\epsilon_{\rm Eng})\)

진변형률과 비압축성 재료(incompressible material)

비압축성 재료에서 체적 불변이므로 진변형률은 다음과 같은 조건을 가진다.

초기와 최종 체적의 비는

\(\dfrac{{\rm V}_f}{{\rm V}_o}=\left(\dfrac{{\rm W}_f}{{\rm W}_o}\right)\left(\dfrac{{\rm D}_f}{{\rm D}_o}\right)\left(\dfrac{{\rm H}_f}{{\rm H}_o}\right)=1\)

양변에 로그를 취하면 진변형률의 대각합(trace)은

\(\ln\left(\dfrac{{\rm W}_f}{{\rm W}_o}\right)\ln\left(\dfrac{{\rm D}_f}{{\rm D}_o}\right)\ln\left(\dfrac{{\rm H}_f}{{\rm H}_o}\right)=\epsilon_1+\epsilon_2+\epsilon_3={\rm tr}(\epsilon)\)

변형률속도 대각합도 또한

\({\rm tr}(\dot{\epsilon})=\dot{\epsilon}_1+\dot{\epsilon}_2+\dot{\epsilon}_3=\rm tr(D)=D_{11}+D_{22}+D_{33}=0\)

진변형률과 회전

강체 회전이 있을 때는 진변형률을 구하기 위한 변형률 속도의 시간 적분에 회전 변환을 고려한다.

\(\begin{align}\epsilon=\int {\bf R}^T{\bf DR}dt\end{align}\)

다음 예제는 초기 정사각형이 인장과 동시에 회전을 하는 경우이며 90˚, 0.2s 시점까지 변형한다. 2-D이므로 회전 행열 R은

\({\bf R}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix},\ {\bf R}^T=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\)

t=0 에서 x방향 인장과 동시에 y 방향은 포아송 효과(Poisson's effect)로 수축한다. 따라서 변형률속도 텐서를 아래와 같이 가정하면 \(\Delta t=0.1\) 동안 진변형률 증분은

\({\bf D}=\begin{bmatrix}3.0&0.0\\0.0&-2.0\end{bmatrix},\ {\bf R}=\begin{bmatrix}1&0\\0&1\end{bmatrix},\ \Delta\epsilon={\bf R}^T{\bf DR}(\Delta t)=\begin{bmatrix}0.3&0.0\\0.0&-0.2\end{bmatrix}\)

이후 45˚ 회전 시 순수전단 상태가 되므로 변형률속도 텐서를 아래와 같이 가정하면 진변형률 증분은

\({\bf D}=\begin{bmatrix}0.0&1.5\\1.5&0.0\end{bmatrix},\ {\bf R}=\begin{bmatrix}0.7071&-0.7071\\0.7071&0.7071\end{bmatrix},\ \Delta\epsilon={\bf R}^T{\bf DR}(\Delta t)=\begin{bmatrix}0.15&0.0\\0.0&-0.15\end{bmatrix}\)

마지막 90˚ 회전 시점에서는 y방향 인장, x방향 수축이므로 가정된 변형률속도 텐서의 진변형률 증분은

\({\bf D}=\begin{bmatrix}-1.0&0.0\\0.0&1.5\end{bmatrix},\ {\bf R}=\begin{bmatrix}0&-1\\1&0\end{bmatrix},\ \Delta\epsilon={\bf R}^T{\bf DR}(\Delta t)=\begin{bmatrix}0.15&0.0\\0.0&-0.10\end{bmatrix}\)

최종적으로 전체 진변형률은 각 증분을 더하여 계산된다.

\(\begin{align}\epsilon=\int {\bf R}^T{\bf DR}dt=\sum\Delta\epsilon=\begin{bmatrix}0.60&0.00\\0.00&-0.45\end{bmatrix}\end{align}\) 

[예제] 평면변형률이 다음과 같이 정의될 때 (x, y) 점의 각 방향별 변위와 전단변형률 \(\gamma_{xy}\)를 구하여라. 단, 강체 회전은 일어나지 않는다. \(\begin{split}\epsilon_x&=-3x^2+7y^2\\\epsilon_y&=x^2-5y^2\end{split}\) <풀이> x, y 방향 변위를 각각 u, v라 하면 각 방향별 변형률을 원점에서 해당 지점까지 적분하여 구한다. \(\begin{split}u&=\int_0^x\epsilon_xdx=\int_0^x\left(-3x^2+7y^2\right)dx=-x^3+7xy^2\\v&=\int_0^y\epsilon_ydy=\int_0^y\left(x^2-5y^2\right)dy=x^2y-{5\over 3}y^3\end{split}\) 전단변형률은 정의에 따라 위의 변위식을 미분하여 구한다. \(\gamma_{xy}=2\epsilon_{xy}=\dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x}=2xy+14xy=16xy\)

출처 : www.continuummechanics.org