유체에 잠겨 있는 물체에 작용하는 힘

정지유체에서는 높이에 따라 압력이 변화한다. 이러한 압력이 액체내에 잠겨 있는 물체에 대한 표면력으로서 어떻게 작용하는지 알아본다. 물체표면에 작용하는 힘을 결정하기 위해서는 아래의 사항들을 알아야 한다.

1) 힘의 크기

2) 힘의 방향

3) 합력(合力, resultant force)의 작용선

잠겨 있는 평판에 작용하는 힘

잠겨 있는 평판에 작용하는 압력의 합력을 계산하기 위해서 아래 그림처럼 좌표계를 설정하고 평판의 평면이 xy 좌표평면에 놓이도록 한다.

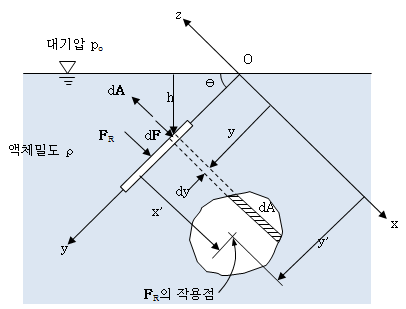유체에 잠겨진 평판

정지유체내에서는 전단응력이 작용하지 않기 때문에 표면에 위치한 임의의 미소요소에 작용하는 힘은 그 표면에 대해서 수직하게 작용하게 된다. 윗쪽 면의 미소면적 dA에 작용하는 합력은 dF=-pdA로 주어진다.

벡터 dA의 양(+)의 방향을 도시된 면적의 바깥 쪽으로 수직하게 선정하였기 때문에 앞 식의 (-)부호는 힘 dF가 면적요소의 방향에 대해 반대방향으로 작용함을 나타낸다. 표면에 작용하는 합력은 일반적으로 다음과 같이 나타낼 수 있다.

\(\begin{align}{\bf F}_R=\int_Ad{\bf F}=\int_A-pd{\bf A}\cdot\cdot\cdot(1)\end{align}\)

식 (1)의 적분값을 계산하기 위해서는 압력 p와 면적벡터 dA가 모두 같은 변수의 항으로 표시되어야만 한다.

밀도가 일정한 유체의 경우 깊이 h인 곳의 압력 p는 \(p=p_o+\rho gh\) 이므로 이것을 \(h=y\sin\theta\)의 관계식과 함께 식 (1)에 대입하면 합력 \(F_R\)은 다음과 같이 적분될 수 있다.

\(\begin{align}F_R&=|{\bf F}_R|=p_oA+\rho \sin\theta\int_AydA\\&=\left(p_o+\rho g\sin\theta y_c\right)A=p_cA\end{align}\)

여기서 도심(centroid)까지의 길이 \(y_c\)는 그 정의에 의해 \(y_cA=\int_AydA\) 이고 \(p_c\)는 그 도심에 작용하는 압력이 된다. 즉, 비압축성유체속에 잠겨있는 평판에 작용하는 합력은 그 평판의 도심에 작용하는 압력과 평판의 면적을 곱한 것과 같다.

합력의 어떤 임의의 축에 대한 모멘트(moment)는 그 축에 대한 분포된 힘들의 모멘트의 합과 같으므로, 이것을 이용하면 합력의 작용점을 찾을 수 있다. 좌표계의 원점으로부터 합력이 작용하는 점까지의 위치 벡터를 r'로 표시하면

\(\begin{align}{\bf r}'\times{\bf F}_R=\int {\bf r}\times d{\bf F}=\int_A{\bf r}\times pd{\bf A}\cdot\cdot\cdot(2)\end{align}\)

위의 그림에서 보는 바와 같이 r'=ix'+jy', 그리고 r'=ix+jy 이며 dA=dAk 임을 알 수 있다. 합력 \({\bf F}_R\)은 표면 dA의 방향에 대해 반대 방향으로 작용하므로 \({\bf F}_R=-F_R{\bf k}\) 이다. 이들 값들을 식 (2)에 대입하면

\(\begin{align}({\bf i}x'+{\bf j}y')\times-F_R{\bf k}=\int({\bf i}x+{\bf j}y)\times d{\bf F}=-\int_A({\bf i}x+{\bf j}y)\times pdA{\bf k}\end{align}\)

그러므로

\(\begin{align}({\bf j}x'-{\bf i}y')F_R=\int_A({\bf j}x-{\bf i}y)\end{align}\)

이것은 벡터표현이므로, 각 성분별로 분해하면

\(\begin{split}x'F_R=\int_AxpdA\\y'F_R=\int_AypdA\end{split}\)

여기에서 x'와 y'는 합력이 작용하는 점의 좌표이다. 식 (1)과 (2)는 잠겨있는 평면에 작용하는 힘의 크기와 그 힘의 작용점을 결정하는데 이용될 수 있다. 이들 식은 밀도가 상수이어야 한다거나, 액체의 표면상태가 대기압이어야 한다는 조건들을 포함하지 않는다.

[예제 1] 폭이 5m 이고 A 점이 힌지(hinge)된 경사면이 그림과 같은 상태에 있다. 경사면에 작용하는 합력 \({\bf F}_R\)을 결정하여라.

<풀이> 폭을 w라 하면 dA=wdyk 이고 비압축성유체에서는 ρ=일정이므로

\(p=\rho gh=\rho g(D+y\sin30^\circ)\)

을 이용해 합력을 구할 수 있다.

\(\begin{align}{\bf F}_R&=-\int_Apd{\bf A}=-\int_0^L\rho g(D+y\sin30^\circ)wdy{\bf k}\\&=-\rho gw\left(DL+{L^2\over 4}\right)=-999\times9.81\times5\left(2\times4+{4^2\over4}\right){\bf k}\\&=-588{\bf k}\ {\rm kN}\end{align}\)

합력의 작용선 x', y'은

\(\begin{split}x'&={1\over F_R}\int_AxpdA={1\over F_R}\int_0^L\int_0^wxpdxdy={w\over2F_R}\int_0^Lpwdy={w\over2}=2.5{\rm m}\\y'&={1\over F_R}\int_AypdA={1\over F_R}\int_0^Lypwdy=\frac{\rho gw}{F_R}\int_0^L(D+y\sin30^\circ)ydy\\&=\frac{\rho gw}{F_R}\left(\frac{DL^2}{2}+\frac{L^3}{6}\right)=\frac{999\times9.81\times5}{588\times10^3}\left(\frac{2\times4^2}{2}+\frac{4^3}{6}\right)=2.22{\rm m}\end{split}\)

따라서, r'=2.5i+2.22j m 이다.

[예제 2] 그림과 같이 폭 5ft, 길이 AB가 10ft인 구형문(矩形門)이 B점에서 힌지(hinge)되어 있다. 문의 무게는 무시하고 정지점 A에 작용하는 단위길이당의 힘을 구하라.

<풀이> 압력-높이의 기본식에서 γ=상수라고 가정하면

\(p=\gamma h=\gamma(D+y\sin30^\circ)\)

평형상태에서는 ∑M=0 이기 때문에 다음과 같이 쓸 수 있다.

\(\begin{align}F_AL=\int(L-y)dF=\int_A(L-y)pdA=\int_0^L(L-y)pwdy=w\gamma\int_0^L(L-y)(D+y\sin30^\circ)dy\end{align}\)

또는

\(\begin{split}{F_A\over w}&={\gamma\over L}\int_0^L\left(DL+Ly\sin30^\circ-Dy-y^2\sin30^\circ\right)dy\\&={\gamma\over L}\left(\frac{DL^2}{2}+\frac{L^3}{12}\right)={62.4\over10}\left(\frac{5\times10^2}{2}+\frac{10^3}{12}\right)=2,080\,{\rm lbf/ft}\end{split}\)

정지점에 작용하는 힘은 z 축의 음의 방향으로 작용하므로 -2,080k lbf/ft 이다.

잠겨 있는 곡면에 작용하는 힘

곡면의 미소요소 dA에 작용하는 힘은 표면에 수직하게 작용하기는 하지만 표면의 곡률 때문에 위치에 따라 서로 다른 방향으로 작용하게 된다. 각기 다른 방향으로 작용하는 힘들의 합을 구하기 위해서 보통 많이 이용하는 방법은 직교좌표계에서 벡터성분들의 합을 구하는 것이다. 이를 위해 그림에 나타나 있는 곡면을 고려해 보자.

유체에 잠긴 곡면

미소면적요소 dA에 작용하는 압력의 합력은

\(d{\bf F}=-pd{\bf A}=dF_x{\bf i}+dF_y{\bf j}+dF_z{\bf k}\)

이다. 또 전면적에 작용하는 압력의 합력을 성분별로 나타내면

\(\begin{align}{\bf F}_R=-\int_Apd{\bf A}={\bf i}F_{Rx}+{\bf j}F_{Ry}+{\bf k}F_{Rz}\end{align}\)

으로 쓸 수 있고, 여기서 \(F_{Rx},\,F_{Ry},\,F_{Rz}\)는 각각 x, y, z의 양의 방향으로의 합력 벡터 성분(resultant vector components)이다.

힘의 성분들을 구하기 위해서, 단위벡터(unit vector)와 윗 식으로 주어지는 힘벡터의 내적(dot product)를 취한다. 그러면 다음 식들을 얻는다.

\(\begin{align}F_{Rx}&=\int dF_x={\bf F}_R\cdot{\bf i}=\int d{\bf F}\cdot{\bf i}=-\int_Apd{\bf A}\cdot{\bf i}=-\int_ApdA\cos\theta_x=\pm\int_{A_x}pdA_x\\F_{Ry}&=\int dF_y={\bf F}_R\cdot{\bf j}=\int d{\bf F}\cdot{\bf j}=-\int_Apd{\bf A}\cdot{\bf j}=-\int_ApdA\cos\theta_y=\pm\int_{A_y}pdA_y\cdot\cdot\cdot(3)\\F_{Rz}&=\int dF_z={\bf F}_R\cdot{\bf k}=\int d{\bf F}\cdot{\bf k}=-\int_Apd{\bf A}\cdot{\bf k}=-\int_ApdA\cos\theta_z=\pm\int_{A_z}pdA_z\end{align}\)

여기에서 \(\theta_x\)는 dA와 단위벡터 i 사이의 각이고, \(\theta_y\)는 dA와 단위벡터 j 사이의 각이며, \(\theta_z\)는 dA와 단위벡터 k 사이의 각이다. 또한 미소면적들은 다음과 같다.

\(dA_x=dA\cos\theta_x\)는 x 축에 수직인 면에 대한 면적요소 dA의 투영면적

\(dA_y=dA\cos\theta_y\)는 y 축에 수직인 면에 대한 면적요소 dA의 투영면적

\(dA_z=dA\cos\theta_z\)는 z 축에 수직인 면에 대한 면적요소 dA의 투영면적

식 (3)의 마지막 항에서 부호(+ 또는 -)는 벡터 dA와 단위벡터 사이의 각의 크기에 따라 변한다. 식 (3)에서 계산된 힘의 성분이 음의 값을 갖으면, 힘은 좌표축의 음의 방향으로 작용한다.

잠겨진 물체의 곡면에 작용하는 합력을 결정하려면 합력의 각 성분의 크기를 계산하여야 한다. 평면에 작용하는 힘을 구했을 때처럼 식 (3)의 적분은 압력 p와 면적요소 dA를 같은 변수로 표현한 다음에 수행하여야 한다.

합력의 연직방향 성분 \(F_{Rz}\)를 고려함에 있어 액체만에 의해 작용하는 압력은

\(\begin{align}p=\int_{z_s}^{z_0}\rho gdz\end{align}\)

으로 표시할 수 있다. 여기서 \(z_s\)는 고려하는 면의 연직방향 좌표이고, \(z_0\)는 자유표면의 연직방향 좌표이다. 따라서 식 (3)의 마지막 성분은 다음과 같이 쓸 수 있다.

\(\begin{align}F_{Rz}=\pm\int_{A_z}pdA_z=\pm\int_{A_z}\left(\int_{z_s}^{z_0}\rho gdz\right)dA_z\end{align}\)

위 식 중 \(\left(\int_{z_s}^{z_0}\rho gdz\right)dA_z\)는 미소면적요소 \(dA_z\) 위의 액체기둥(곡면에서부터 자유표면까지)의 무게를 표시한다. 따라서 액체에 의한 합력의 연직방향성분은 윗 식에서와 같이 그 곡면 윗부분에 있는 액체의 전체 무게와 같다.

합력의 수평방향 성분 \(F_{Rx}\)와 \(F_{Ry}\)는 식 (3)의 첫번째와 두번째 성분으로부터 곡면을 각각 x 축 및 y 축에 수직한 면에, 위의 그림에서 보는 바와 같이, 투영한 면적 OBC와 면적 OAC에 작용하는 힘과 같음을 알 수 있다. 왜냐하면 곡면상의 미소면적 dA에 작용하는 압력과 dA를 수평하게 투영한 미소면적 \(dA_x\) 및 \(dA_y\)에 작용하는 압력은 동일하기 때문이다.

합력의 각 성분의 작용선은 "어떤 주어진 축에 대해서, 합력에 의한 모멘트는 그 축에 대한 분포된 힘들에 의한 모멘트의 합과 같다"는 사실을 이용하여 찾을 수 있다. 곡면부에 작용하는 각 성분력의 작용선을 찾기 위해서 다음과 같이 쓸 수 있다.

\(\begin{split}{\bf r}_x'\times{\bf i}F_{Rx}&=\int{\bf r}_x\times dF_x{\bf i}\\{\bf r}_y'\times{\bf j}F_{Ry}&=\int{\bf r}_y\times dF_y{\bf j}\cdot\cdot\cdot(4)\\{\bf r}_z'\times{\bf k}F_{Rz}&=\int{\bf r}_z\times dF_z{\bf k}\end{split}\)

여기서 \({\bf r}_x',\,{\bf r}_y',\,{\bf r}_z'\)은 각각 x, y, z 방향의 합력성분이 작용하는 선까지의 위치벡터이다. 합력의 성분들 \(dF_x,\,dF_y,\,dF_z\)에 관한 표현은 식 (3)에 나타나 있다.

식 (3)과 (4)의 이해를 돕고자, 아래 그림에 보인 것처럼 x방향으로 일정한 폭을 갖는 면적요소 dA의 곡면을 고려하자.

유체에 잠겨있는 2차원 곡면

합력의 y, z 방향으로의 성분들은 다음과 같다.

\(\begin{split}F_{Ry}&=\int dF_y=-\int pd{\bf A}\cdot{\bf j}=-\int pdA\cos\theta_y=\ \ \ \int pdA\cos\beta=\ \ \ \int pdA_y\\F_{Rz}&=\int dF_z=-\int pd{\bf A}\cdot{\bf k}=-\int pdA\cos\theta_z=-\int pdA\sin\beta=-\int pdA_z\end{split}\)

합력 \(F_R\)의 z방향 성분의 크기는 \(\int pdA_z\)와 같고 음의 z방향으로 작용한다.

각 성분력의 작용선을 찾기 위해 다음과 같이 쓸 수 있다.

\(\begin{split}&y'{\bf j}\times F_{Rz}{\bf k}=\int y{\bf j}\times dF_z{\bf k}=\int y{\bf j}\times\left(-pdA_z{\bf k}\right)\\&z'{\bf k}\times F_{Ry}{\bf j}=\int z{\bf k}\times dF_y{\bf j}=\int z{\bf k}\times pdA_y{\bf j}\end{split}\)

이들 두 식으로부터 다음을 얻을 수 있다.

\(\begin{align}&y'=-{1\over F_{Rz}}\int_{A_z}ypdA_z\\&z'=\ \ \ {1\over F_{Ry}}\int_{A_y}zpdA_y\end{align}\)

여기서 z' 는 곡면을 y 축에 수직한 면에 투영한 면적에 작용하는 합력의 작용점과 같다는 것을 의미한다. 한편 y' 는 그 곡면위에 있는 유체의 질량중심 y 좌표와 동일함을 나타낸다.

힘의 각 성분들과 그들의 작용선들을 결정함에 있어서 평판의 경우에 했던 것과 마찬가지로, 힘의 각 성분에 대해 따로따로 기술했다. 곡면의 경우를 다루고 있기 때문에 합력의 각 성분들의 작용선이 항상 일치한다고 볼 수는 없다. 즉, 완전한 합력은 힘과 모멘트의 합으로써 나타난다.

[예제 3]  a가 4m 일 때, 표면식이 \(x=y^2/a\)로 표시되며 폭 5m로 일정한 곡면형의 문이 있다. 그림에서 보는 바와 같이 문의 오른쪽에서 물의 깊이는 4m 이다. 물 때문에 생기는 합력의 성분 \(F_{Rx}\)와 \(F_{Ry}\) 및 각 힘의 작용선을 구하라.

<풀이> 합력을 구하는 기본식을 적분하기 위하여, x 및 y의 함수로 표현된 압력 p는 다음과 같다.

\(p=\rho gh=\rho g(D-y)=\rho g(D-\sqrt{ax})\)

p에 대한 이들 값들을 \(F_{Rx},\,F_{Ry}\)의 표현식에 대입하면 다음을 얻는다.

\(\begin{align}F_{Rx}&=-\int_{A_x}pdA_x=-\int_0^Dpwdy=-\rho gw\int_0^D(D-y)dy\\&=-\frac{\rho gwD^2}{2}=-\frac{999\times9.81\times5\times4^2}{2}=-392\,{\rm kN}\\F_{Ry}&=\int_{A_y}pdA_y=\int_0^{D^2\over a}pwdx=\rho gw\int_0^{D^2\over a}(D-\sqrt{ax})dx\\&=\frac{\rho gwD^3}{3a}=\frac{999\times9.81\times5\times4^3}{3\times4}=261\,{\rm kN}\end{align}\)

\(F_{Rx},\,F_{Ry}\)의 작용선을 찾기 위해 식 (4)를 이용한다.

\(\begin{split}x'&={1\over F_{Ry}}\int_{A_y}xpdA_y={1\over F_{Ry}}\int_0^{D^2\over a}xpwdx=\frac{\rho gw}{F_{Ry}}\int_0^{D^2\over a}x(D-\sqrt{ax})dx\\&=\frac{\rho gwD^5}{10a^2F_{Ry}}=\frac{\rho gwD^5}{10a^2F_{Ry}}=\frac{\rho gwD^5}{10a^2}\left(\frac{3a}{\rho gwD^3}\right)=\frac{3D^2}{10a}=\frac{3\times4^2}{10\times4}=1.2\,{\rm m}\\y'&=-{1\over F_{Rx}}\int_{A_x}ypdA_x=-{1\over F_{Rx}}\int_0^Dypwdy=-\frac{\rho gw}{F_{Rx}}\int_0^Dy(D-y)dy\\&=-\frac{\rho gwD^3}{6F_{Rx}}=-\frac{\rho gwD^3}{6}\left(-{2\over{\rho gwD^2}}\right)={D\over3}={4\over3}=1.33\,{\rm m}\end{split}\)

[예제 4] 그림과 같은 탱크내에 깊이 10ft의 물이 들어있다. 탱크 밑부분의 곡면부에 작용하는 합력의 수평, 수직분력의 크기 및 그들의 작용선의 위치를 결정하라.

<풀이> 합력의 식 (3)을 적분하기 위해 θ의 함수로된 p의 표현식을 구한다.

\(p=\gamma h=\gamma(L-y)=\gamma(L-R\cos\theta)\)

또한 원통형 곡면의 미소면적은 dA=wRdθ라 쓸 수 있다. 따라서 \(F_{Rx},\,F_{Ry}\)는 다음과 같다.

\(\begin{align}F_{Rx}&=-\int_ApdA\sin\theta=-\gamma wR\int_0^{\pi\over2}(L-R\cos\theta)\sin\theta d\theta\\&=-\gamma wR\left(L-{R\over2}\right)=-62.4\times10\times4\left(10-{4\over2}\right)=-19.968\,{\rm lbf}\\F_{Ry}&=-\int_ApdA\cos\theta=-\gamma wR\int_0^{\pi\over2}\left(L\cos\theta-R\cos^2\theta\right)d\theta\\&=-\gamma wR\left(L-R{\pi\over4}\right)=-62.4\times4\times10\left(10-4\times{\pi\over4}\right)=-17,119\,{\rm lbf}\end{align}\)

모멘트의 평형식 (4)를 이용하여 합력의 작용선을 찾는다.

\(\begin{split}x'&=-{1\over{F_{Ry}}}\int_AxpdA\cos\theta=-\frac{\gamma wR^2}{F_{Ry}}\int_0^{\pi\over2}\sin\theta\cos\theta(L-R\cos\theta)d\theta\\&=-\frac{\gamma wR^2}{F_{Ry}}\left({L\over2}-{R\over3}\right)=-\frac{62.4\times10\times4^2}{-17,119}\left({10\over4}-{4\over3}\right)=-2.14\,{\rm ft}\\y'&=-{1\over{F_{Rx}}}\int_AypdA\sin\theta=-\frac{\gamma wR^2}{F_{Rx}}\int_0^{\pi\over2}\sin\theta\cos\theta(L-R\cos\theta)d\theta\\&=-\frac{\gamma wR^2}{F_{Rx}}\left({L\over2}-{R\over3}\right)=-\frac{62.4\times10\times4^2}{-19.968}\left({10\over2}-{4\over3}\right)=1.83\,{\rm ft}\end{split}\)