변형률 (Strain)
개요 (Introduction)
본 글에서는 소위 미소 변형률(infinitesmal) 정의에 대해 소개한다. 이것은 잘못된 명칭이다. 미소 변형률 방정식의 정확한 적용을 위해서 작아야될 것은 변형률 자체가 아니라 실제로는 회전이기 때문이다.
수직 변형률 (Normal Strains)
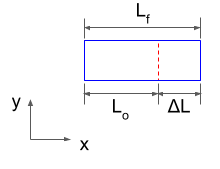
\[\epsilon={\Delta L\over L_o}\]
여기서 각 계측량들은 위의 그림에 정의하였다. 이것은 또한 공학 변형률(Engineering Strain)로 알려져 있다. ΔL이 작을 때는 \(L_o\)는 \(L_f\)에 가까우므로 둘 중에 어느 것이 분모인지 구별은 사실 불필요하다.
전단 변형률 (Shear Strains)
\[\gamma={D\over T}\]
이것은 공학 변형률의 전단 형태이다. 이 상황은 정사각형이 반기계 방향으로 회전하려는 경향이 있으므로 약간의 강체회전(rigid body rotation)을 포함하고 있음에 유의한다. 하지만 지금은 이 문제는 무시한다.
순수전단 변형률 (Pure Shear Strains)
더 바람직한, 하지만 약간 더 복잡한 정의는 다음과 같다.
\[\gamma={\Delta x+\Delta y\over T}\]
\[\Delta x=\Delta y={D\over2}\qquad(\rm 미소 변형률)\]
이것은 두번째 정의를 사용하면서 첫번째 정의 측면으로도 생각할 수 있게 한다.
일반적 정의 (General Definition)
위의 정의들은 모든 변형률이 수직 또는 전단과 같은 간단한 경우에는 유용하다. 그러나 \(\epsilon_x,\,\epsilon_y,\,\epsilon_z,\,\gamma_{xy}\) 등 변형률 성분들이 동시에 존재하는 순간, 취급이 곤란하게 된다. 따라서 보다 일반화된 계산법이 필요하다.
이러한 모순에 대한 답은 ... 미적분에 있다. 이 다양한 변형률을 변위장, u(X)의 편미분으로 정의하는 것이다. 이는 앞의 단순한 경우의 정의법에도 적용할 수 있다.
수직 변형률 (Normal Strains)
수직 변형률 정의는 아래와 같다.
\[\epsilon_x=\frac{\partial u_x}{\partial X}\qquad\epsilon_y=\frac{\partial u_y}{\partial Y}\qquad\epsilon_z=\frac{\partial u_z}{\partial Z}\]
단순 단축 인장(uniaxial stretching)은 다음과 같이 기술된다.
\[x=\left({X\over L_o}\right)L_f\]
그리고 u=x-X 이므로, 윗 식을 대입하면 다음 식을 준다.
\[u_x=\left({X\over L-o}\right)(L_f-L_o)\]
따라서
\[\epsilon_x=\frac{\partial u_x}{\partial X}=\frac{L_f-L_o}{L_o}={\Delta L\over L_o}\]
이므로 요구한 바와 같이 단순인장의 정의식을 재현할 수 있다.
전단 변형률 (Shear Strains)
전단 변형률의 방정식은
\[\gamma_{xy}=\frac{\partial u_y}{\partial X}+\frac{\partial u_x}{\partial Y}\]
전단 변형의 경우 좌표계 상사 방정식(coordinate mapping equation)은
\[\begin{align}x&=X\\y&=Y+XD/T\end{align}\]
그리고 변위장(displacement field)은
\[\begin{align}u_x&=0\\u_y&=XD/T\end{align}\]
전단 변형률은 정의에 따라
\[\gamma_{xy}=\frac{\partial u_y}{\partial X}+\frac{\partial u_x}{\partial Y}=\frac{\partial}{\partial X}(XD/T)+\frac{\partial}{\partial Y}(0)={D\over T}\]
이것은 앞의 단순전단의 경우와 같이 요구된 결과를 준다.
또한 이 방정식의 대칭성은 계산된 전단값이 비회전 조건(no-net-rotation criterion)을 만족한다는 것을 보장한다. 순수전단의 좌표계 상사 방정식은
\[\begin{align}x&=X+Y\Delta x/T\\y&=Y+X\Delta y/T\end{align}\]
그리고 위의 식으로부터 다음 식이 유도된다.
\[\gamma_{xy}={\Delta x+\Delta y\over T}\]
이 역시 요구된 결과를 주고 있다.
2-D 표기법 (2-D notation)
응력처럼, 변형률도 표준 좌표계 변환 원칙(standard coordinate transformation principles)을 따르기 때문에 텐서(tensor)이다. 이는 다음의 여러 형태 중 하나로 쓸 수 있다. 이들은 모두 동일한 표현이다.
\[\boldsymbol\epsilon=\begin{bmatrix}\epsilon_{11}&\epsilon_{12}\\\epsilon_{21}&\epsilon_{22}\end{bmatrix}=\begin{bmatrix}\epsilon_{xx}&\epsilon_{xy}\\\epsilon_{yx}&\epsilon_{yy}\end{bmatrix}=\begin{bmatrix}\epsilon_{xx}&\gamma_{xy}/2\\\gamma_{yx}/2&\epsilon_{yy}\end{bmatrix}\]
\(\gamma_{xy}=\gamma_{yx}\) 이므로, 변형률 텐서는 대칭(symmetric) 이다.(사실 대칭이어야 한다.)
3-D 표기법 (3-D notation)
위의 2-D의 모든 규약은 3-D의 경우 또한 적용된다. 3-D 표기법은 다음과 같다.
\[\boldsymbol\epsilon=\begin{bmatrix}\epsilon_{11}&\epsilon_{12}&\epsilon_{13}\\\epsilon_{21}&\epsilon_{22}&\epsilon_{23}\\\epsilon_{31}&\epsilon_{32}&\epsilon_{33}\end{bmatrix}=\begin{bmatrix}\epsilon_{xx}&\epsilon_{xy}&\epsilon_{xz}\\\epsilon_{yx}&\epsilon_{yy}&\epsilon_{yz}\\\epsilon_{zx}&\epsilon_{zy}&\epsilon_{zx}\end{bmatrix}=\begin{bmatrix}\epsilon_{xx}&\gamma_{xy}/2&\gamma_{xz}/2\\\gamma_{yx}/2&\epsilon_{yy}&\gamma_{yz}/2\\\gamma_{zx}/2&\gamma_{zy}/2&\epsilon_{zz}\end{bmatrix}\]
강체 회전이 제거된 변형률 텐서에서는 \(\gamma_{xy}=\gamma_{yx},\,\gamma_{yz}=\gamma_{zy}\,{\rm 및}\,\gamma_{zx}=\gamma_{xz}\)의 관계가 있다. 이 또한 대칭 텐서의 결과를 준다.





댓글
댓글 쓰기