보의 굽힘 (Beam Bending)
본 글은 고전적 보의 굽힘 이론(classical beam being theory)에 대하여 복습한다. 이는 거의 모든 구조 설계와 해석에 있어서 중요한 고려 대상이다. 다소 명확하지는 않지만, 기둥의 좌굴(column buckling)과도 또한 관련이 있다.
곡률 반경 (Radius of Curvature)보의 굽힘에 있어서 곡률 반경은 기본이 되므로 복습하도록 한다. 곡률 반경은 통상 그리스 문자 ρ로 나타내고, 그래프의 일부분 도로의 커브, 또는 대부분 경로의 일부와 같은 곡률을 갖는 원의 반경으로 생각할 수 있다. 경로가 직선이면, ρ는 무한대이고 날카로운 곡선이면 매우 작을 것이다.
곡률 반경에 대한 수학적 표현을 알아 본다. 위의 그림과 같이 임의의 함수 y=f(x)를 생각한다. 호의 길이 s=ρθ이고, 여기서 θ는 호의 각도이다. 미소 증분은 ds=ρdθ이고 양변을 dx로 나누면
\[\rho\frac{d\theta}{dx}=\frac{ds}{dx}\]
이제 dθ/dx와 ds/dx에 대한 표현이 필요하므로 먼저 dθ/dx는 다음 관계를 상기하면
\[\tan\theta=\frac{dy}{dx},\ \text{따라서}\ \theta={\rm Tan}^{-1}(y')\]
dθ/dx를 얻기 위해 x에 관해 미분하면 (미분과정은 링크를 참조한다.)
\[\frac{d\theta}{dx}=\frac{y''}{1+(y')^2}\]
\[ds^2=dx^2+dy^2\]
양변을 dx로 나누고 제곱근을 취하면
\[\frac{ds}{dx}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}=\sqrt{1+(y')^2}\]
이들을 앞의 식에 대입하고 정리하면 유명한 다음 식을 얻는다.
\[{1\over\rho}=\frac{y''}{\left\{1+(y')^2\right\}^{3/2}}\]
수많은 역학적 작용에 있어서 굽힘이 관련되어 있지만, 대부분 미소 영역에 한정되어 있다는 것은 흥미롭다. 이러한 경우 최선의 접근법으로써 보의 길이 방향으로 x축을 정의하면 y방향 처짐(deflection)과 기울기(slope) y'은 둘 다 미소할 것이다. 만약 y'≪1 이면, y'은 위의 식에서 무시할 수 있다. 이는 훨씬 간단한 표현식을 준다.
\[{1\over\rho}\approx y''\]
3-D 곡률 반경 (3-D Radius of Curvature)
매우 유용한, 그리고 일반적인 3-D 곡률 반경의 표현은
\[{1\over\rho}=\frac{\bf|v'+v''|}{|{\bf v'}|^3}\]
여기서 v는 v=v(x(t), y(t), z(t))와 같이 매개변수로 정의된 벡터이다. v'는 1차 도함수, v''는 2차 도함수, 그리고 \(|\cdots|\)는 해당 벡터의 길이를 나타낸다.
굽힘 변형률 (Bending Strains)
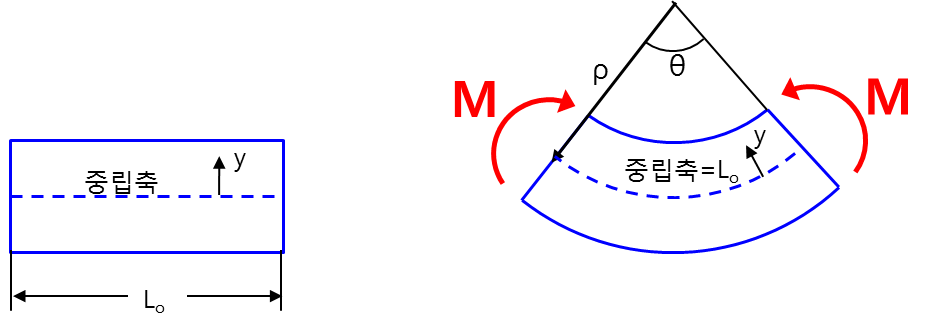
아래 그림과 같이 초기 길이 \(\rm L_o\)의 보의 굽힘을 생각한다. 보는 유한한 두께를 가지므로 두께 방향 위치에 따라서 늘음 또는 수축이 다른 값으로 발생할 것이다. 보의 외각은 중앙으로부터 가장 멀리 있으므로 가장 많이 늘어난다. 수학적으로, 모든 부위는 같은 각도 θ 만큼 굽힘이 일어나지만, 두께 방향으로 ρ는 변하고, 따라서 ρθ 및 L도 변한다.
먼저 \(\rho\theta=L_o\)를 만족하는 ρ를 구한다. 여기서 ρ는 계산된 값이고 θ와 \(L_o\)는 주어진 값이다. 또한 \(L_o\)는 초기, 변형 전 길이이다.
\[L=(\rho-y)\theta\]
\(L_o=\rho\theta\) 이므로, 이제 \(\epsilon_x\)는 다음과 같이 표현된다.
\[\epsilon_x=\frac{L-L_o}{L_o}=\frac{(\rho-y)\theta-\rho\theta}{L_o}=-{y\over\rho}\]
이것이 보의 변형률에 대한 중요 결과이다. 이는 중립축인 y=0에서의 변형률이 영이라는 것을 보여주고 중립축으로부터 거리만큼 선형으로 변화한다. 만약 보의 두께가 두꺼우면 y는 큰 값을 취할 것이고, 얇으면 반대일 것이다. 이것은 왜 두꺼운 보가 얇은 보 보다 큰 굽힘 강성을 갖는 지에 대해 설명한다.
또한, 분모의 곡률 반경은 많은 굽힘 효과들을 설명한다. 보가 굽힘을 받지 않을 때, ρ는 무한대가 되고, 변형률은 자연히 영이 된다. 위의 방정식은 보가 굽혀짐에 따라, ρ는 감소하고 변형률은 증가함을 보여준다.
마지막으로, 이 변형률은 수직 변형률(normal strain)이고, 사실 보의 길이 방향을 따라, 횡방향(longitudinal)이다. 통상적으로 보의 길이 방향은 x축이므로, \(\epsilon_x\) 이다.
굽힘 응력 (Bending Stress)
변형률에 표현으로부터 응력은 간단히 유도된다. 변형률 식에 탄성계수 E를 곱하면 \(\sigma_x\)를 얻는다.
\[\sigma_x=-{Ey\over\rho}\]
위의 과정은 매우 단순하지만, 사실 단순함을 위하여 무시된 것으로부터 깊은 의미를 가진다. 후크의 법칙 글에서 각 수직 응력 성분은 모든 3개의 변형률 성분에 의존한다는 점을 상기해 보자. 하지만 여기서는, 응력을 얻기 위해 단순히 변형률에 E만을 곱하였다. 이 과정에서 보에 횡방향 하중/응력이 존재하지 않는다는 중요한 가정이 있는 것이다. 이러한 경우에는 단축 인장처럼 \(\sigma_x=E\epsilon_x\)이 성립한다. 이는 대부분의 보가 길이에 비해 얇기 때문에 적용될 수 있다.
평판의 굽힘 (Bending in Plates)
평판에서는 위의 과정이 더 복잡해진다. 왜냐하면 길이에 비해서 두 방향이 아닌, 한 방향으로 얇기 때문이다. 얇지 않은 방향으로는 인장과 연계된 포아송 효과(Poisson Effect)에 따라 저항하므로 다음 식이 유도된다.
\[\sigma_x=\frac{E}{(1-\nu^2)}\epsilon_x\]
여기서 υ는 재료의 포아송 비이다. 위의 식으로부터 동일 변형률 조건에서 전형적인 단축 인장보다 더 큰 응력이 작용함은 명백하다.
굽힘 모멘트와 응력 (Bending Moments and Stress)
\[M_z=\int_Ar\times dF=-\int_Ay\sigma_xdA=-\int_Ay\left(-{Ey\over\rho}\right)dA={E\over\rho}\int_Ay^2dA={EI_{zz}\over\rho}\]
위의 식에서 적분 \(I_{zz}\)는 매우 중요하며 완전히 기하학적인 값이다. 이것은 단면의 관성 모멘트(moment of inertia) \(I_{zz}\)라 불리운다.
\[I_{zz}=\int_Ay^2dA\]
이제 위의 굽힘 모멘트와 응력의 방정식으로부터 둘 다 E/ρ가 포함된 것을 알 수 있다. 각 방정식을 이 비(比)에 대하여 풀면
\[{E\over\rho}={M_z\over I_{zz}}=-{\sigma_x\over y}\]
\(\sigma_x\)에 대해 정리하면 기계공학에서 가장 잘 알려진 식을 얻는다.
\[\sigma_x=-{M_zy\over I_{zz}}\]
3-D 굽힘 (3-D Bending)
\[\epsilon_x={z\over\rho_y}-{y\over\rho_z}\]
응력을 얻기 위해 E를 곱한다.
\[\sigma_x={Ez\over\rho_y}={Ey\over\rho_z}\]
굽힘 모멘트 \(M_y\)는 단면에 작용하는 응력을 모멘트 팔 z에 대하여 적분하면 계산된다.
\[M_y=\int_Az\sigma_xdA={E\over\rho_y}\int_Az^2dA-{E\over\rho_z}\int_AyzdA={E\over\rho_y}I_{yy}-{E\over\rho_z}I_{yz}\]
다른 굽힘 모멘트 \(M_z\)는 단면에 작용하는 응력을 모멘트 팔 y에 대하여 적분하면 계산된다.
\[M_z=\int_Ay\sigma_xdA={E\over\rho_z}\int_Ay^2dA-{E\over\rho_y}\int_AyzdA={E\over\rho_z}I_{zz}-{E\over\rho_y}I_{yz}\]
위의 식들은 다음과 같이 행열 형태로 간단히 쓸 수 있다.
\[\left\{\begin{matrix}M_y\\M_z\end{matrix}\right\}=\begin{bmatrix}I_{yy}&-I_{yz}\\-I_{yz}&I_{zz}\end{bmatrix}\left\{\begin{matrix}E/\rho_y\\E/\rho_z\end{matrix}\right\}\]
이로부터 관성 모멘트는 사실 텐서임을 알 수 있다.
이 방정식을 모멘트의 함수로 곡률 반경을 얻기 위해 변환하는 것이 더 유용한다. 이렇게 하면 다음 식을 준다.
\[\begin{Bmatrix}E/\rho_y\\E/\rho_z\end{Bmatrix}={1\over I_{yy}I_{zz}-I_{yz}^2}\begin{bmatrix}I_{zz}&I_{yz}\\I_{yz}&I_{yy}\end{bmatrix}\begin{Bmatrix}M_y\\M_z\end{Bmatrix}\]
위의 식을 앞의 응력에 관한 식의 \(E/\rho_y\) 및 \(E/\rho_z\)에 대립하면 다음 식을 얻는다.
\[\sigma_x={1\over\rm det(\bf I)}\begin{Bmatrix}-y&z\end{Bmatrix}\begin{bmatrix}I_{yy}&I_{yz}\\I_{yz}&I_{zz}\end{bmatrix}\begin{Bmatrix}M_z\\M_y\end{Bmatrix}\ \text{여기서}\ {\rm det(\bf I)}=I_{yy}I_{zz}-I_{yz}^2\]
마지막으로, \(I_{yz}=0\) 이면 다음과 같이 매우 간단하게 된다.
\[\sigma_x={M_yz\over I_{yy}}-{M_zy\over I_{zz}}\]







E/p 비에 대해 푼 식에서 굽힘 응력과 y의 비가 반대로 되어있습니다.
답글삭제수정했습니다. 감사합니다.
삭제