동적 재료 특성 (Dynamic Material Properties)

고전 동적 재료시험은 시편에 사인파 하중의 적용과 그의 변위 응답을 기록하는 것이다. 하중과 변위 데이터는 응력과 변형률 주기를 계산하기 위하여 사용된다. 변형률 진폭에 대한 응력 진폭의 비를 동적 탄성률(dynamic modulus)이라 한다. 전단 하중에 대해서는 통상 기호, G가 사용된다. 응력 입력과 변위 반응의 위상차, δ 또한 계측되며 tan(δ)로 나타낸다. 이들 변수들의 여러가지 조합을 변형률 진폭, 온도 그리고/또는 진동수에 대하여 선도로 표시한다.

정의 (Definitions)

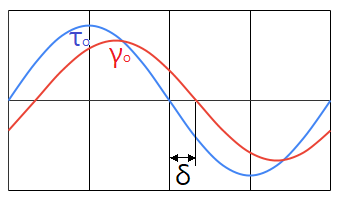
전단응력 진폭, \(\tau_o\), 전단변형률 진폭, \(\gamma_o\), 및 위상차, \(\delta\)는 서로 다른 물성 정의를 나타내기 위하여 여러 방법으로 조합된다. 가장 보편적인 방법은 간단히 변형률에 대한 응력비로 나타낸는 동적 탄성률(dynamic modulus), G* 이다. 응력에 대한 변형률의 비는 동적 컴플라이언스(dynamic compliance), J*가 된다.

\[G*={\tau_o\over\gamma_o}\qquad J*={\gamma_o\over\tau_o}\]

명백히 G*=1/J* 이고 역(逆)도 참이다. 나머지 기본적인 양은 종종 "탄젠트 델타(tan δ)" 또한 때때로 "손실 탄젠트(loss tangent)"로 불리우는 위상차, tan(δ) 이다.

동적 탄성률의 동상(同相, in-phase)성분과 이상(異相, out-of-phase) 성분은 각각 저장 탄성률(storage modulus)과 손실 탄성률(loss modulus)이라 한다.

저장 탄성률    G'=G*cos(δ)
손실 탄성률    G"=G*sin(δ)

위의 식으로부터 명백히 tan(δ)는 G'에 대한 G"의 비율이다.

\[\tan(\delta)={G"\over G'}\]

동적 컴플라이언스의 동상(同相, in-phase)과 이상(異相, out-of phase)성분은 각각 저장 컴플라이스언스(storage compliance)와 손실 컴플라이언스(loss compliance)라 한다.

저장 컴플라이언스     J'=J*cos(δ)
손실 컴플라이언스     J"=J*sin(δ)

그리고 또한, tan(δ)는 J'에 대한 J"의 비율임은 명백하다.

\[\tan(\delta)={J"\over J'}\]

변형률 의존성 (Strain Dependence)

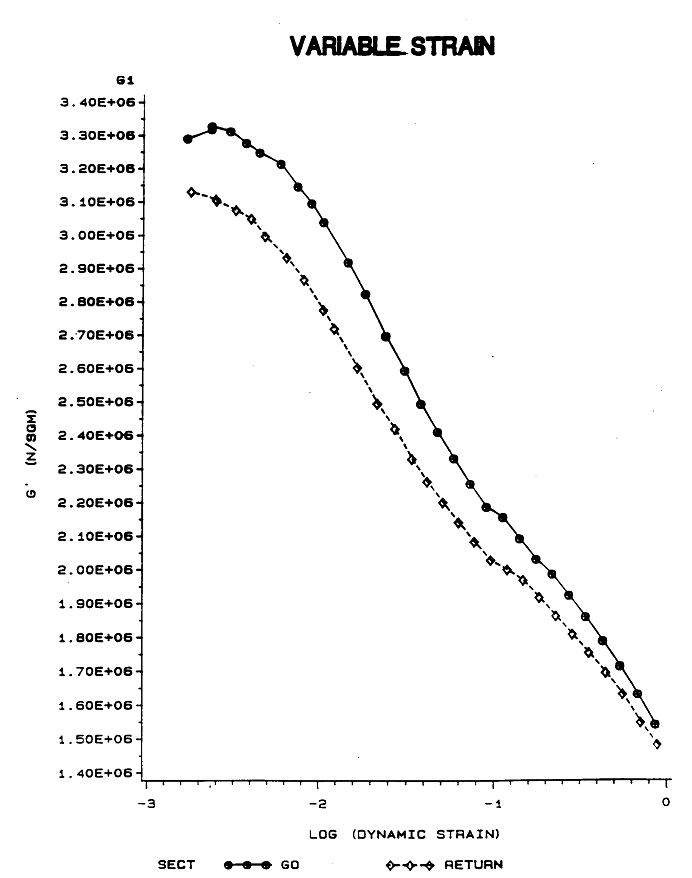
아래 선도는 어느 고무 시편의 시험 데이터이다. 무니-리블린 모델의 단축인장 시험 데이터와 같이 고무의 강성은 변형률 진폭이 커질 수록 감소한다. "GO" 라벨의 곡선은 입력하중이 시간에 따라 증가하는 시험의 일부이다. "RETURN" 라벨의 곡선은 입력하중이 시간에 따라 감소하는 시험의 일부이다. 이 둘 간의 차이는 멀린스 효과(Mullins Effect)라 불리운다.

다음은 동일 고무시편의 위상차(phase lag) 시험 데이터이다.

물성 요약 (Material Summary)

다음은 고무 물성의 동적 특성을 요약해서 보여준다. 온도와 진동수는 반대방향으로 증가함에 유의한다.

시간 온도 등가 (Time Temperature Equivalence)

2차 세계대전 경, 윌리엄즈(Williams), 랜델(Landel)과 페리(Ferry)는 고분자재료(polymer)의 흥미로운 성질을 보고하는데 그것은 시간-온도 등가성(time-temperature equivalence)이다. 그들은 고분자재료의 기준 온도 및 진동수에서의 동적물성은 다른 온도와 진동수 조합에서도 재현될 수 있으며 처음 조합의 단일 방정식으로 예측할 수 있음을 밝혀 내었다. 그 방정식은 오늘날 WLF 방정식 또는 WLF 변환으로 알려져 있다.

시간-온도 등가성의 의미는 고분자재료의 적절히 정해진 저온 및 저진동수 조합에서 강성(stiffness)과 이력현상(hysteresis)은 주어진 고온 및 고진동수 조합에서의 경우와 같다는 것이다.

이러한 성질은 시험 관점에서 매우 유용하다. 왜냐하면 수천 헤르츠의 진동 시 재료의 점탄성을 저진동수와 매우 낮은 온동에서 시험함으로써 예측할 수 있기 때문이다. (이것은 종종 정지마찰력 연구(traction studies) 시 행해진다.)

WLF 변환 (WLF Transforms)

WLF 방정식은 많은, 유사한, 하지만 약간 다른 형태로 쓰여진다. 여기서 주어진 식은 일반 형태의 특수한 경우의 하나일 뿐이다.

\[\log_{10}\left({f_1\over f_0}\right)=\frac{-C_1(\theta_1-\theta_0)}{(C_2+\theta_0)(C_2+\theta_1)}\ \text{여기서}\ \begin{cases}\theta_0=T_0-T_g\\\theta_1=T_1-T_g\end{cases}\]

통상적인 상수값은 \(C_1=900\)과 \(C_2=51.6\) 이다. (\(T_g\) : 글라스 천이온도)

계수, \(C_1\)과 \(C_2\)는 WLF 방정식을 시험테이터에 가장 적합한 곡선(curve fitting)으로 만드는 값으로 취득한다. 적용예에 따른 이들의 변동은 미미하다. 요컨데 다른 조건의 시험에서는 약간 다른 값을 가질 수 있으나 상당한 불확실성이 있으므로 무시할 수도 있다.

전반적으로 WLF 변환은 수십 헤르츠의 진동수와 (Tg, Tg+100℃) 온도구간에서 완벽하지는 않아도, 꽤 잘맞는 편이다. WLF 변환은 아래와 같이 \(\theta_1\)에 대한 식으로 나타내는 것이 좀 더 실용적이다.

\[T_1-T_g=\frac{C_1\theta_0-C_2(C_2+\theta_0)\log_{10}(f_1/f_0)}{C_1+(C_2+\theta_0)\log_{10}(f_1/f_0)}\]

위의 다중응력(multi-stress) 시험결과를 생각하자. 이 그래프는 광범위한 온도에서 10 Hz 진동 시의 물성을 제공한다. 임의로 10Hz, 70℃ 및 0.035 kg/mm² 응력 수준에서 출발한다(그래프에서 실선). 이들 조건에서 tan(δ)=0.17 이다. 70℃, 100Hz 조건에서 tan(δ)를 구하기 위해서 다음 값들을 이용하면

\[\begin{align}&C_1=900\qquad\ \ \ \ \,T_0=70^\circ C\\&C_2=51.6\qquad\ \ \ \ f_0=10{\rm Hz}\\&T_g=-20^\circ C\qquad f_1=100{\rm Hz}\end{align}\]

\[T_1=-20+\frac{(900)(90)-51.6(51.6+90)\log_{10}(100/10)}{900+(51.6+90)\log_{10}(100/10)}=51^\circ C\]

51℃를 얻는다. 즉, 51℃ 및 10Hz 조건이면 tan(δ)=0.2 이다. 그러므로, \(T_1=70^\circ C\) 및 100Hz 조건에서, tan(δ)는 동일한 0.2가 되어야 한다.

출처 http://www.continuummechanics.org