재료물성과 타이어 거동 (Material Properties & Tire Behavior)

소개 (Introduction)

본 글에서는 타이어 성능 측면에 영향을 미치는 고무 물성에 대해 알아본다. 특히, 열발생, 작동온도, 구름저항(rolling resistance) 및 견인성능(traction performance)에 대한 고무 탄성률(rubber modulus)과 위상차(phase lag)의 영향에 대해 논한다.

배경 (Background)

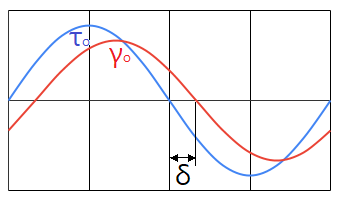
많은 타이어 성능 측면의 핵심은 고무 복합재에 존재하는 이력감쇠(hysteretic damping)로 인한 구름 열발생률(rate of heat generation)이다. 이력감쇠의 결과로 아래 그림과 같이 응력과 변형률 주기 간의 위상차가 발생한다.

과도(transient) 응력과 변형률 신호는 다음과 같이 표현된다.

\[\sigma(t)=\sigma_o\sin(wt)\qquad\text{and}\qquad\epsilon(t)=\epsilon_o\sin(wt-\delta)\]

위의 식을 회전 당 열발생을 계산하기 위하여 다음 방정식에 대입한다.

\[W=\int\sigma(t)d\epsilon(t)=\int\sigma_o\sin(wt)d\left\{\epsilon_o\sin(wt-\delta)\right\}=\sigma_o\epsilon_o\int_o^{2\pi}\sin(wt)\cos(wt-\delta)\]

삼각함수 항등식을 활용하여 정리하면

\[W=\sigma_o\epsilon_o\int_0^{2\pi}(\cos\delta\sin x\cos x+\sin\delta\sin^2x)dx=\pi\sigma_o\epsilon_o\sin\delta\]

위의 식은 주기 당, 즉, 타이어 한 회전 당 기계적 일의 손실(mechanical energy loss)을 나타낸다. 이 기계적 에너지 손실은 열역학 제1법칙에 따라 열발생과 같아야 한다: \(W_{\rm lost}=Q_{\rm generated}\) 그리고 타이어 회전 진동수 f를 곱하면 열발생률 dQ/dt를 구할 수 있다.

\[\dot{Q}=f\pi\sigma_o\epsilon_o\sin\delta\]

물론, 이것은 단순화된 식이다. 실제 타이어는 3-D 변형이 발생하고 변형이력은 단순 사인파는 아니다. 하지만 경향성은 맞다. 열발생률은 (i) 타이어 회전수 f, (ii) 재료 위상차 δ, 및 (iii) 응력과 변형률 진폭의 곱 \(\sigma_o\epsilon_o\)에 비례하여 증가한다.

하중법에 의한 구름저항력 측정 (Rolling Resistance Calculation by Force Method)